【円の性質】円周角の角度の求め方の3つのパターン
円周角の角度の求め方は3パターン??
やあ,Dr.リードだぞいっ!!
円周角の定理は頭に入ったよな!!
だよな!
円周角の定理はおぼえるだけじゃだめだ。
実際に、いろんな問題を解いてみることが大事なんだ。
円周角の問題を解くコツは、
でっかく自分で図をかいてみること。
問題集の円なんて、小さすぎて見にくいだろ??
これだと考えにくいから、
ノートや別の紙にお皿くらいでっかく描いて考えてみるといいな。
そうそう。でっかくでっかく。
中華料理のターンテーブルみたいにさ、くるくる回しやすいだろ?

今日は、テストにでやすい円周角の求め方を3パターン紹介していくぞ。
- 円周角の定理を使うだけの問題
- 補助線をひく問題
- 中心角と円周角から他の角を計算する問題
円周角の求め方は意外とシンプルでわかりすいんだ。
円周角の求め方1. 「素直に円周角の定理を利用するパターン」
まずは、円周角の定理を使った求め方だね。
円周角の定理は、
- 1つの弧に対する円周角の大きさは、その弧に対する中心角の半分である。
- 同じ弧に対する円周角の大きさは等しい。
の2つだったよな?
忘れたら円周角の定理の記事で復習しような。
それじゃあ円周角の問題を解いていくぞ。
円周角の問題1.
次の角xを求めなさい。
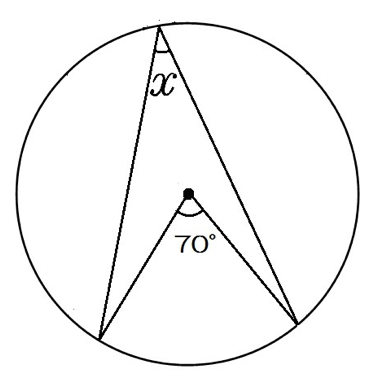
この問題では円周角の定理の、
1つの弧に対する円周角の大きさは、その弧に対する中心角の半分である。
を使っていくぞ。
円周角は中心角の半分。
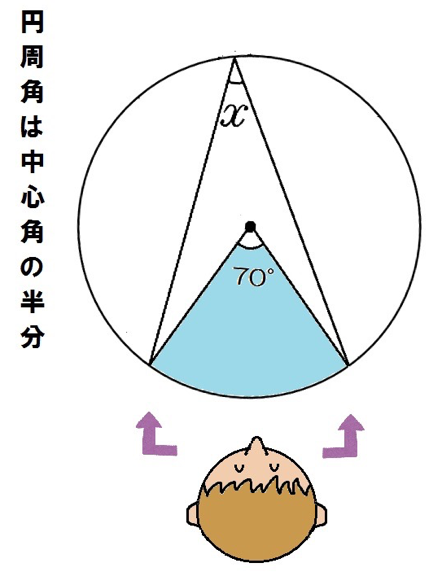
だから、xは35°だ。
円周角の問題2.
次の角xを求めなさい。
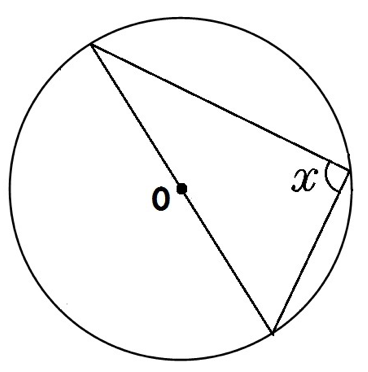
この円周角の求め方もさっきと同じ。
同じ孤に対する円周角は中心角の半分。
この円は円の半分だから、中心角は180°。
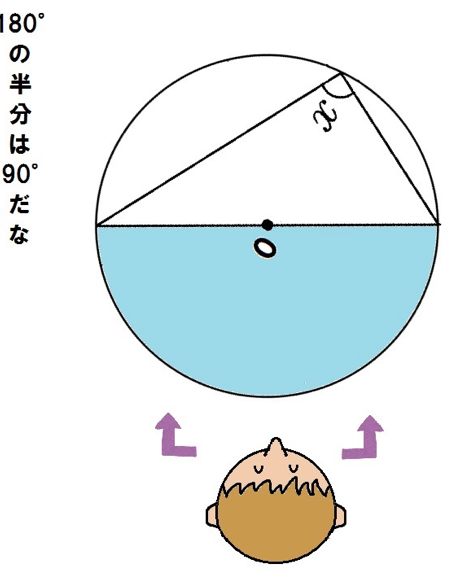
よって、円周角のxは90°。
これも基本通り。
直径に対する円周角は90° はよくでてくるぞ。
円周角の問題3.
次の角xを求めなさい。
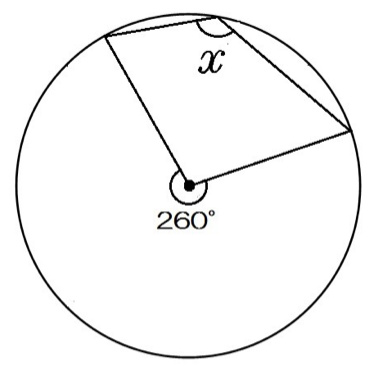
この問題も同じさ。
中心角が260度だから、円周角xはその半分で
130度。
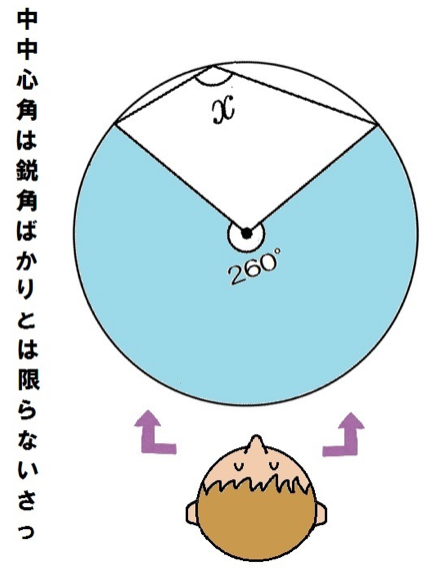
円周角の問題4.
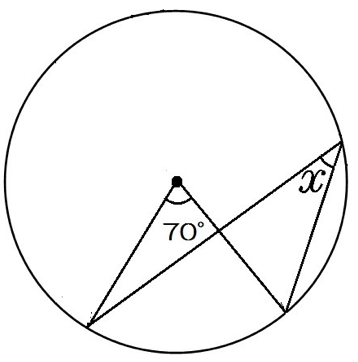
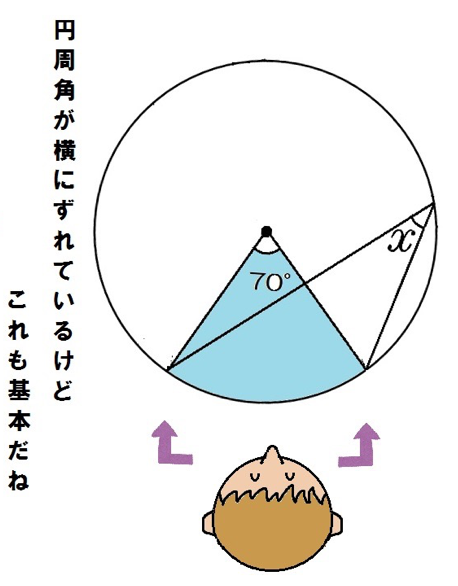
円周角の頂点が中心角からずれてるパターン。
基本の求め方は同じだぞ。
円周角は中心角70°の半分だから35°だ。
円周角の求め方5.
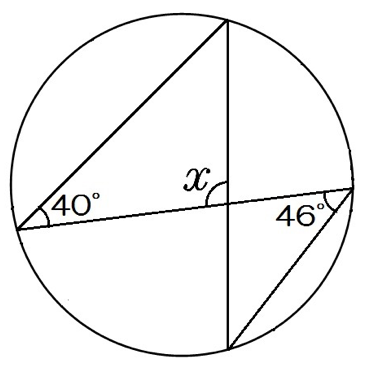
リボンタイプの問題っておぼえておくといいよ。
中心角はかかれてない。
この問題では、
同じ弧の円周角はどこも同じってことを利用する。
角xは、
180-40-46=94°
になるね。
円周角の求め方6.
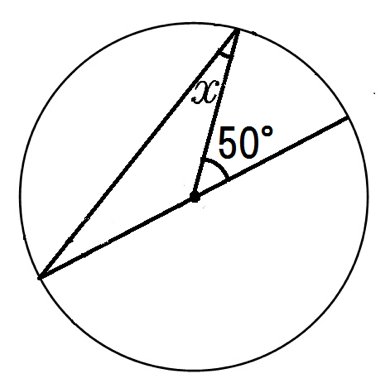
げっ、円周角じゃないとこきかれてるじゃん。
でも中心角を頂角にする三角形が「二等辺三角形」ってことを利用すると・・・
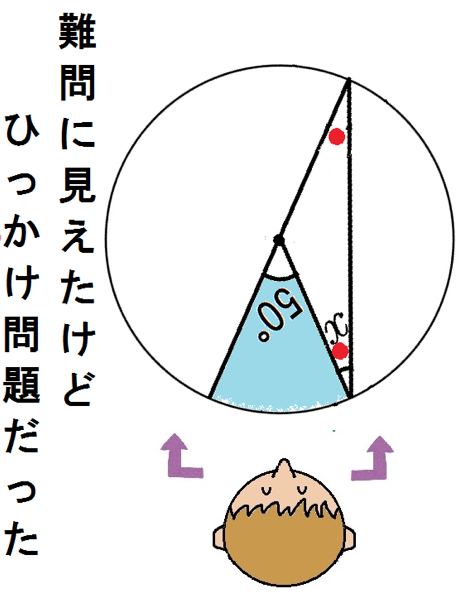
つまり50°の半分、25°が円周角だね。
二等辺三角形の底角は等しいからxも25°。
円周角の求め方2. 補助線を引くパターン
次はちょっと難しい問題。
補助線を引かないと円周角が求められないやつだ。
円周角の問題7.
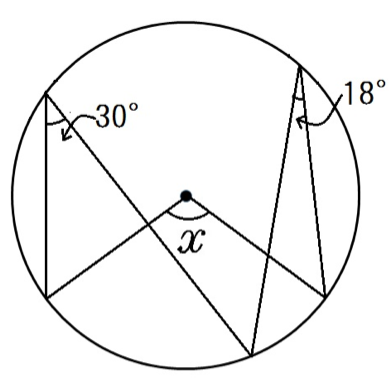
さあ、補助線を引くぞ。
中心角を2つに分けられる補助線を引けばいいんだ。
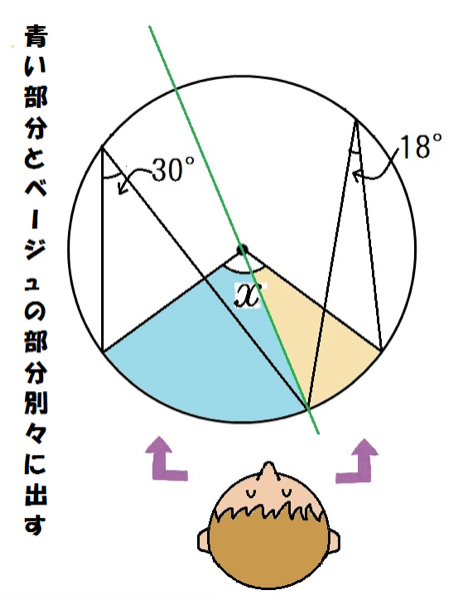
補助線さえ引けたら,円周角の問題が2つドッキングしてるだけなんだよね。
青いほうが円周角の2倍だから60°。
ベージュのほうが円周角の2倍で36°。
合計でxは96°だ。
補助線引けないと手も足も出ないが、コツさえつかめばだいじょうぶ。
円周角の問題3. 「中心角・円周角から他の角を出すパターン」
最後は、中心角・円周角出したその先がある問題。
もうひと踏ん張りのパターンだ。
円周角の問題8.
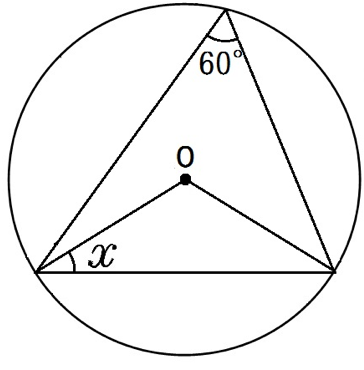
円周角60°ってことは、中心角は2倍の120°。
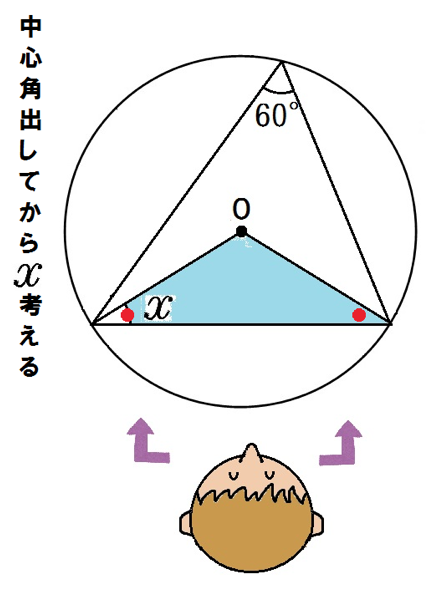
水色の三角形は二等辺三角形だから底角は等しい。
よって、底角のxは、
(180-120)÷2=30
になるぞ。
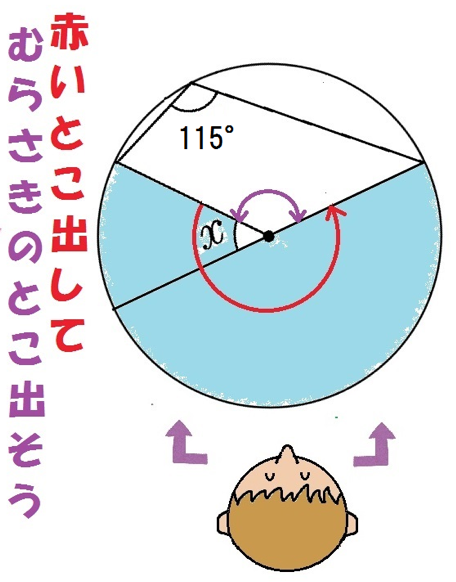
円周角の問題9.
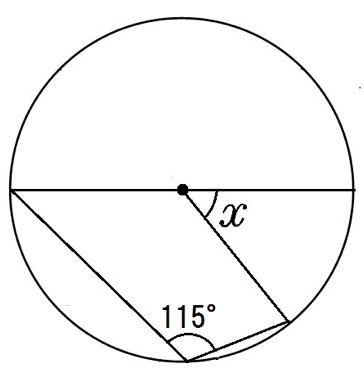
円周角115°だから、赤い中心角は2倍の230°。
紫のとこは、
360-230=130°
だから、求めるxは、
180-130=50°
うんうん。
みるからに50°だ。
まとめ:円周角の求め方はパズルみたいなもん!
円周角の求め方はパズルみたいだね。
変に難しく考えなくて大丈夫。
あとは円の見方を変えたりするぐらいかな。
テストによく出てくるから復習しておこうぜ。
じゃ、おつかれさん。
一緒に中華料理でも食うかな!
Dr.リード




