【中2数学】式の値を求める3つのステップ
中2数学の「式の値」の問題がむずい??
こんにちは!この記事をかいているKenだよ。カラオケもいいね。
中2数学でh「式の値」っていうやっかいなヤツがでてくる。
「式の値」の問題って、
文字式の中の「文字」に数字をいれたときの値を求める
っていうやつなんだ。
文字に数字をいれて計算するだけ!
慣れれば簡単だからガンガン点をとっていこう。
今日は中2数学ででてくる、
「文字が2つ以上登場する」式の値の問題
を解説していくよ。
よかったら参考にしてみて。
中2数学の「式の値」がわかる3ステップ
さっそく「式の値」の解き方をみていこう。
つぎの例題をといてみよう!
a = 3/2、b = -2/17のとき、次の式の値を求めなさい。
(8a + 3b) -2(3a-7b+1)

この手の問題は3ステップでちょちょいのチョイさ。
Step1. 分配法則で()をはずす!
文字式を簡単にしてあげよう!
チョー簡単な式はそのままでいいんだけど、
()のついた式はもう少しシンプルにしちゃおう。
例題の文字式をみると、
(8a + 3b) -2(3a-7b+1)
って感じで()で文字式が太っているよね??
とてもじゃないけどスリムなんかじゃない。
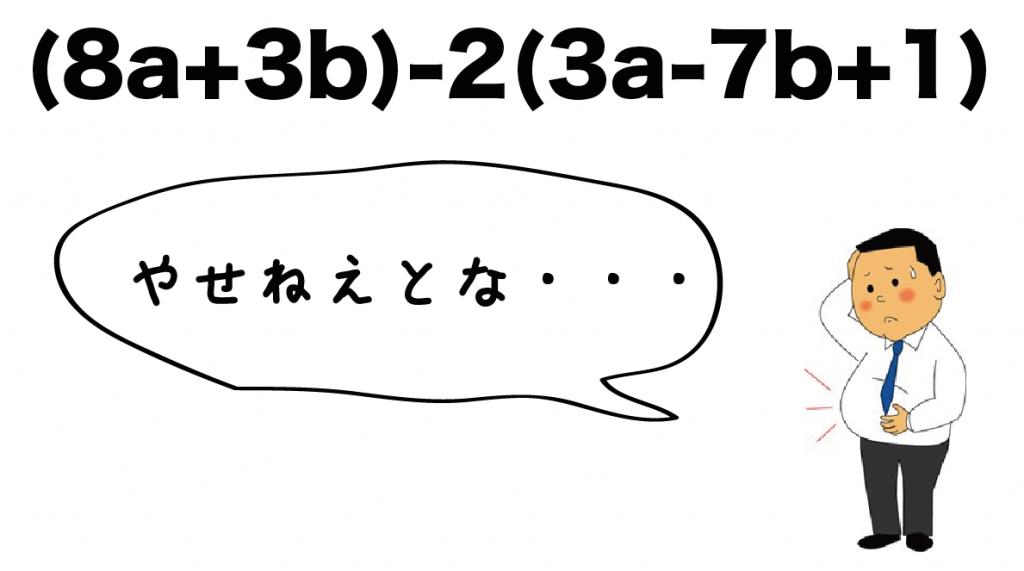
(8a + 3b) -2(3a-7b+1)
をスリムにするために分配法則をつかってあげよう。
すると、
(8a + 3b) -2(3a-7b+1)
= 8a + 3b -6a + 14b -2
になるね!
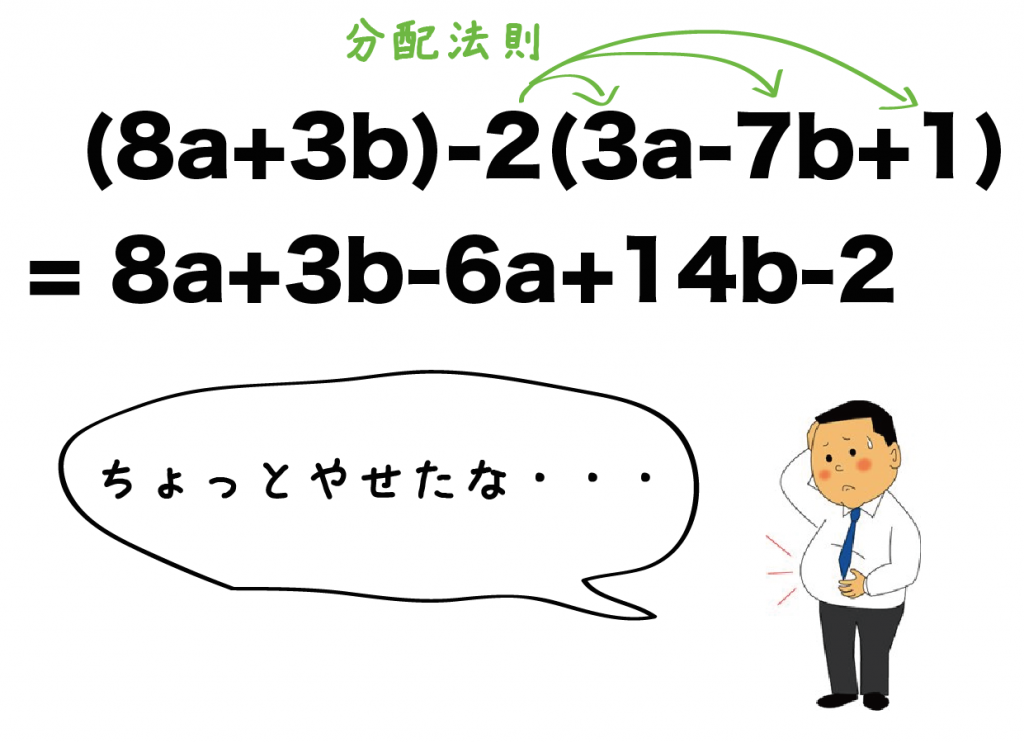
どう??だいぶスリムになったよね?。
Step2. 同類項をまとめる!
文字式の()をはずしただけじゃまだスリムじゃない。
式は横に長いし、どうにかしてあげたくなるよね?。
つぎはもっとシンプルにするために、
同類項をまとめる
っていう荒技で勝負してみよう。
例題でちょっと簡単にした、
8a + 3b -6a + 14b -2
という式にはつぎの3種類の項があるよね?
- a
- b
- 数字
同じ文字の項は係数をたしてみよう。

すると、
2a +17b -2
って感じで文字式がスリムになったでしょ??
Step3. 数字を代入する!
最後に文字に数字を代入してみよう。
どんな数字を入れればいいのか
ってことは問題にかいてあるよ。
この例題では、
- a = 3/2
- b = -2/17
って問題で指定されているよね?
こいつらをStep2で計算した超スリムな文字式に代入してあげよう。
すると、
2a +17b -2
= 2 × 3/2 + 17×(-2/17) -2
= 3 + (-2) -2
= -1
っていう式の値が求まるね!
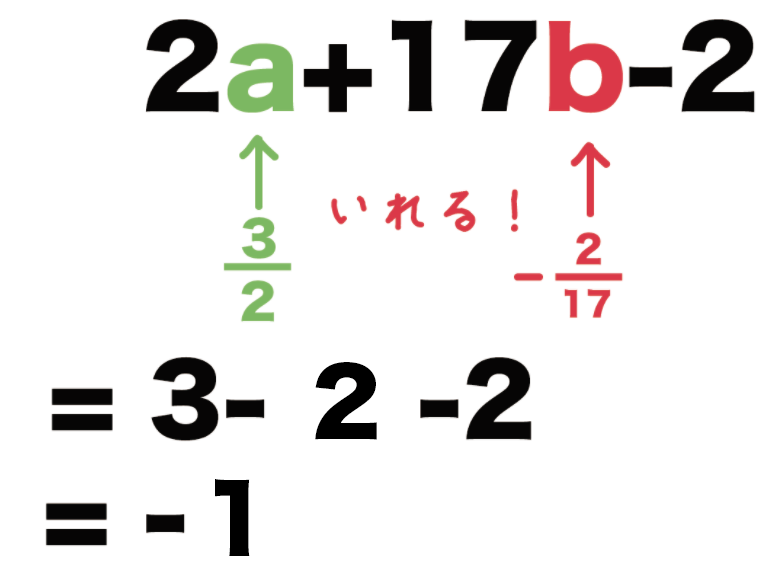
おめでとう。これで「式の値」もマスターしたね。
まとめ:「式の値」を求める前には文字式をスリムに!
式の値を求める前には必ず、
文字式をできる限りカンタンにする
ってことを忘れずにね!
これなら焦らずに式の値を計算できるはず!
テスト前にもう一度復習してみてね。
そんじゃねー
Ken