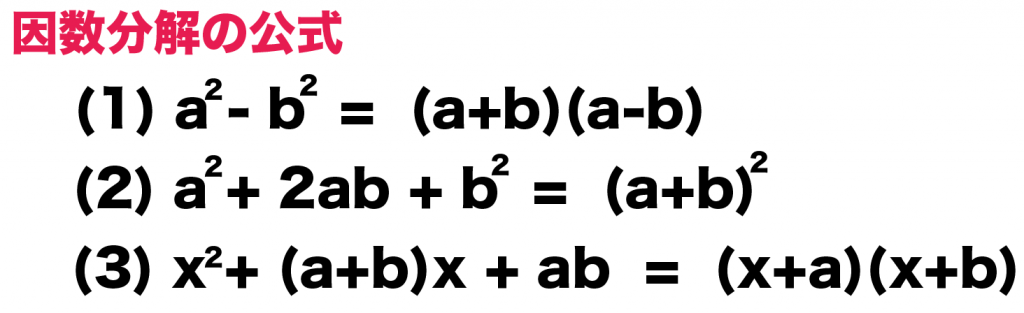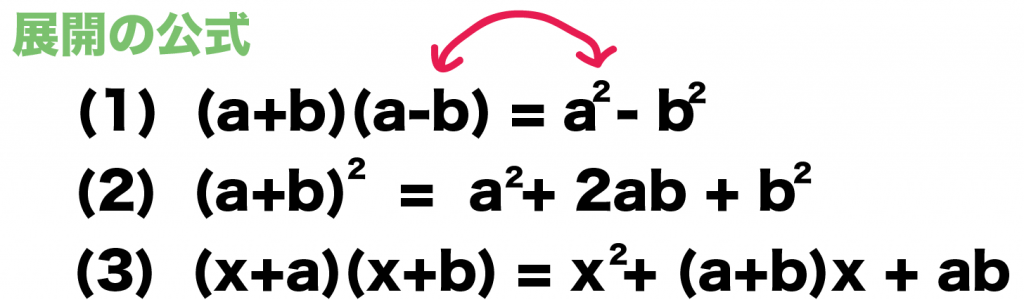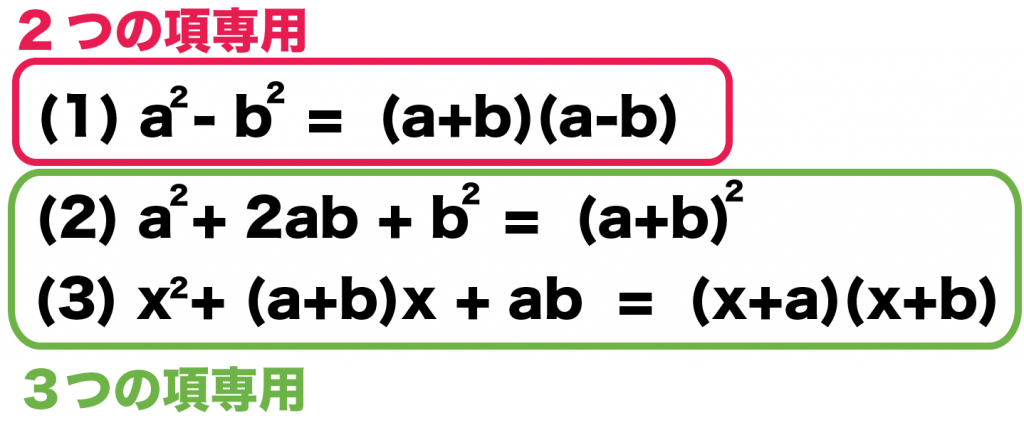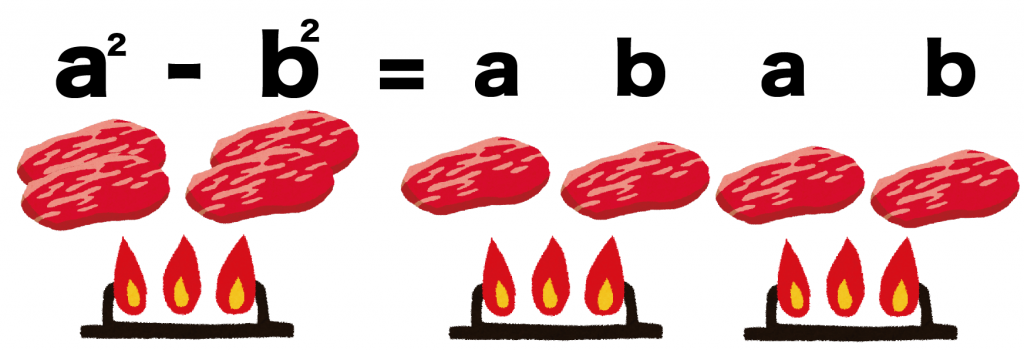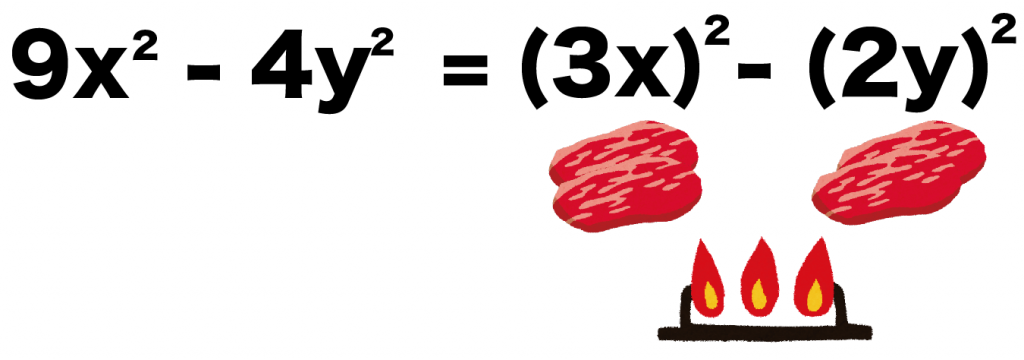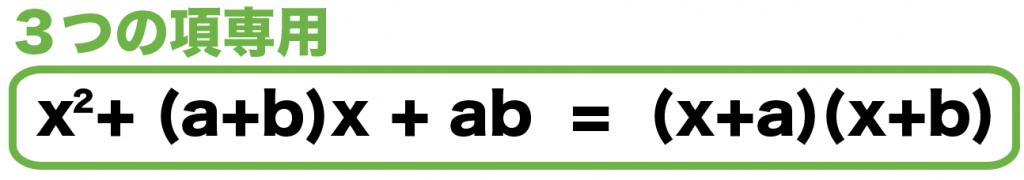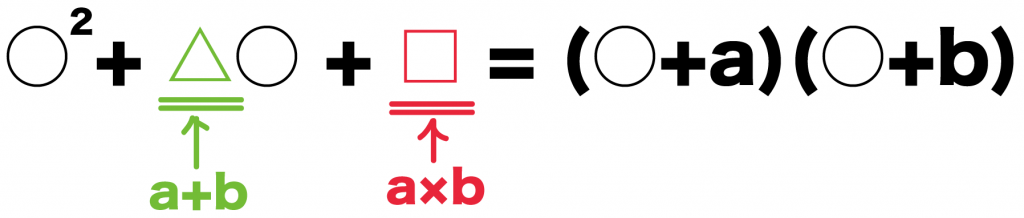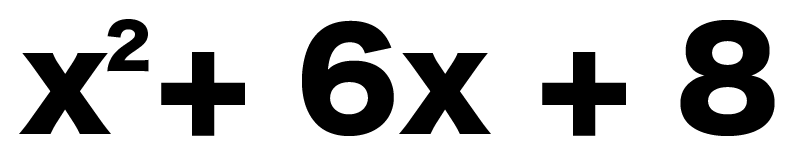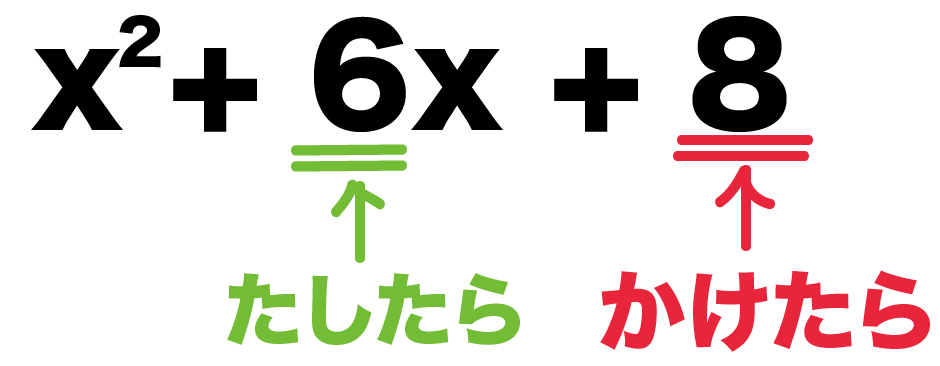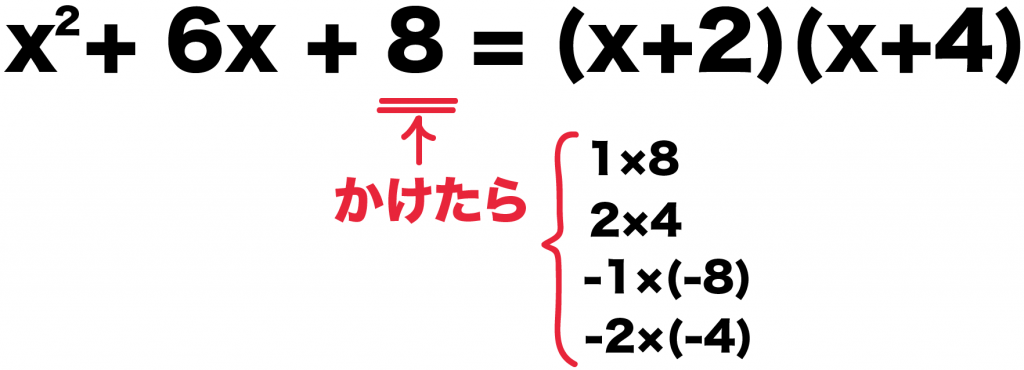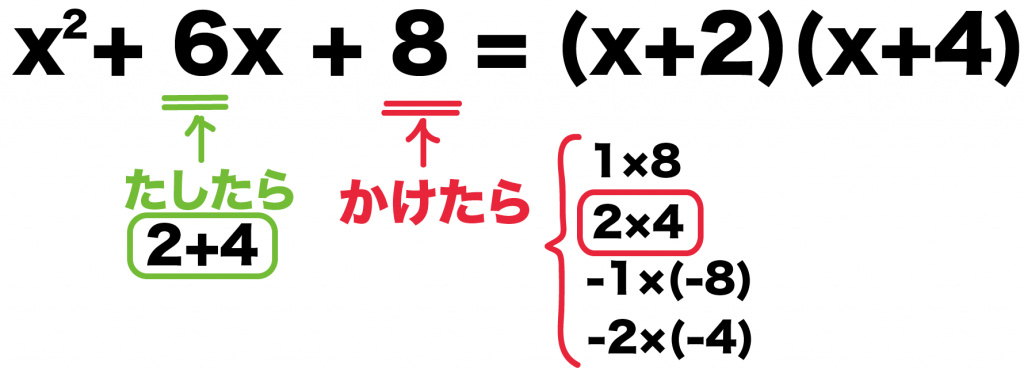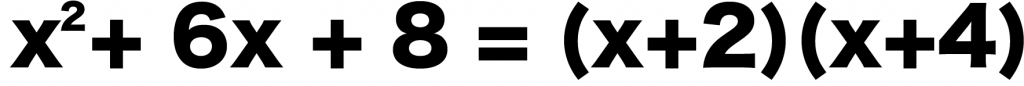【中学数学】因数分解の2つの公式の覚え方

因数分解の公式の覚え方ってあるの？？

こんにちは！この記事をかいてるKenだよ。列がうまれたね。

中学数学でならう因数分解の公式は3つあるよ。

• a² – b² = (a+b)(a-b)
• a² + 2ab +b² = (a+b)²
• x² + (a+b)x + ab = (x+a)(x+b)

また公式おぼえるのかよ。。。。。

って感じだよね。ただ、安心してほしい。

じつはこれ、

展開の公式（乗法公式）を逆にしただけなんだ。

べつに新しいことを学んでるわけじゃない。

見方を逆にしただけさ。

だけど、乗法公式の逆っていわれてもピンとこないし、

因数分解に特化した公式の覚え方を知りたいよね。

そこで今日は、

因数分解の公式の覚え方

をわかりやすく解説してみたよ。

公式をおぼえたいときに参考にしてみて。

因数分解の公式を2種類にわけた覚え方

中学数学でならう因数分解の公式はシンプル。

おおきくわけると2種類しかないんだ。教科書では3つぐらいあるってならうけどね。

それは、

• 2つの項を因数分解する公式
• 3つの項を因数分解する公式

の2つさ。

因数分解したい文字式の項が何個あるのか？？

ってことによって使い分けるんだ。

さっきの公式でいうと、

a² – b² = (a+b)(a-b)

が2つの項専用の因数分解の公式。

ほかの2つの、

• a² + 2ab +b² = (a+b)²
• x² + (a+b)x + ab = (x+a)(x+b)

が3つの項を因数分解するときにつかう公式なんだ。

2種類なら公式を覚えれそうだね！

それぞれ順番にみていこう！

2つの項を因数分解できる公式の覚え方

2つの項を因数分解できる公式は1つしかないよ。

a² – b² = (a+b)(a-b)

この因数分解の公式はなんというか、

分解型の公式

だね。

なぜなら、2乗になっている数字をバラバラにしてあげて、＋と-でくっつけるだけだからね。

2つ重なっているものを1つずつに分解してまとめてあげる。

だから、ぼくは分解型ってよんでるんだ。

とりあえず、焼き肉をイメージしてほしい。

同じ肉が重なっちゃっていて、うまく焼けてないお肉たちをね。

こいつらをおいしく調理するために、いっかいバラバラにしてやる。

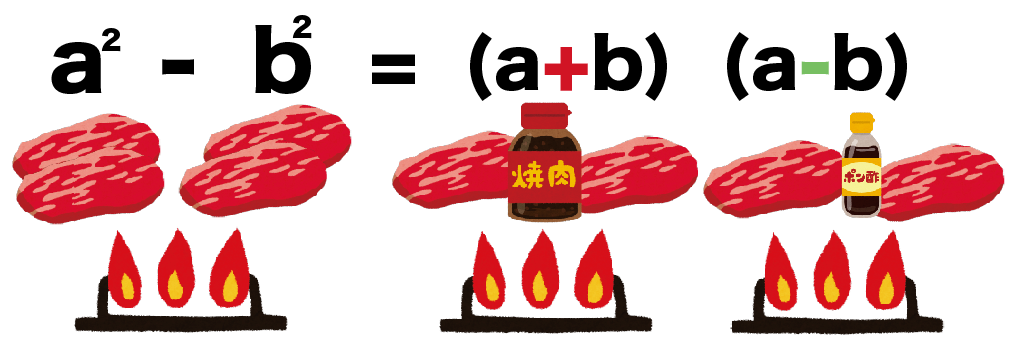
んで、わけたお肉には違うたれ（符号）をつけてやるんだ。

ぜんぶおなじ味じゃ飽きちゃうでしょ？？

焼き肉のたれをかけるやつと、ポン酢かけるやつにわけてみるって感じ。

こんな感じで、

2つの項を因数分解する公式は、

1. 2乗になってるもとの数をばらす
2. ＋と-で結ぶ

っていう2ステップで因数分解できちゃうのさ。

たとえば、

9x² – 4y²

を因数分解してみよう。

これをまずは、

a² – b²

の形になおしてやろう。

• 9x² = (3x)²
• 4y² = (2y)²

だから、

9x² – 4y²
= (3x)² – (2y)²

になるね。

つまり、重なっているお肉は「3x」と「2y」なわけだ。

お肉をバラバラにして、違うソース（符号）でむすんでやると、

9x² – 4y²
= (3x)² – (2y)²
= (3x +2y) (3x -2y)

になるよ。

この公式を使うときは、

「○○の2乗」になるように分解してみよう！

3つの項を因数分解できる公式の覚え方

因数分解の公式で「3つの項」を因数分解できるのは、

• a² + 2ab +b² = (a+b)²
• x² + (a+b)x + ab = (x+a)(x+b)

の2つだね。

だけど、実際は最後の、

x² + (a+b)x + ab = (x+a)(x+b)

さえ覚えてれば大丈夫。

3つめの公式の「b」に「a」を代入すると2つめの公式になるからね。

2つ目の「a² + 2ab + b²」は覚えなくても痛くもない。ちょっとカユいけどね。

ぼくは個人的に、この因数分解の公式を、

パズル型の公式

とよんでいるよ。なぜなら、

かけたら右、たしたら真ん中になる2つの数・文字を推理するからね。

まるで、クロスワードパズルみたいでしょ？

たとえば、

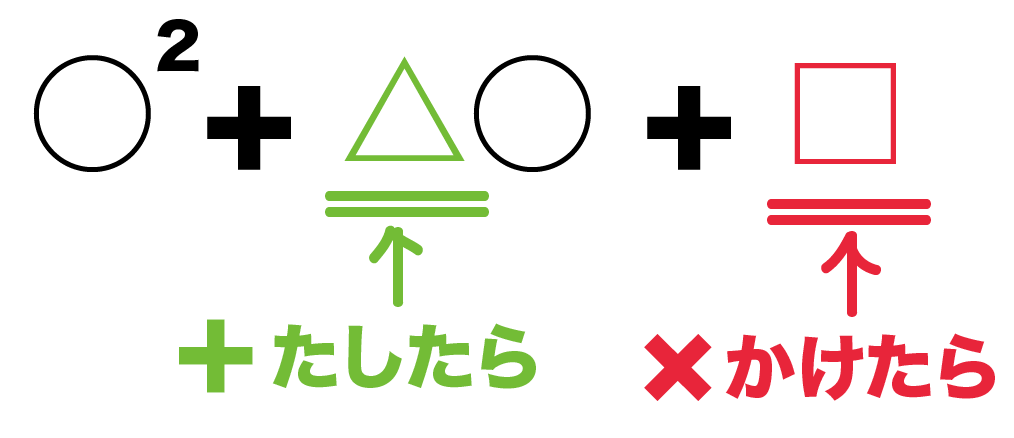
○² + △○ + □

っていう式があったとしよう。

このとき、

• かけたら⇒ □
• たしたら⇒ △

になる2つの数字・文字の組み合わせを考えればいいんだ。

まずは、「かけたら□になる組み合わせ」を考えてみよう。

もし、a・bっていう2つの文字が、

• ab = □
• a+b = △

になるとしたら、

○² + △○ + □ = (x+a)(x+b)

になるんだ。

つまり、3つの項を因数分解する公式では、

• かけたら□になる
• たしたら△になる

2つの数字・文字の組み合わせを推理すればいいんだ。

たとえば、

x² + 6x + 8

をイメージしてみて。

3つの項でできているから、

x² + (a+b)x + ab = (x+a)(x+b)

のパズル型の公式をつかうよ。

• かけたら⇒8
• たしたら⇒6

になる組み合わせを推理していこう。

まず、「かけたら8になる数」を考えてみる。

かけたら8になる数の組み合わせは、

• 1×8
• (-1)×(-8)
• 2×4
• (-2)×(-4)

の4通りだね。

この4通りの組み合わせのうち、たしたら6になるのは、

• 2
• 4

のペアーだ。

これが因数分解の公式のaとbにあたるってことさ。

だから、公式で因数分解してやると、

x² + 6x + 8 = (x+2)(x+4)

になるね。

おめでとう！

項が2つ3つでもどーんとこいだね！！

まとめ：因数分解の公式は項の数によって使い分けろ！

因数分解の公式はたくさんあるように思えるけど、

実際わけてみると2種類。

• 項2つを因数分解できる公式
• 項3つを因数分解できる公式

しかないんだ。

自分が因数分解したい文字式の項は何個あるのか？？

をチェックしてみよう。

そんじゃねー

Ken