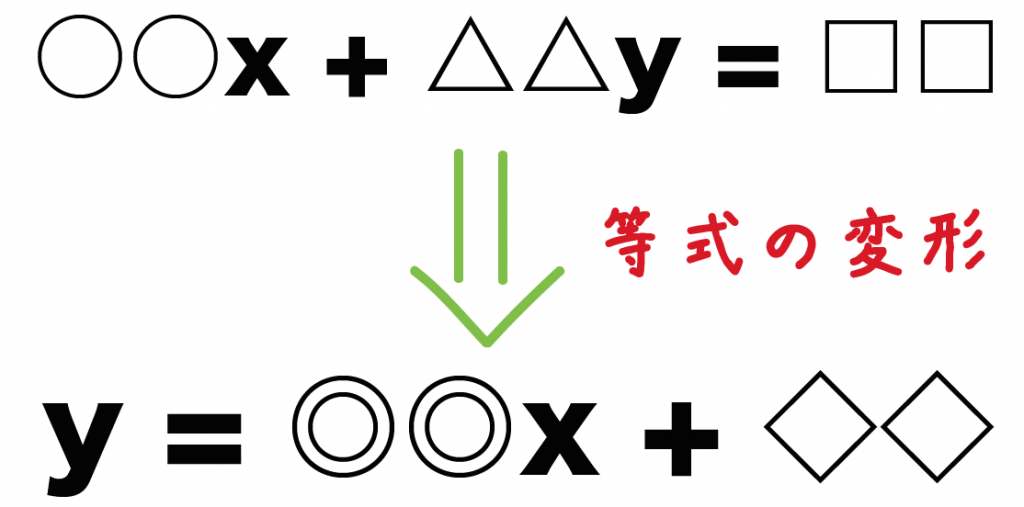方程式を一次関数のグラフにしろ？？
こんにちは！この記事をかいているKenだよ。10円玉たまってるね。
「方程式」を「一次関数のグラフ」にする。
これが案外、むずかしい。
方程式なんか一次関数にみえないもん。
グラフをかくのもめんどくさそうだね。
そこで今日は、
「二元一次方程式」を「1次関数のグラフ」にする方法を2つ紹介するね。
よかったら参考にしてみて。
二元一次方程式をグラフにする2つの書き方
二元一次方程式って、
文字が2つある1次方程式
のことだよね。
この二元一次方程式をグラフにしてよ？
みたいな問題がちょくちょくでてくるんだ。
たとえば、つぎのような例題みたいにね↓↓
（1）3x + y = 7
（2）2x + 3y = 6
つぎの2つの書き方で攻略していこう！
かき方1. 「 yについて等式を変形する方法」
1つ目の書き方は、
yについて等式を変形しちゃう方法だ。
等式の変形をつかって、
○○x + △y = ××
を、
y = ○○x + ××
に変形してやればいいのさ。
これは一次関数のカタチと一緒だね。
だから、一次関数のグラフの書き方をつかえばいいんだ。
この書き方は、
yの係数が「1」のときに使うのが便利だよ。
だって、xを移項するだけでいいからね。
例題でいうと、（1）の二元一次方程式だね。
3x + y = 7
をyについてといてやると、
y = -3x + 7
になる。
こいつは、傾き「3」、切片「7」の一次関数と同じ。
あとは一次関数のグラフの書き方通りにかくと、
こうなるね↓↓
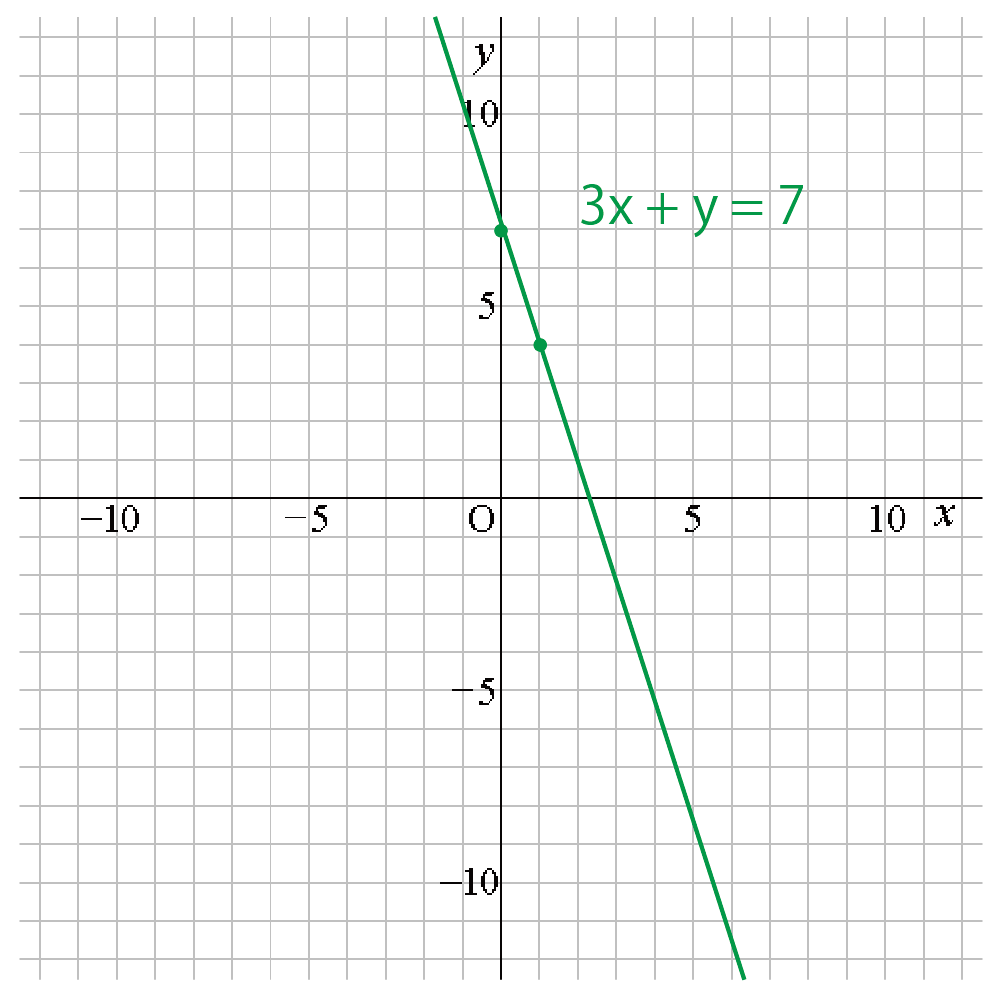
等式の変形ができればこっちのもんさ！
かき方2. 「x軸とy軸の交点を求める方法」
x・y軸との交点を求める方法だ。
方程式に、
- x = 0
- y = 0
を代入して、x・y軸との交点をさがせばいいんだ。
この書き方は、
yの係数が1より大きいときに便利だよ。
たとえば、例題の（2）の一次関数だね。
（2）2x + 3y = 6
x・y軸との交点をさがすために、
- x = 0
- y = 0
をそれぞれ代入してみよう。
x = 0のとき、
3y = 6
y = 2
になる。つまり、y軸との交点は（0, 2）ってわけさ。
また、y = 0のときは、
2x = 6
x = 3
になる。つまり、x軸との交点は（3, 0）ってわけだね。
2つの交点をむすぶとグラフがかけるよ。
こんな感じでね ↓↓
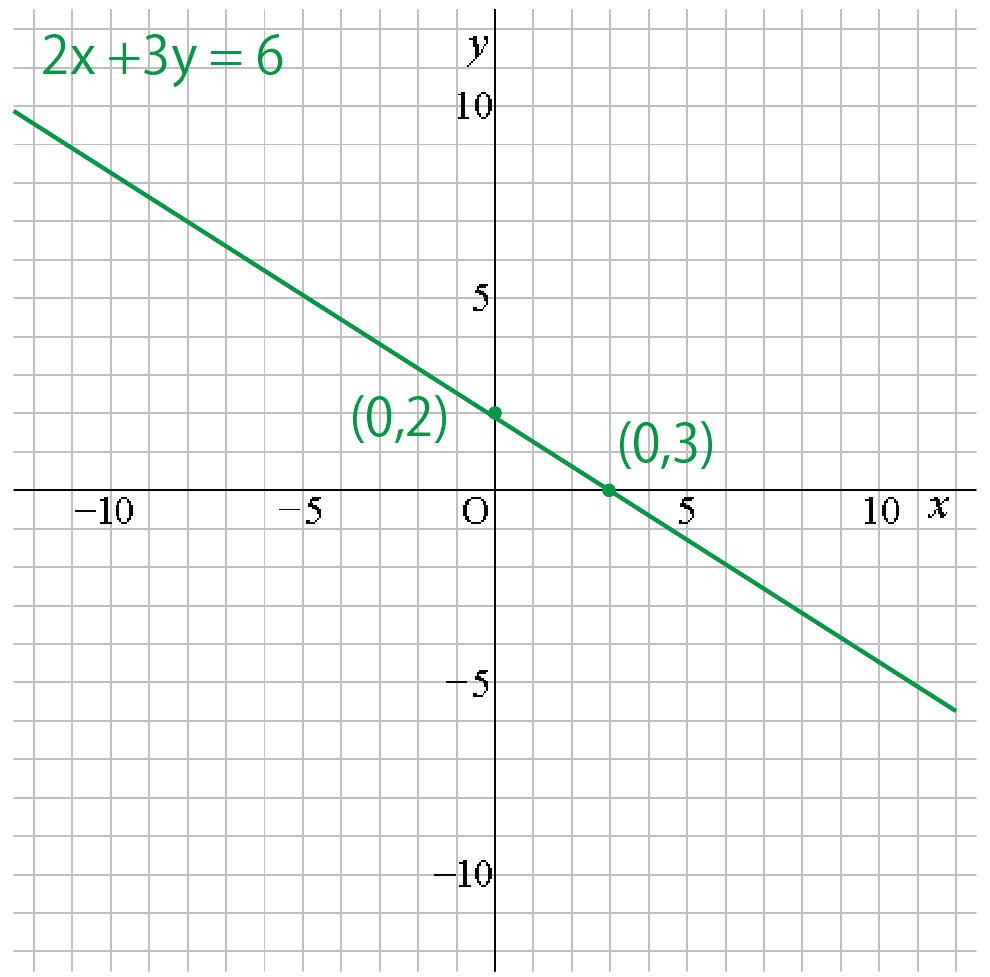
まとめ：yの係数によって書き方を使い分けよう！
コツは、
yの係数によって書き方をかえる
ことだ。
- yの係数が1 → yについて変形してから解く
- yの係数が1より大きい → x・y軸との交点を求める
たまにでてくる問題だからマスターしておこうね。
そんじゃねー
Ken
