ひし形の対角線は垂直に交わるってホント？？
こんにちは！この記事をかいているKenだよ。明太子が恋しいぜ。
ひし形の対角線にはつぎの性質がある。
それは、
対角線は垂直に交わる
ってやつだ。
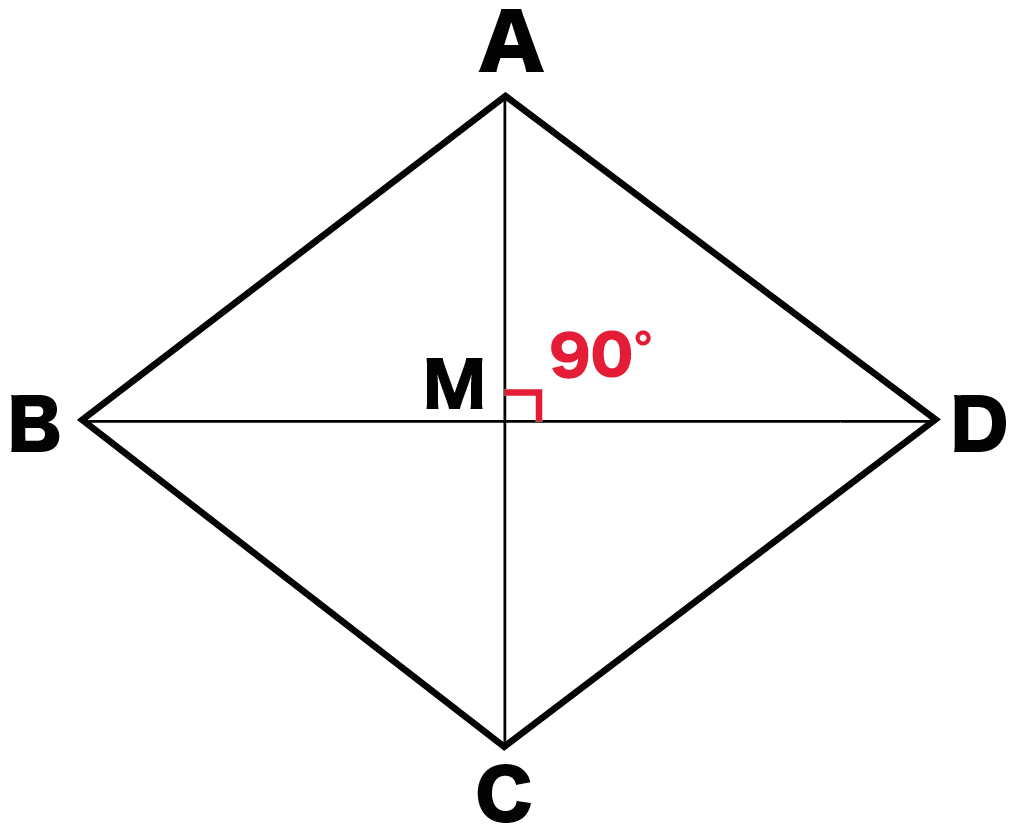
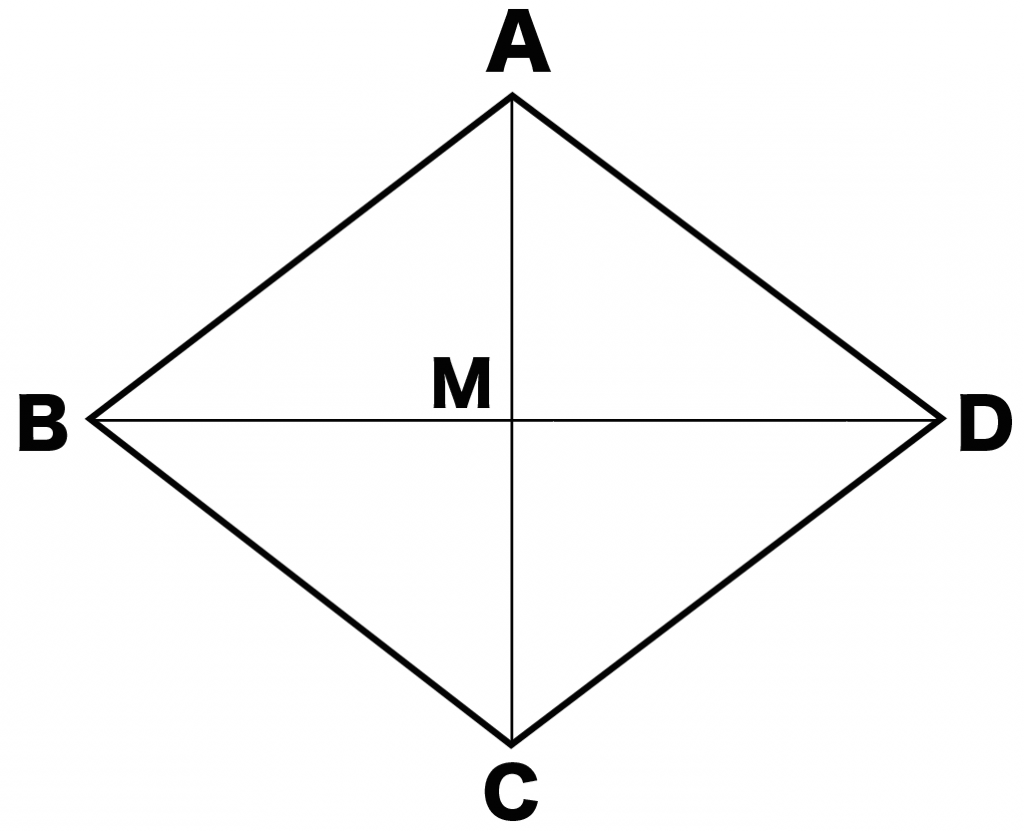
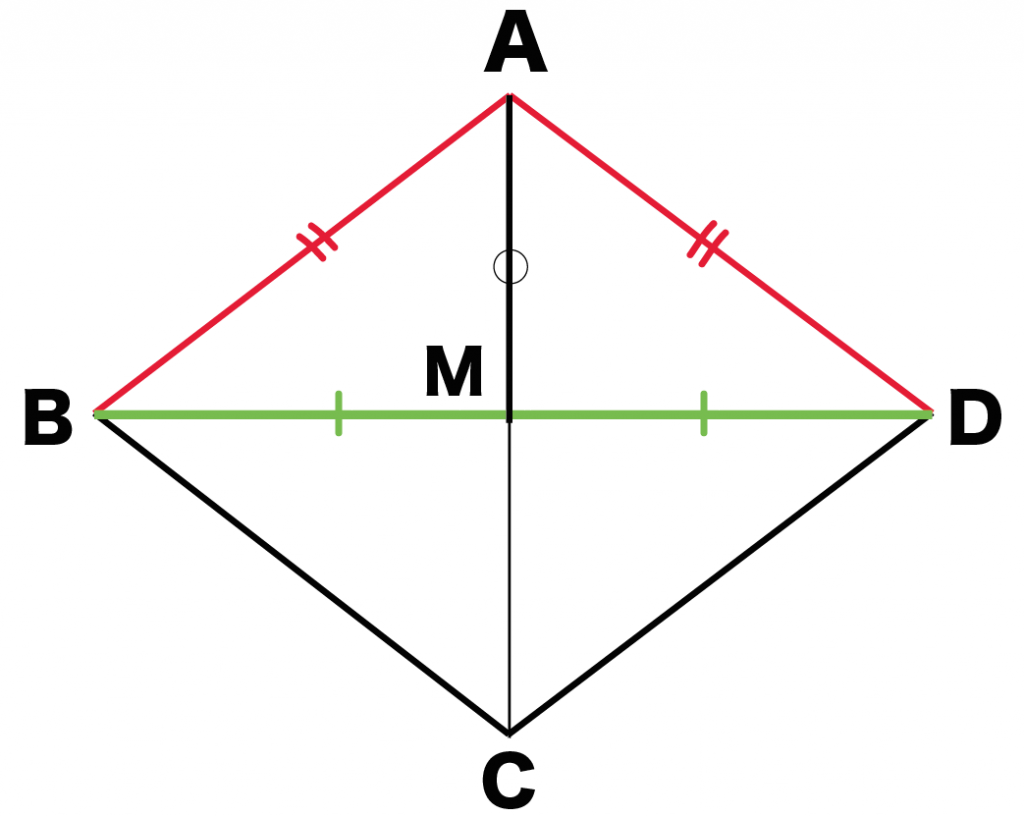
たとえば、ひし形ABCDがあったとしよう。
対角線の交点をMとすると、
AC⊥BD
になるんだ。
つまり、
角AMD = 90°になるってわけ。
むちゃ便利そうな性質だね。
だけど、
なぜ、ひし形の対角線は垂直に交わるんだろう？？
ちょっと不思議すぎるよね。
そこで今日は、この謎を証明していくよ。
よかったら参考にしてみて。
なぜ、ひし形の対角線が垂直に交わるの？？
さっそく証明していこう。
つぎの4ステップで証明できちゃうんだ。
例の「ひし形ABCD」をつかって証明していこう。
証明の方向性としては、
△ABMと△ADMの合同を証明していくよ。
Step1. ひし形の定義をつかう
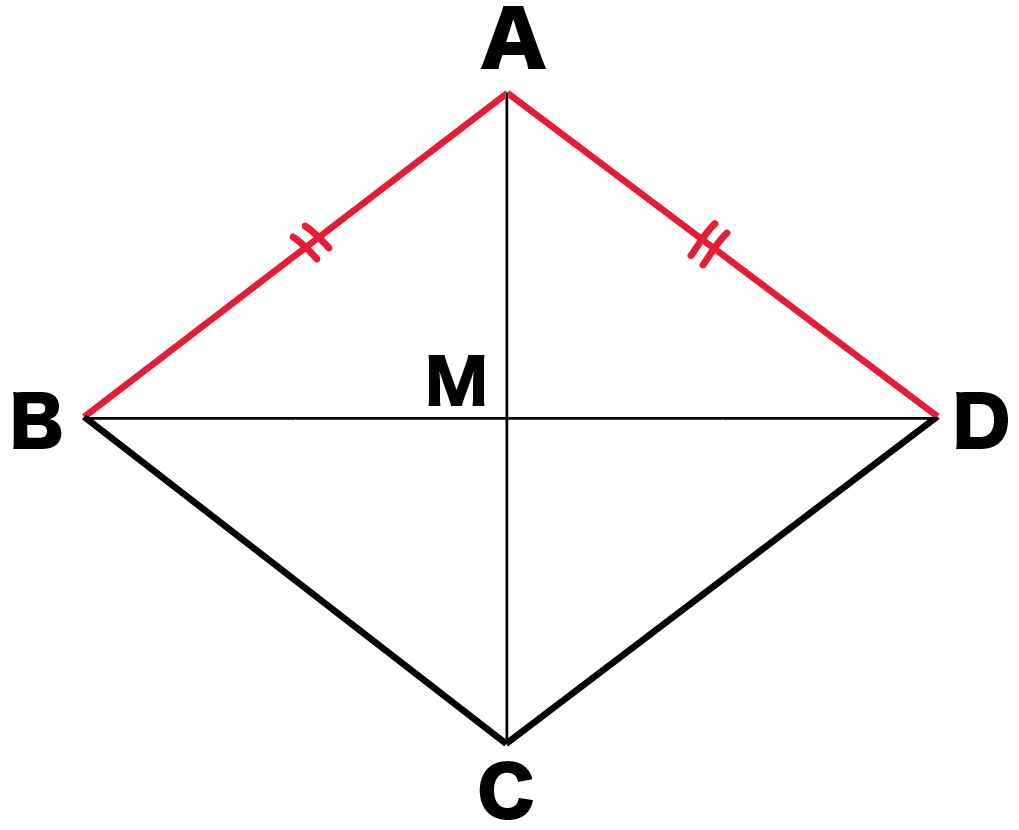
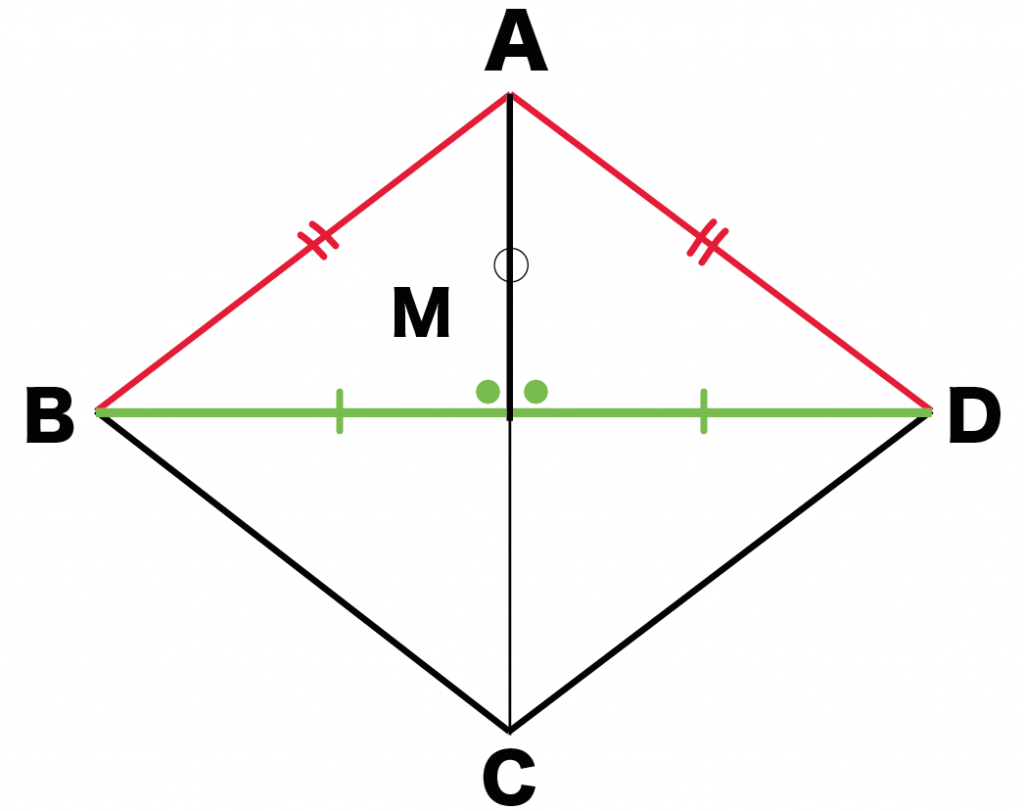
△ABMと△ADMにおいて、
ひし形の定義（4つの辺がすべて等しい）より、
AB = AD・・・(1)
Step2. 平行四辺形の性質をつかう
ひし形は平行四辺形だから、
平行四辺形の性質がつかえるね。
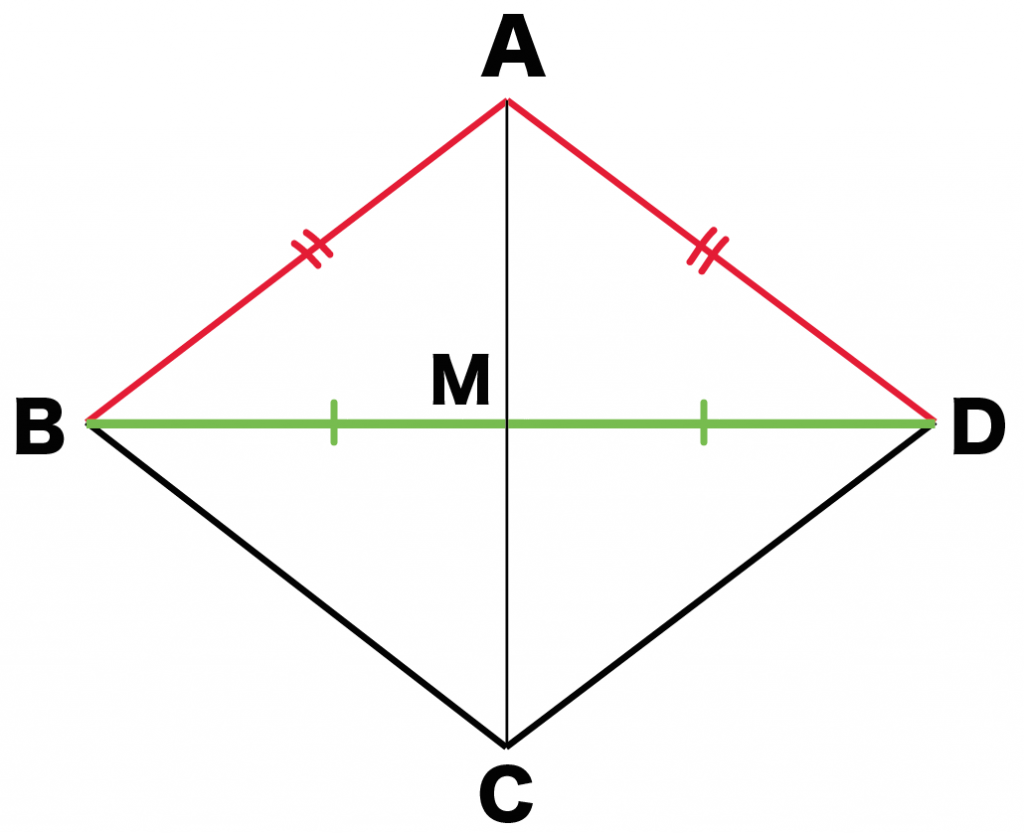
対角線は中点でそれぞれ交わる
という性質より、
BM = DM・・・(2)
Step3. 三角形の合同条件をつかう
AMは共通だから、
AM = AM・・・(3)
(1)・(2)・(3)より、
3つの辺がそれぞれ等しいから、
△ABM ≡ △ADM
がいえるね。
Step4. 合同な図形の性質をつかう
合同な図形同士の対応する角はそれぞれ等しいから、
角AMB = 角AMD・・・(4)
になるね。
角AMBと角AMDをたしたら直線になっているから、
角AMB + 角AMD = 180°・・・(5)
になるはず。
(4)、(5)より、
角AMD + 角AMD = 180°
角AMD = 90°
になるね。
よって、
ひし形ABCDの対角線は垂直に交わることになるよ。
まとめ：ひし形の対角線は垂直に交わる！
ひし形の性質でおさえておきたいのは、
対角線が垂直に交わる
ということ。
性質をただ暗記するだけじゃなくて、
なぜ対角線が垂直に交わるのか？？
ということもおさえておこう。
そんじゃねー
Ken
