
恒星の等級とはズバリ、
星の明るさを表すための「明るさの単位」
だ。
星がどれくらい明るく見えるかを数値で表してるんだな。
観測や比較のために使われているぞ。
で、恒星の明るさは1等級や2等級といった等級で表される。
それぞれの明るさの恒星は1等星、2等星と呼ばれるんだ。
等級の数が小さいほど、星が明るい!

たとえば、高価な物ほど値段が高いって思うだろう?
でも星の明るさは逆なんだ!
明るい星は小さい数字で表されて、本当に明るい星はさらになんと0等級や-1等級で表されることもあるんだぜ!
等級の具体例を見ていこう。
太陽の明るさはなんと
-27等級!!
満月は、
-13等級
になるんだぞ!

それに比べて、暗い所だと肉眼で見えるのは6等星までの星なんだ。
星の数についても見てみよう!
全天の恒星の数は1等星から6等星までで、約8600個だ。
この中で、特に明るい1等星は数が限られていて、より特別な存在なんだぞ。
人工の光が少なく、空が十分に暗い場合に、6等星までの恒星が見られるんだ。
街の明るいライトがないところなら、たくさんの星を肉眼でも楽しめるんだぜ!
次の表は具体的な星たちのデータさ。最後にチェックしておこうな。
| 星の名前 | 等級 | 等星(分類) |
|---|---|---|
| 太陽 | −26.74 | 等外(圧倒的に明るい) |
| 月(満月) | −12.6 | 等外(非常に明るい) |
| シリウス | −1.46 | 0等星クラス(1等星より明るい) |
| ベテルギウス | 0.50 | 1等星 |
| ポラリス(北極星) | 1.98 | 2等星 |
| ミモザ(おおかみ座β星) | 3.0 | 3等星 |
| みなみのうお座 θ星 | 4.0 | 4等星 |
| カシオペヤ座 ρ星 | 5.0 | 5等星 |
| しし座 54番星(54 Leonis) | 6.32 | 6等星(肉眼の限界) |


宇宙の距離感はハンパないぞ!
そこで使われるのが天文単位と光年だ。
天文単位は、太陽と地球の距離を基準にした単位だ。
つまり、太陽と地球の距離を1天文単位ってことにしたんだな。

これはなんと、
約1億5,000万キロメートル!!
おいらたちが普段使ってるメートルやキロメートルとはケタが違う大きさだ。
この天文単位を使えば、地球と他の惑星の距離を表しやすくなるんだぞ。
光年は、光が1年間に進む距離だ。

光の速さは毎秒約30万キロメートルだから、1年でどこまで行けるか考えてみろ!
その距離が約9兆5,000億キロメートル。
正確に計算すると、
$$1\ \text{光年}
= 30\,0000\ \text{km/s} \times (60 \times 60 \times 24 \times 365)\ \text{s}$$
$$\approx 9.46 \times 10^{12}\ \text{km}$$
だ。
デカすぎて想像できないかもしれないけど、遠い恒星や銀河までの距離を表すのに便利なんだ。
よし、それじゃあ天文単位と光年を実際に使ってみようか。
太陽からの距離を天文単位で並べるとこんな感じだ。
| 惑星名 | 太陽からの距離(天文単位) |
|---|---|
| 水星 | 約 0.39 天文単位 |
| 金星 | 約 0.72 天文単位 |
| 地球 | 1 天文単位(基準) |
| 火星 | 約 1.52 天文単位 |
| 木星 | 約 5.20 天文単位 |
| 土星 | 約 9.58 天文単位 |
| 天王星 | 約 19.2 天文単位 |
| 海王星 | 約 30.1 天文単位 |
太陽系の惑星は 数十天文単位以内 に全部収まっている。
つまり天文単位は太陽系の“ご近所距離”を測るのに向いているんだ。
ところが、太陽の外に出ると距離が一気にぶっ飛ぶ!
ぶっ飛び過ぎていて、天文単位じゃ物足りないから、光年を使うんだな。
| 天体名 | 距離 |
|---|---|
| プロキシマ・ケンタウリ(太陽系に一番近い恒星) | 約 4.24 光年 |
| アルファ・ケンタウリA/B(近くの恒星系) | 約 4.37 光年 |
| シリウス(おおいぬ座の明るい星) | 約 8.6 光年 |
| ベテルギウス(オリオン座の赤い巨星) | 約 550 光年 |
| 北極星(ポラリス) | 約 433 光年 |
| アンドロメダ銀河(恒星ではなく銀河) | 約 250万光年 |
太陽系に一番近い恒星のプロキシマ・ケンタウリを見てみようか。
kmに直すと、
$$4.24\ \text{光年}
= 4.24 \times 9.4607 \times 10^{12}\ \text{km}$$
$$\approx 4.01 \times 10^{13}\ \text{km}$$
離れている!
天文単位なら、
$$4.24\ \text{光年}= 4.24 \times 63\,241\ \text{天文単位}$$
$$\approx 2.68 \times 10^{5}\ \text{天文単位}$$
これぐらい。
どうだ?? 宇宙って本当に広いよな?


まず銀河からだな。
銀河とは、
恒星やガス、ちりが集まった巨大な天体の集まり
だ。

宇宙には無数の銀河が存在していて、なんとその数、
約1兆個!
たとえば、
っていう銀河が宇宙にはあるぜ。
そして、その銀河には数億から数千億個の恒星が含まれているぞ。
銀河は形によっていろいろな種類がある。
たとえば、渦巻き型や楕円形、そして不規則な形の銀河なんかがあるぜ。
それぞれの形は銀河の年齢や進化の過程によって決まるんだな。
次に銀河系について話すぞ。
銀河系とは、
地球が属する銀河のこと
だ。

銀河系には約千億個の恒星が含まれていて、その中心をぐるっと回るように地球や太陽が存在しているわけよ。
銀河系は盤状の形をした銀河として知られているぞ。
その中には恒星だけでなく、恒星を作るもとになる気体やちりも混ざっているんだぜ。
銀河と銀河系、その最大の違いは言葉の使われ方にあるぞ。
銀河は一般的にあらゆる星の集まりを意味する。
一方で銀河系は、地球や太陽が属している特定の銀河を指す言葉なんだ。
ここでたとえ話をしてみよう。
銀河というのは、世界中にある「国」のようなもの。
アンドロメダ銀河も、さんかく座銀河も、すべて「国」のように独立して存在している。
その中で銀河系は、例えるなら日本だ。
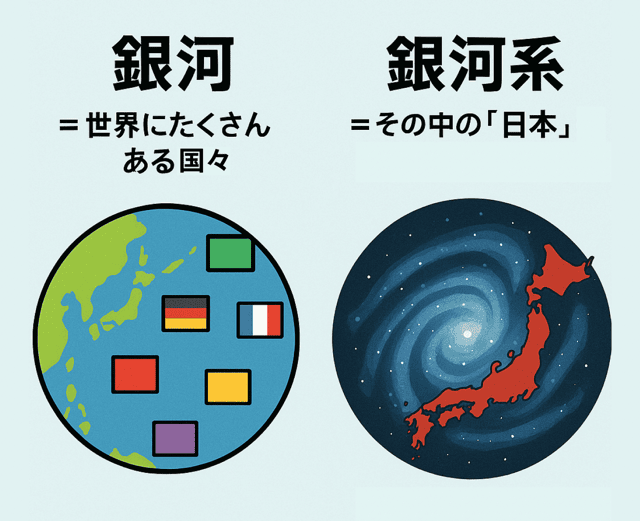
たくさんある世界の国の中の1つに過ぎないわけさ。
つまり、
というイメージだな。
太陽系はその「日本」の中の、さらに「1つの家」にすぎないと考えれば、スケール感がつかみやすいぞ!


銀河系と太陽系はどちらも宇宙にいるけど、それぞれ持っているスケールや特徴が違うんだ。
銀河系は、巨大な星の集団の1つさ。

宇宙の中でも大きな「都市」みたいなもんだ。
直径は10万光年以上で、約1000億個の恒星を抱えている巨大な円盤さ。
恒星だけでなく、ガスや塵もいっぱい含まれていて、星々が誕生する素となる場所でもあるんだ。
太陽系は、その銀河系の中にある無数の恒星系のうちの1つだ。
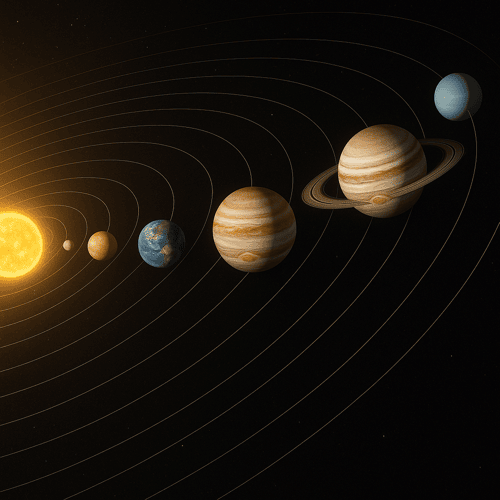
地球がここに所属しているぞ。
中心にでっかい太陽があって、その周りを8つの惑星やその他の小天体がぐるぐるしてる。
まるで家族みたいにみんな太陽の周りに集まって、地球もその一員なんだ。
では、違いを見ていこう!
ズバリ、
規模が違う!
銀河系は巨大な星の集団で宇宙の「大都会」。
一方、太陽系はその中の1つの恒星系。例えるなら、都会の中の1つの町にある1軒の家くらいの大きさだ。

銀河系が東京都なら、太陽系は練馬区の中の 1軒の家くらいっていうスケールの違いなんだな。
だから、太陽系の中に所属する地球はもっと小さい。地球を例えるなら、庭にある小石ぐらいになっちまうかもな。
この違いを理解することが、宇宙の果てしない広がりを感じる一歩になるってことだ。
今回の学びのポイントをまとめておこう。


宇宙を見上げるたびに、たくさんの星がキラキラ輝いて見えるよな。
ここでは宇宙の勉強出てくる重要キーワード、
を解説するぞ。
天体ってのは、宇宙に存在する物体のことだ。
夜に輝く星や月、太陽などが天体に含まれる。
とにかく、空に見えるものは全部天体って感じだな!

恒星は自ら光や熱を放つ天体だ。
星座を形づくるのがこの恒星なんだ。

空がよく見えれば、6等星までの恒星を肉眼で見られる。
等級で明るさが表され、1等級、2等級のように呼ばれるんだ。
惑星は恒星の周りを回る天体で、自らは光を放たない。

太陽系以外にも約2000個の惑星が見つかっているんだ。
ある程度の質量と大きさを持っているのがポイントさ!
違いをまとめよう。
天体は、恒星・惑星が所属するグループの名前だ。
恒星は天体だし、惑星も天体だ。
果物に例えるとわかりやすいな。
りんごも果物だし、バナナも果物だろ??
つまり、グループ名は「果物」で、りんごとバナナはその一種さ。
この事情は恒星と惑星だって同じ。
つまり、天体はグループ名で、恒星と惑星はその一種なんだ。
でも、天体は恒星じゃないし、惑星も恒星じゃない。ここのところはごっちゃにしないようにな!
果物はりんごじゃないだろ? それと同じさ。
オッケー、そいじゃ、天体の中の「恒星」と「惑星」の違いが気になるよな。
それは、
光を発しているかどうか
だ!
これが、大きな違いさ。

ってところがポイントだ。
りんごとバナナ、おいしさの魅力が違うだろ?
それと同じだ。
テスト前に復習しておいてくれよな!


エネルギーの保存とはズバリ、
エネルギーの種類は変わることあれど、その総量は一定
という理科の大基本さ。
例えば、ジェットコースターのことを考えてみよう。

あのスリルの背後には、まさにエネルギーの保存があるのさ。
ちょっと考えてみよう。
ジェットコースターが頂上にあるとき、ポテンシャルエネルギー(位置エネルギー)が最高潮。
下に向かってコロコロ滑ると、エネルギーは運動エネルギーに変わる。
でも、そのとき失うエネルギーもあるんだ!
例えば、摩擦で熱になるエネルギー。そして、風切音として音のエネルギーに変わるものもあるぞ。
手回し発電機もエネルギー変換の良い例なんだ。

手でハンドルをぐりぐり回すと、ハンドルの動き(運動エネルギー)は中で電気エネルギーに変わるんだ。
驚くなかれ。
その電気エネルギーが今度は
に変えられるんだ。
発電した電気エネルギーを好きなエネルギーの形にして利用できるってこったな。
電球をつけたり、オルゴールを鳴らしたりできる。
でも、発電の途中で失われるエネルギーもあるぞ。
例えば、
としてな。手回し発電機グリグリやってると、熱くなってくるし、音もウィンウィン言ってるだろ??
これはグリグリして生み出した運動エネルギーが少し熱や音エネルギーとして失われている証拠さ。
これらの失ったエネルギーの総量を数えると、ハンドルを回して作った運動エネルギーの合計に計算が合っちゃうんだ。
自然の摂理はすごいっちゃ!


この3つの言葉、一度は聞いたことがあるよな!
オラが解説するから、心配しないでくれよ。
どれもこれも、
熱が伝わる現象
の種類のことなんだな。
伝導は、物質が移動せずに熱が伝わる現象だ。
例えば、フライパンを炎であたためるシチュエーションを想像してくれ。
炎の部分から温度の低い周囲へ、どんどん熱が伝わっていくよな??

フライパンは動かないけど、暖まる。これが伝導だ!
次は対流だ!
これは気体や液体が移動することで熱が伝わる現象さ。
例えて言うと、スープを温めるとき、鍋の下の方から熱せられた液体が上昇し、上の冷たい液体が下がって入れ替わる。

給食当番やったやつならわかると思うけど、こうやって鍋全体が温まるんだよな。
つまり、液体やガスが動くことで熱が広がるってわけだ。
最後は放射だ。
光源や熱源から空間をへだてて離れたところまで、熱が伝わる現象さ!
例えば、晴れた天気のいい日を想像しよう。
太陽の光に照らされたところにいると、暖かくなるよな??

太陽からとんでもなく離れているはずなのに、太陽の熱がオラたちに伝わっているわけさ。
これが放射さ!
さあ、ここで伝導、対流、放射の違いをはっきりさせよう。
表でまとめてみたぞ。
| 熱の伝わり方 | どんな仕組み? | 主に起こる場所 | 身近な例 |
|---|---|---|---|
| 伝導 | 物質が動かずに熱が伝わる | 固体 | フライパンの取っ手が熱くなる |
| 対流 | あたたかい液体/気体が上へ、冷たいものが下へ動く | 液体・気体 | 暖房の温風で部屋が温まる |
| 放射 | 空間をへだてて電磁波(赤外線)で熱が伝わる | 真空でも可 | 太陽に当たって体が温まる |
これで、熱の伝わり方を楽しく説明できるようになるはずさ。


仕事率って聞いたことあるか?
こいつは、
どれだけ短い時間にどれだけの仕事をしたか
を表す指標だ。

つまり、同じ仕事でも短い時間でやっちまうと効率がいいわけだ!
10秒で1杯のコーヒーを入れる店員Aさんと、3秒で1杯のコーヒーを入れる副店長Bさんがいたとする。
そう、Bさんの方が短時間で多くの仕事しているよな。
だから、副店長Bさんの仕事率のほうが高いってことさ!
仕事率は次のように表されるんだ。
この式でわかる通り、時間が短ければ短いほど、仕事率は高くなる。
単位はワット(W)だ!
電力の単位と同じだから、電気の勉強と一緒に覚えておくといいぞ。
単位が同じだからって、電力と混ぜないようにな!
たとえば、100J の仕事を 20 秒で行った場合を計算してみよう。
$$ 仕事率 = \frac{100J}{20s} = 5W $$
つまり、
5ワットの仕事率
ってこったな!
次は、100J の仕事を 5 秒で行った場合を考えてみるぞ。
すると、今度は20ワットの仕事率!
つまり、同じ仕事でも素早くやると、仕事率は大きくなる、ってことよ。
学んだことをまとめるぞ!
仕事率は、1秒あたりにやる仕事量で決まる!
公式は $$ 仕事率 (W) = \frac{仕事 (J)}{時間 (s)} $$ で求められる!
ワット(W)は電力と同じ単位だけど、内容は異なるので注意する!


「仕事の原理」とは、一体何のことだと思う?
「仕事の原理」とはズバリ、
どんな道具を使っても、物体を持ち上げたりするときの仕事の大きさは変わらない
っていう考え方なんだ!
たとえば、「てこ(レバー)」を使う場合を考えてみよう。
重たい石をそのまま持ち上げるのは大変だけど、棒と支点を使えば軽い力で持ち上げられるよな。
でも、そのかわりに棒の端を大きく動かさなきゃいけない。
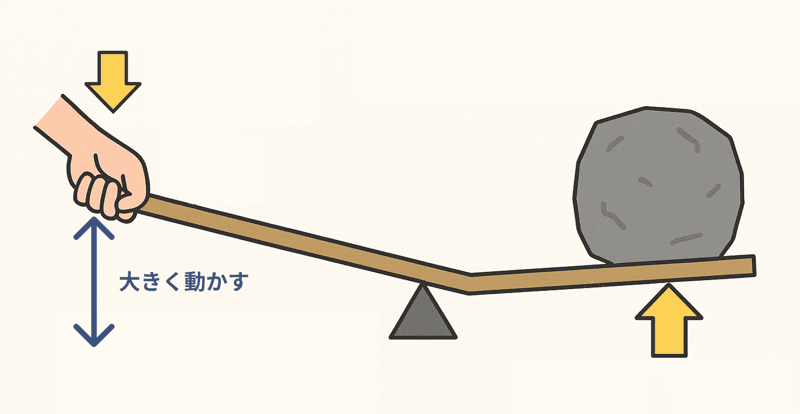
つまり、
ってわけさ。
このように、力と距離のバランスを変えても、全体の「仕事の大きさ」は同じというのが「仕事の原理」なんだ!
この考え方、「仕事の原理」はいろんなところで使われているぞ!
例えば、ドアノブやドライバーみたいな身の回りの道具にも応用されているんだ。
ドアノブやドライバーがこのような仕組みになっているのには、ちゃんとした理由があるんだ。
どちらも「小さい力で大きな仕事をする」ために、力を加える距離を長くとっているんだよ。
ドアノブは円の形をしているよね。
手でノブを回すとき、実は「円の半径の長さ」ぶんだけ力を加える距離が長くなっているんだ。
つまり、ノブの半径が大きいほど、同じ力でもドアの内部機構をより強く回せる。
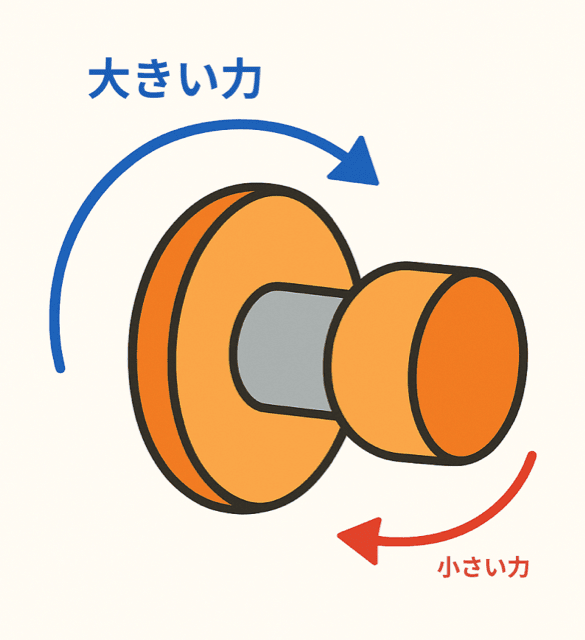
これが「回転のてこ」のような働きをしているんだ。
つまり、半径を大きくして、必要な力を小さくしているぞ!
ドライバーも同じ考え方だ。
持ち手の部分(グリップ)は太くなっているよね?
それは、太いほど回す半径が大きくなり、同じ力でもネジを強く締められるからなんだ。
グリップを太くして、少ない力でネジを回せるようにしているな。
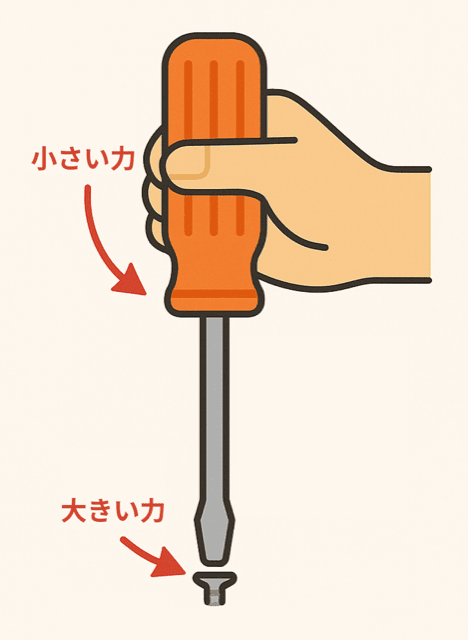
つまり、どちらの道具も「仕事の原理」をうまく利用して、
力を小さく、距離を大きく
というバランスで作業を楽にしているわけさ!


まずは仕事が何かを知っておこう。
物体に力を加えて、その力の向きに移動させたとき、その力が物体に対して「仕事をした」といわれるんだ。
仕事の大きさはズバリ、
の掛け算で表されるぞ。
ってことで、これが仕事の計算公式だ ↓
$$ 仕事 (J) = 力 (N) \times 距離 (m) $$
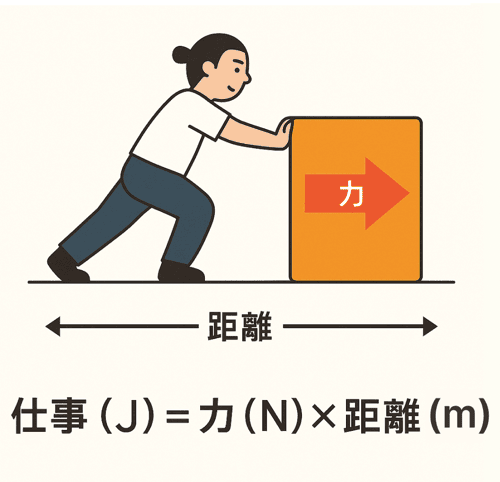
J(ジュール)は仕事の単位さ。
N(ニュートン)は力の単位、m(メートル)は距離の単位だぞ。
たとえば、木箱を 50N の力で 2m 押したシチュエーションを想像しよう。
その場合、
$$仕事 = 50 × 2$$
$$= 100[J]$$
になる。
つまり、50Nの力で木箱を2m押すのに 100ジュール の仕事をした!ってこったな。


力学的エネルギーとはズバリ、
運動エネルギー と 位置エネルギー をまとめた “合計エネルギー” のこと
だ。数式で表すと、
力学的エネルギー = 運動エネルギー + 位置エネルギー
だな。
ちょっと復習すると、
のことだったな。
忘れちまったら運動エネルギーと位置エネルギーの違いで復習しておいてな。
オッケー。力学的エネルギーの正体はわかった。
でも、なんでわざわざ力学的エネルギーって名前をつけてまで勉強するんだな??
それはな、
力学的エネルギーの保存の法則
ってやつがあるからなんだ。
この法則はズバリ、
力学的エネルギー(位置エネルギー+運動エネルギー)は常に一定に保たれる
って法則さ。
ジェットコースターを使って、この法則を見てみよう!
高いところからスタートするジェットコースター。
最初は、高い所にいるから位置エネルギーは大きい。
そして、動き始めると段々速くなっていく。そうなると、運動エネルギーが大きくなるんだ。
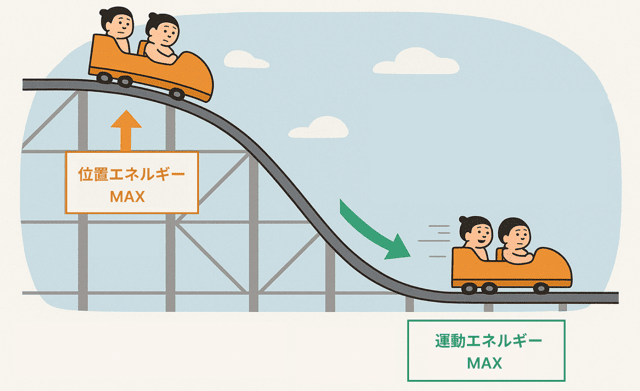
つまり、位置エネルギーが減ったぶん、運動エネルギーが増えるからプラスマイナスゼロってこっちゃ。
不思議なことに、位置エネルギーと運動エネルギーの和はいつも一定なんだ!
具体的にいうとこうだ。
このように、力学的エネルギーの保存の法則は、物体が持つエネルギーが一定であることを示すんだ。
ジェットコースターをみると、エネルギーがうまく変わっていく様子がわかるな。
次回何かを見て運動やエネルギーについて考えるときは、この法則を思い出してみてくれ!


理科の授業でつまずいたキミも、コレを読めばバッチリだ!
運動エネルギーと位置エネルギーって、みんなも聞いたことあるよな?
両方とも前回勉強したエネルギーの一種さ。
同じエネルギーなんだけど、エネルギーを持っている物体の状態が違うぞ。
運動エネルギーは、読んで字のごとく、動いている物体がもっているエネルギー。
位置エネルギーは、高いところにある物体がもっているエネルギーさ。
おっしゃ、まずは運動エネルギーだ。
このエネルギーは、
物体の「速さ」と「質量」によって決まる
んだ。

速ければ速いほど、そして重ければ重いほど、その物体のもつ運動エネルギーは大きくなる。
つまり、お相撲さんが新幹線ぐらいのスピードで動いたら最強ってことだ。
「質量(重さ)」と「速さ」がタッグを組んだとき、運動エネルギーは一気に爆発的に大きくなる。
この運動エネルギーがゆえ、運動している物体は、他の物体を動かしたり、形を変えたりすることで、そのエネルギーを伝えられる。
次は位置エネルギーだ。
高いところにある物体は、地面に落ちる力、つまり重力によってエネルギーをもってるんだ。
そのエネルギーは、
物体の「高さ」と「質量」で決まる
ぞ。
物体が高ければ高いほど、重ければ重いほど、高い位置エネルギーをもつってわけさ!
たとえば、エベレストの頂上にいるお相撲さんなんかは、ものすごい位置エネルギーをもってるってことだ。

