こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。
球の体積の求め方には公式があるんだ。
球の半径をrとすると、体積の求め方は、
$$\frac{4}{3}πr^3$$
になるよ。
つまり、
3分の4 × 円周率 × 半径 × 半径 × 半径
ってことだね。
この公式でどんなボールの体積も計算できちゃうんだ。
たとえば、半径30 [cm]のサッカーボールがあったとしよう。

こいつの体積は「4/3 × π × 半径の三乗」という公式をつかってやると、
$$\frac{4}{3} × π × 30 × 30 × 30= 36000π [cm³]$$
になるね。
これってサッカーボールの中にどれぐらい空気が入っているか?ってことなんだ。
ちょっとすごくない。?
ただ、この公式にも一つだけ欠点がある。
それは、
むちゃくちゃ暗記がむずかしい
ってことさ。
3分の4なんてどっから来た数字かわからないし、半径を何回かけたらいいのかわからない。
これじゃあ球の体積の問題をだされたらやばすぎる・・・・
そこで、今日は、
中学生でもおぼえられる「球の体積の求め方」を解説していくよ。
球の体積の公式を忘れちゃったときに参考にしてみて。
「球の体積の公式」を暗記する方法を伝授しよう。
3分の4 × 円周率 × 半径の三乗
という公式はつぎの語呂を使えばおぼえられちゃうよ。
さんしろう、おいしいパイを持ってある日参上

えっ。
あ、大事だからもう一度繰り返すよ。
さんしろう、おいしいパイを持ってある日参上
なぜこの語呂で「球の体積の公式」おぼえられるのか。
それは、
さんし(3分の4)ろう、美味しいパイ(π)を持ってある(r)日参上(三乗)
になるからさ。
つまり、
という感じで、それぞれの言葉が対応してるってわけ。
だから、
さんしろう、美味しいパイを持ってある日参上

という語呂を覚えてしまえば「球の体積の求め方」の公式も一生忘れないってことさ。
おめでとう!!
中学数学では「球の体積の公式」が使える理由がわからない。
完全に理解するためには「積分」という知識を使わなきゃいけないんだ。
だからこそ、中学生の間は、
さんしろう、美味しいパイを持ってある日参上

という語呂で「球の体積の公式(3分の4 × 円周率 × 半径の三乗)」をおぼえてしまおう。
テスト前にがんばって暗記してみてね。
そんじゃねー
Ken
なぜ球の公式がつかえるのか気になったらみてみて↓
こんにちは!この記事をかいているKenだよ。ライチティーうまいね。
正四角錐の側面積の求め方にも公式があるんだ。
底面の1辺の長さをa、側面の三角形の高さをbとすると、
2ab
で側面積を求めることができるよ。
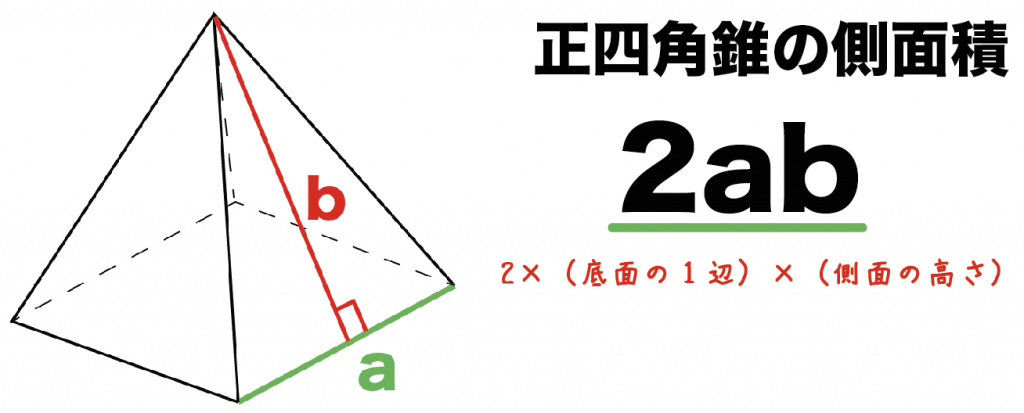
つまり、
「正方形の1辺」×「側面の三角形の高さ」× 2
を計算すればいいってことだね。
今日はこの公式を使えるようにするために例題をといていこう!
つぎの例題をみてくれ↓↓
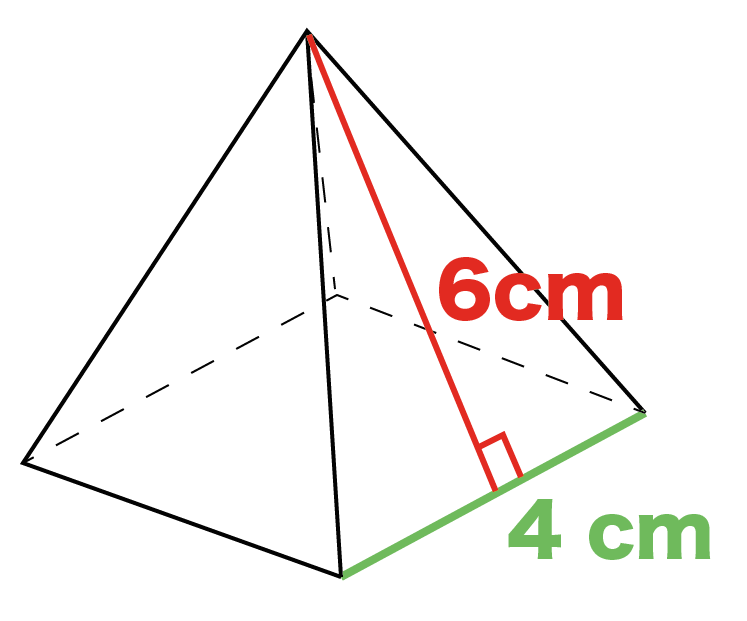
例題
底面の正方形の長さが「4cm」、側面の三角形の高さを「6 cm」の正四角錐の側面積を求めなさい。
この手の問題は2ステップでとけちゃうよ。
1つの側面の面積を計算してみよう。
正四角錐の側面は「三角形」だから、
底面×高さ×1/2
で求めることができるね。

例題の側面の三角形の底辺は「4 cm」、高さは「6 cm」 だったはず。
こいつの面積を公式通りに計算してやると、
4×6×1/2
= 12 [cm^2]
になるね!
ステップ1で求めた「1つの側面積」を4倍するよ!
えっ。なんで4倍なのかって??
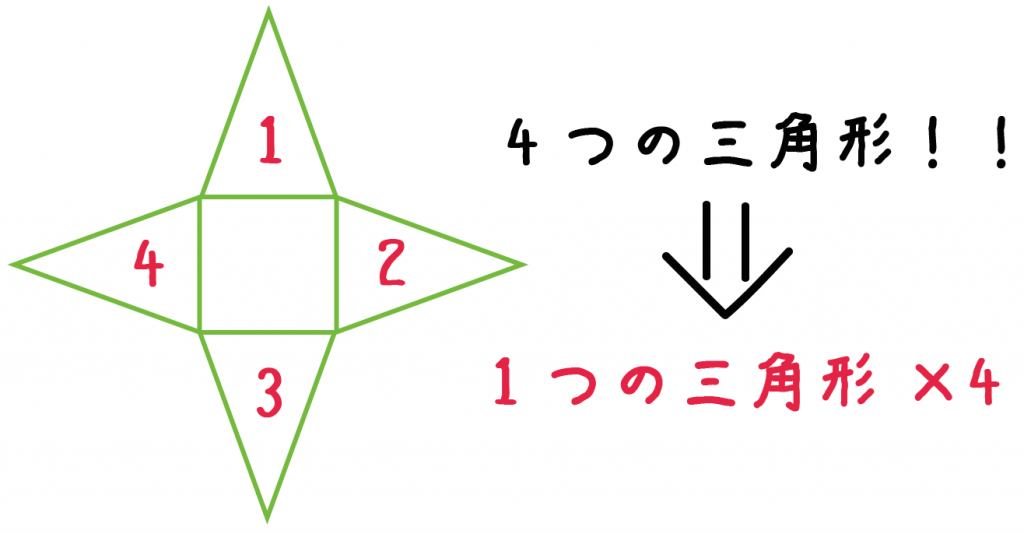
それは正四角錐の展開図をみるとわかるよ。
展開図をかいてみると、
同じ三角形が4つあることに気づくでしょ??
ってことは、1つの側面の面積を4倍してやれば正四角錐の側面積になるわけ!
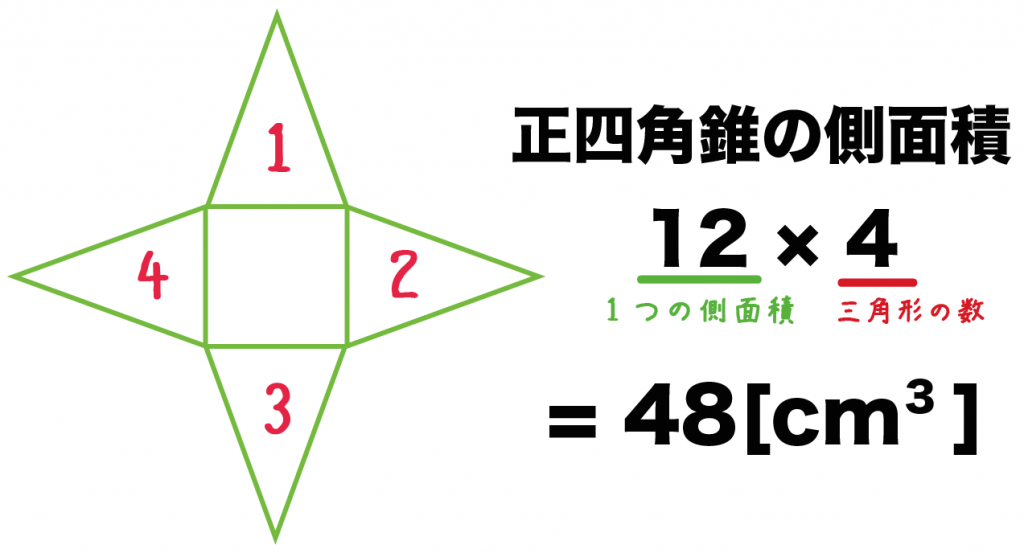
例題の1つの側面積は「12 cm^2」だったよね??
ってことは、こいつを4倍した値が正四角錐の側面積ってことだ。
12×4
= 48[m^3]
になるね。
おめでとう!これで正四角錐の側面積を計算できちゃったね!。
正四角錐の側面積の求め方はどうだった??
公式をつかったら一瞬で計算できちゃう。
だって、
「底面の1辺」と「側面の三角形の高さ」をかけて2倍すればいいんだからね。
公式を使わなくても、正四角錐の展開図をイメージできれば答えらるよ!
テストではミスをしないように気をつけてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。コーヒーは無糖に限るね。
直方体の体積の求め方には公式があるんだ。
直方体のタテの長さをa、ヨコの長さをb、高さをcとしよう。
このとき直方体の体積は、
abc
で計算できちゃうんだ。
つまり、
タテ×ヨコ×高さ
ってことだね。
今日は公式をマスターするために、例題を一緒にといてみよう!
つぎの例題をといてくよ↓↓
例題
ヨコの長さ3cm、タテの長さ6cm、高さを8cmの直方体の体積を求めなさい!
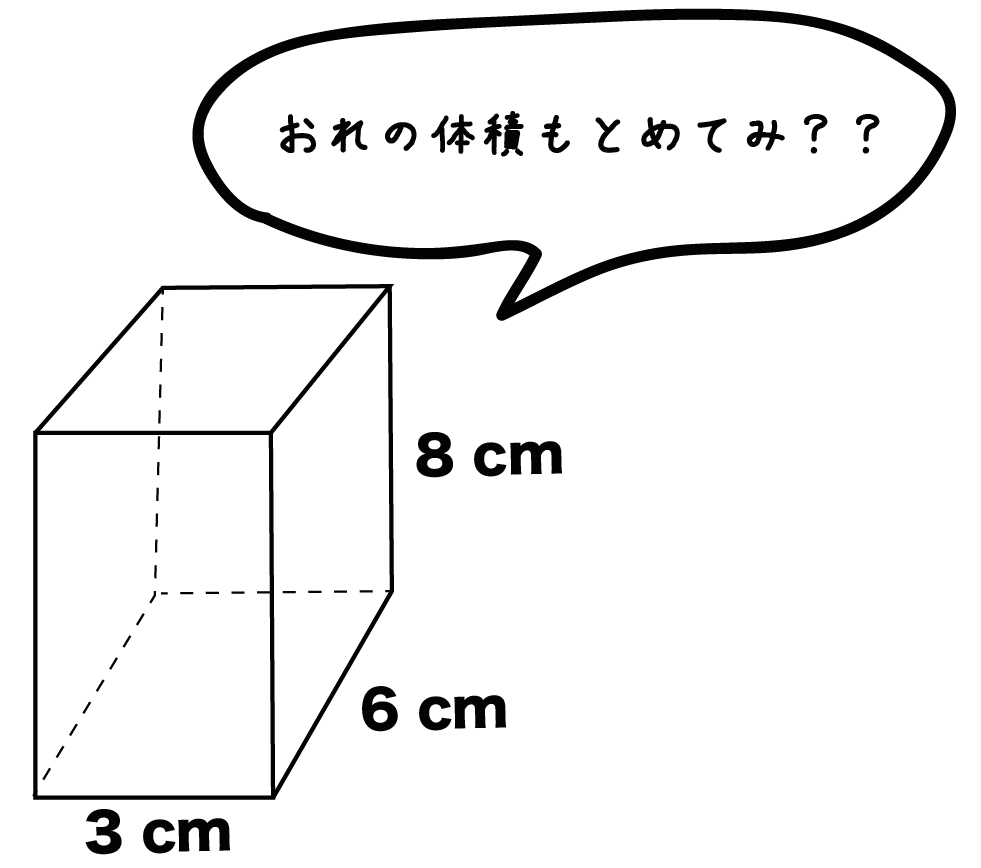
まずは直方体の「ヨコ」と「タテ」の長さをかけてみよう。
「ヨコ」と「タテ」をかけると直方体の底面積が計算できちゃうんだ。

例題でいうと、
タテの長さは「6cm」、ヨコの長さは「3cm」だったね。
こいつらを掛け合わせてやると、
6×3
= 18
になる。
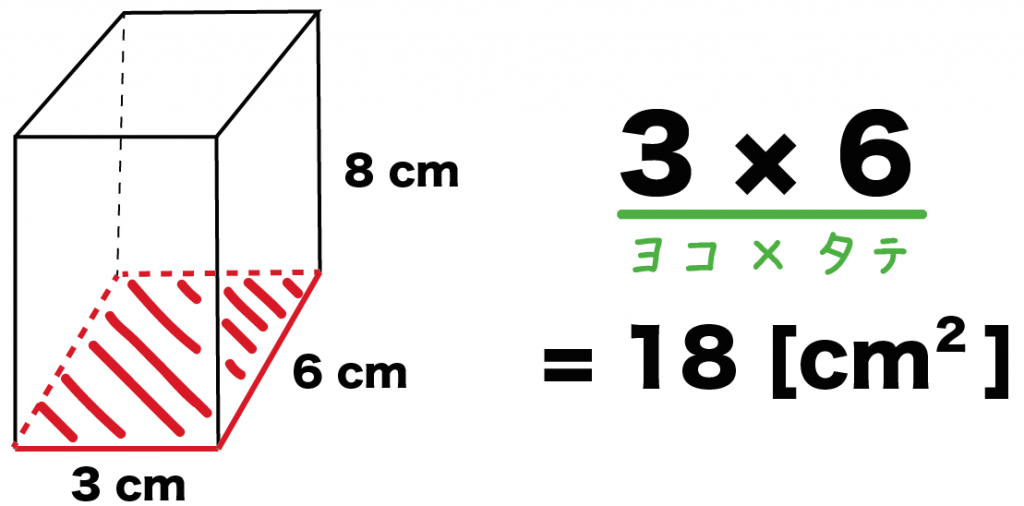
これで直方体の底面積を求めることができたってことさ!
最後に直方体の「高さ」をかけてあげよう。
さっきは直方体の底面積を計算していたよね。これに高さをかけると、直方体の体積になるんだ。

例題の直方体の高さは「8 cm」だったよね??
こいつを「タテ×ヨコ」にかけてやると、
3×6×8
= 144[cm^3]
になるよ。
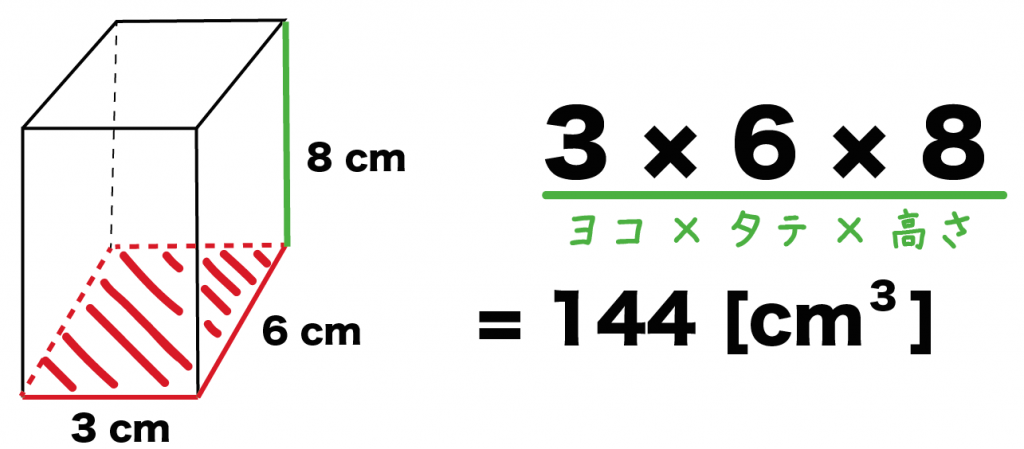
これで直方体の体積を計算できたね。
おめでとう。
直方体の体積の求め方はどうだったかな??
「タテ×ヨコ×高さ」
っていうシンプルな計算だけでいいんだ。
テスト前に復習してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。茶漬けを食べたいね。
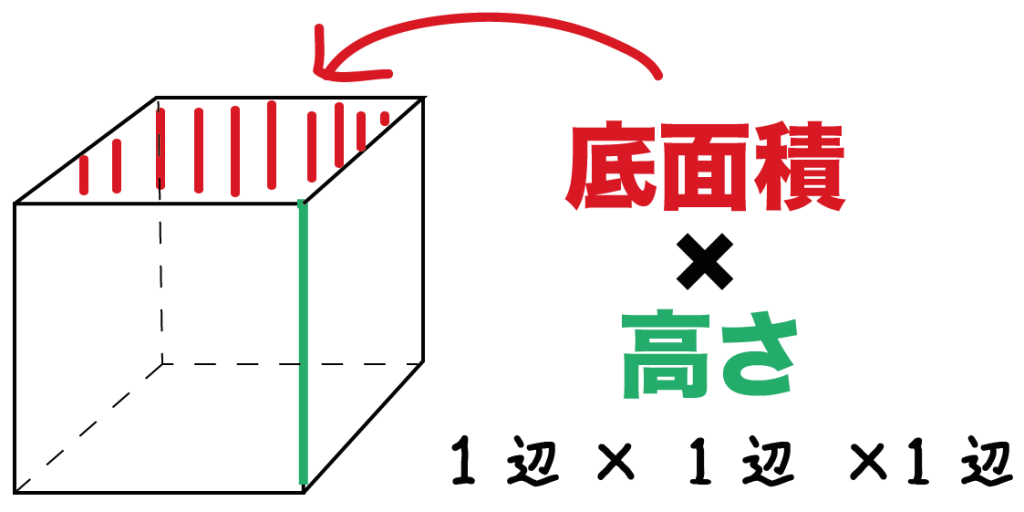
立方体の体積の求め方には公式があるんだ。
立方体の1辺の長さをaとすると、その体積は、
aの三乗
で求めることができるよ。
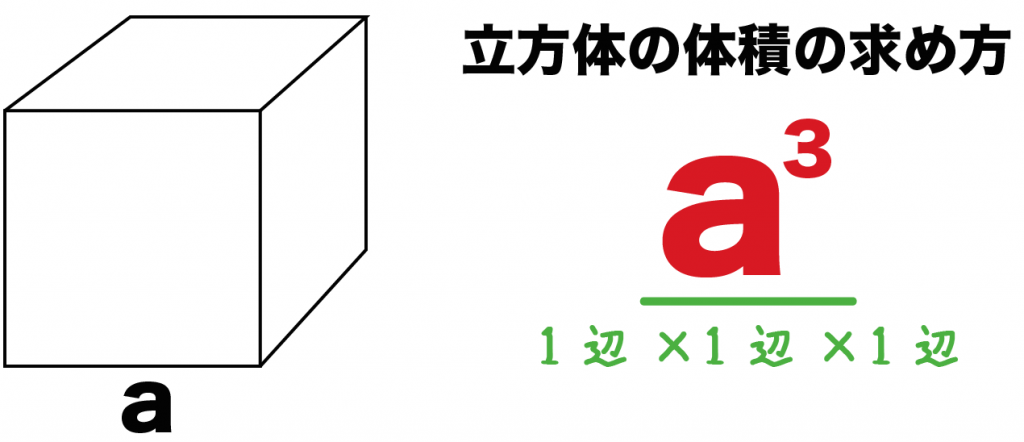
つまり、立方体の体積は、
1辺×1辺×1辺
ってことになる。立方体の1辺の長さを3回かけてやればいいんだ。
これは立方体だから特別というわけじゃなくて、
ただ単に、
底面積×高さ
という立体の体積の求め方通りに計算しているだけなんだよ。
どう??覚えやすくてむちゃくちゃ便利じゃない??
今日はこの計算公式をつかって実際に例題をといてみよう!
つぎの例題をみてみて↓↓
例題
1辺の長さが5 [cm]の立方体の体積を求めなさい。
立方体の体積は2ステップで計算できちゃうんだ。
立方体の「1辺」と「1辺」をかけてみよう!
立方体の各辺の長さは同じ。
ってことは、底面積を計算していることになるね。
例題の立方体の1辺の長さは「5cm」だから、
5×5
= 25[cm^2]
になる!
最後に立方体の1辺をかけてあげよう!
えっ。もう飽きたって??
耐えて!w
これで立方体の体積が計算できちゃうんだから!
なぜ、立方体の体積をもう一度かけるのか??
それは、さっきのステップで計算した「底面積」に「高さ」をかけることになるからだ。
つまり、立体の体積の求め方の基本の計算をしてるってことだね。
例題をみてみよう。
ステップ1で計算した値にもう一度、立方体の1辺をかけてみると、
5×5×5
= 125[cm^3]
になるね!
おめでとう!!
立方体の体積の公式はとってもシンプル。
1辺×1辺×1辺
だったね。
つまり、立方体の1辺の長さを3回かけちまえばいいんだ。
ホップ・ステップ・ジャンプ、
ジャブ・ジャブ・ストレート、
とほとんど同じさ。
1辺、1辺、1辺
というフレーズを口ずさみながら計算してみてくれ!
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。鉛筆削りが好きだね。
四角柱の体積の求め方の公式って知ってる??
四角柱の底面積をS、高さをhとしてあげると、
四角柱の体積は、
Sh
で計算できちゃうんだ。
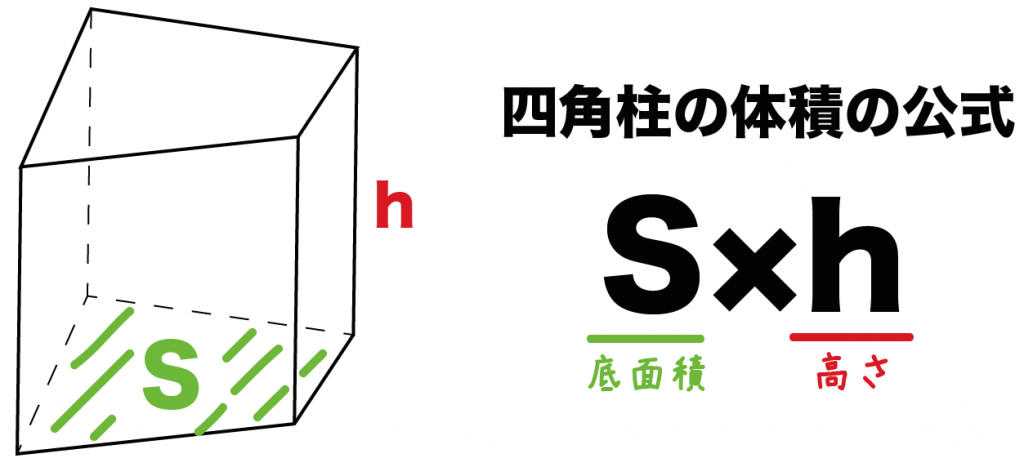
つまり、
底面積×高さ
っていう掛け算だね。なんだかいけそうな気がするっしょ??。
今日はこの公式をつかって実際に例題をといてみよう!
つぎの例題をときながらみていこう。
例題
つぎの四角柱の体積を求めてね。
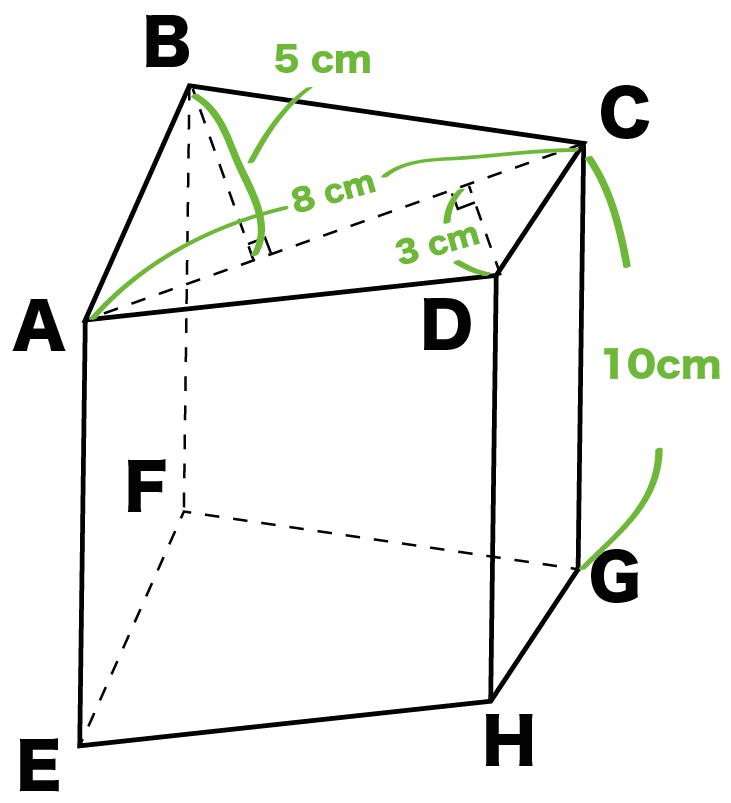
まずは四角柱の底面積を求めよう。
四角柱の底面は「四角形」。公式とかをつかって計算してみてね。
例題の四角柱の底面はちょっと普通じゃない四角形だね。
台形でもないし、ひし形でもないし、もちろん正方形でもない。
こういう四角形は、
2つの三角形の面積を求めて足し合わせる
という作戦で計算してみよう!
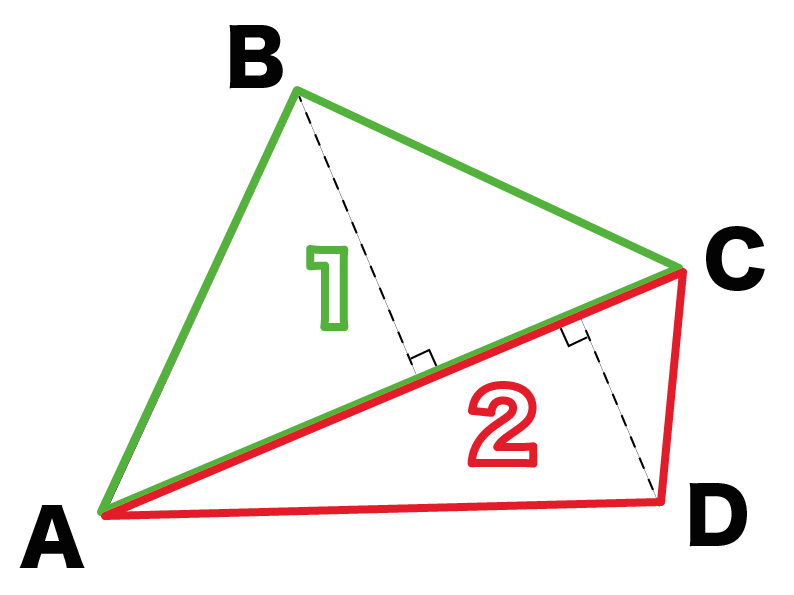
例の底面は緑の「三角形 (1)」、赤の「三角形 (2)」に分割することができるね。
緑と赤の三角形の面積はそれぞれ、
だから、
この四角柱の底面積はその合計の32[cm^2]になるね。
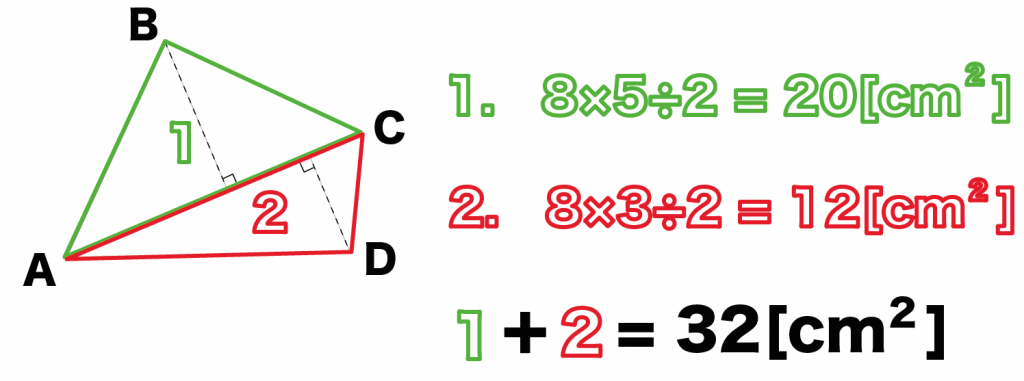
さっき計算した「底面積」に「高さ」をかけてあげちゃおう。
そうすれば四角柱の体積が求まるはずだ。
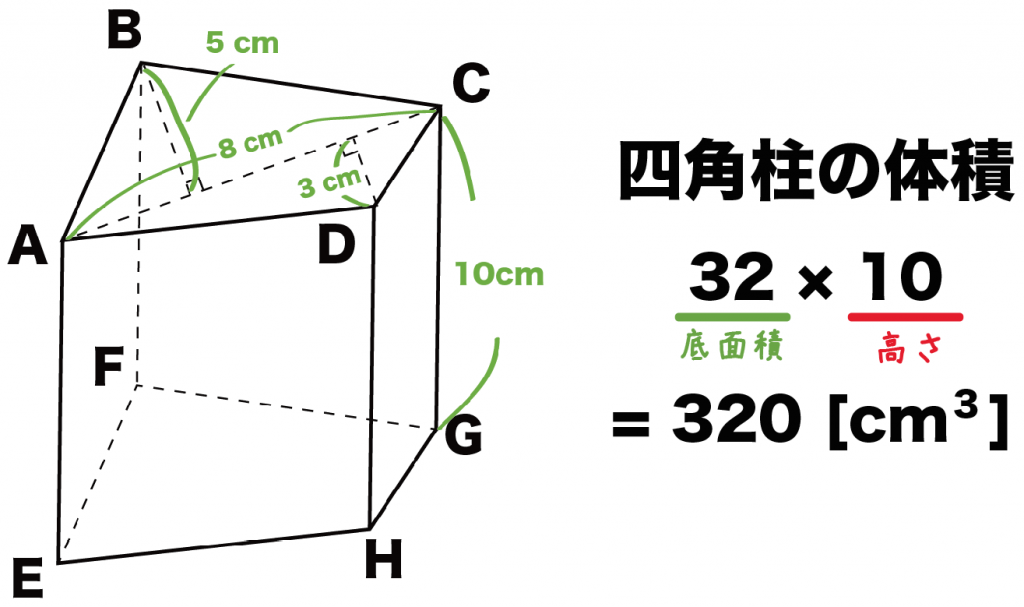
例題の四角柱の高さは10[cm]。
これを底面積である32[cm^2]にかけてやると、
32×10
= 320[cm^3]
になるね。
おめでとう!これで四角柱の体積を計算できたね。
四角柱の体積の求め方はどうだった??
底面の四角形の面積を計算して、それに高さをかけるだけだね。
テストに四角柱の体積がでてきたらバシバシといていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。青い空が好きだね。
正四角錐の体積の求め方には公式があるんだ。
正四角錐って底面が正方形で、先がとんがっている立体のことだったよね。
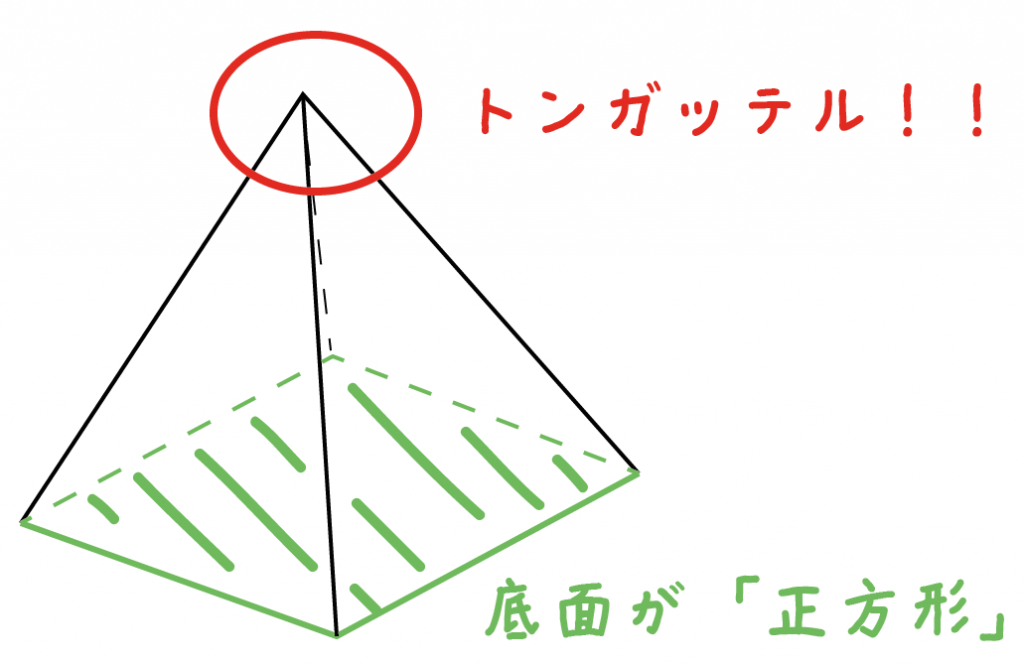
底面の1辺の長さをa、高さをhとすると、体積はつぎのようにあらわせるよ。
1/3 a²h
つまり、
(底辺の1辺)×(底辺の1辺)×(正四角錐の高さ)÷3
ってことだね。
今日は、この計算公式をどうやって使うのか??
ということをわかりやすく解説していくよ。
正四角錐の体積は3つのステップで計算できちゃうんだ。
例題をときながらみていこう!
底辺の1辺の長さが6 [cm]、高さが8 [cm]の正四角錐の体積を求めてください。
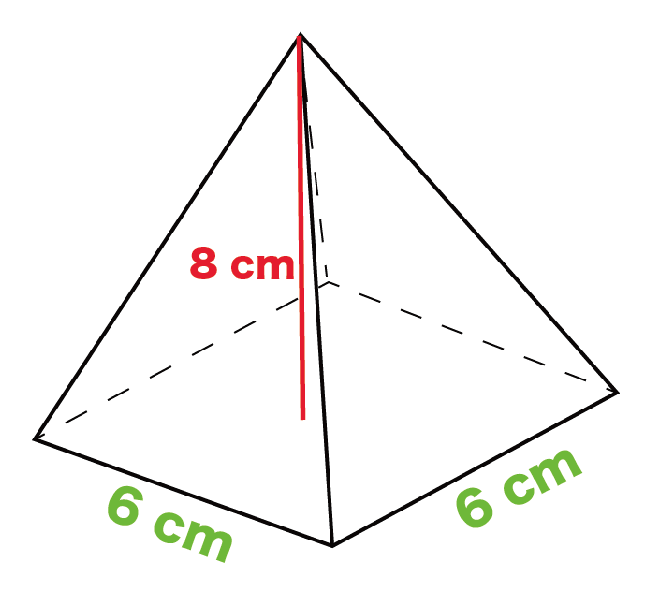
まずは正四角錐の底面積を求めてみよう。
正四角錐の底面は「正方形」だよね?? 正方形の面積を「1辺×1辺」という公式をつかって計算してくれ。

例題でいうと、
底面の正方形の1辺は6[cm]だよね。だから、底面積は、
6×6 = 36[cm²]
になる。
さっき計算した底面積に「高さ」をかけてみよう!
例題の正四角錐の高さは8 [cm]だから、
36×8
= 288[cm³]
になるね。
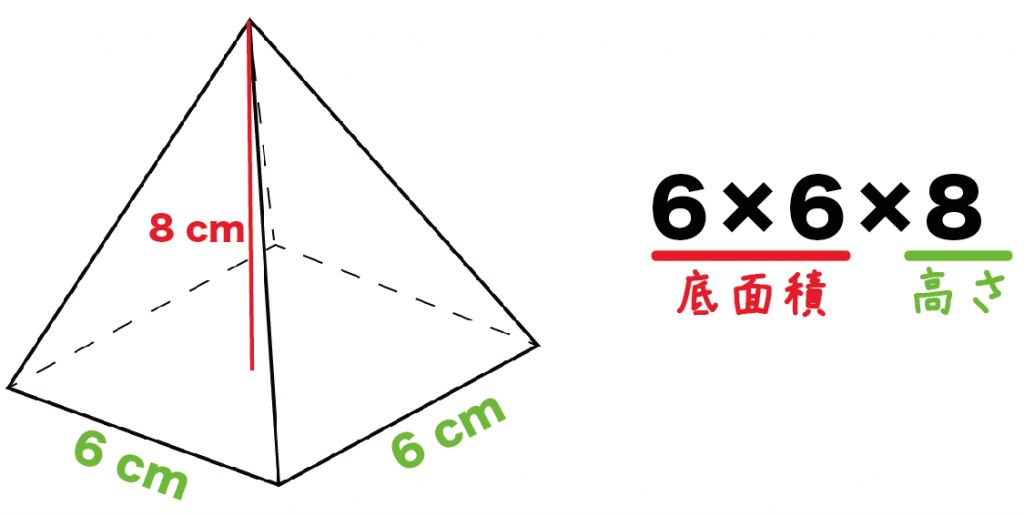
計算ミスに気をつけてね。
底面積に高さもかけたし・・・
と安心してはダメ。
先がとんがっているタイプの「錐体」では、体積を求めるときに必ず「1/3」をかけなきゃいけないんだ。
えっ。なぜ1/3をかけるのかって??
それは円錐の体積の求め方でも触れたけど、
高校数学でならう「積分」を使わないと説明できないんだ。
だから、中学数学ではとりあえず、
先がとんがっている立体の体積の計算は「底面積×高さ×1/3」になる
って覚えておけば問題ないよ。
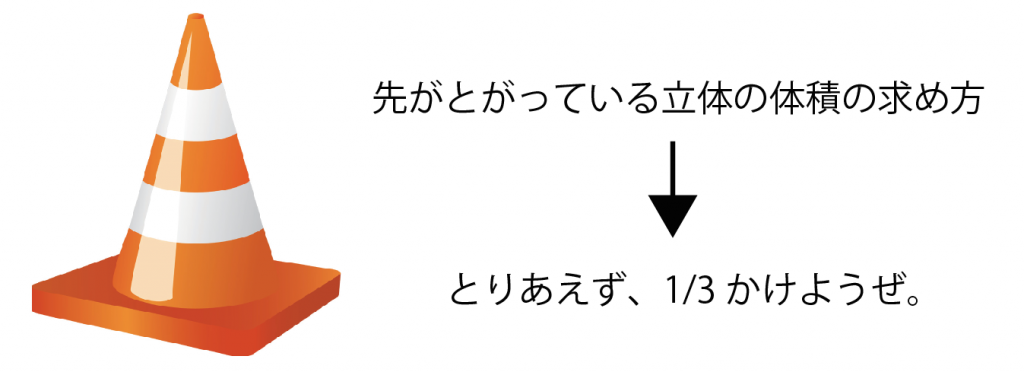
だから例題の正四角錐の体積は、
6×6×8×1/3
= 96[cm³]
になるんだ。
おめでとう!これで正四角錐の体積を計算できたね。
正四角錐の体積の公式はどうだった??
底面積×高さ×1/3
という計算をゆっくりしてみてね。テスト前に復習しておくと心強いかも!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。登山で日焼けしたね。
三角柱の体積の求め方には公式があるんだ。
三角形の底辺の長さをa、底辺からの高さをb、立体の高さがhっていう三角柱を想像してみて。
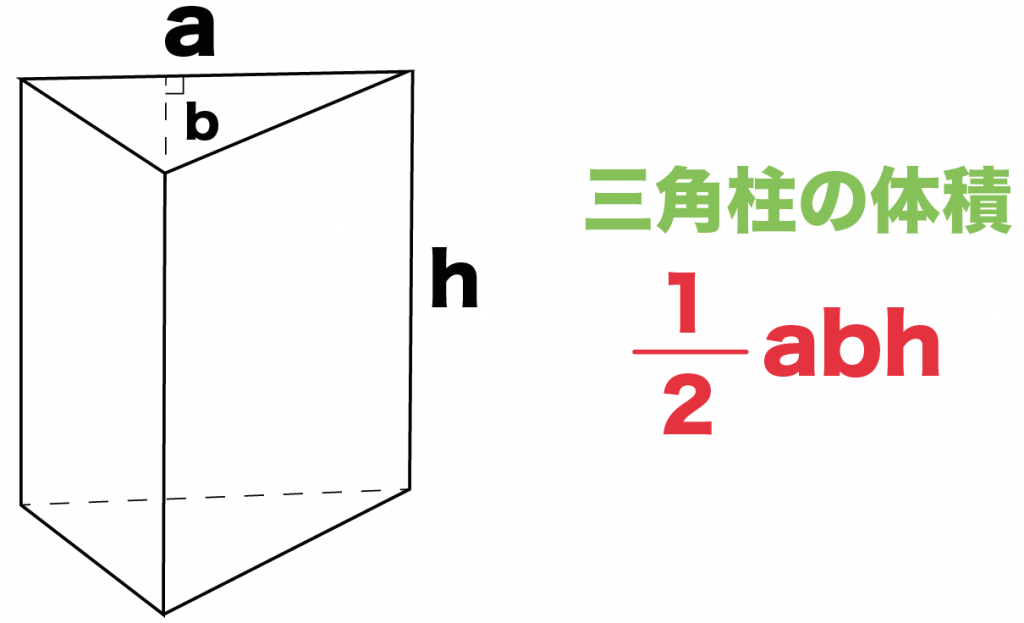
このとき、
三角柱の体積は、
1/2 abh
で求めることができるんだ。
つまり、
1/2 ×(底面の底辺)×(底辺からの高さ)×(三角柱の高さ)
ってことになるね。
この公式では何も特別なことをやってるわけじゃない。
ただ、
底面積×高さ
という「角柱の体積の公式」を使っているだけなんだ。
今日はこの公式をわかりやすく解説していくよ。
よかったら参考にしてみてね!
三角柱の体積は2ステップで計算できちゃうんだ。
つぎの例題をときながら求め方を確認していこう。
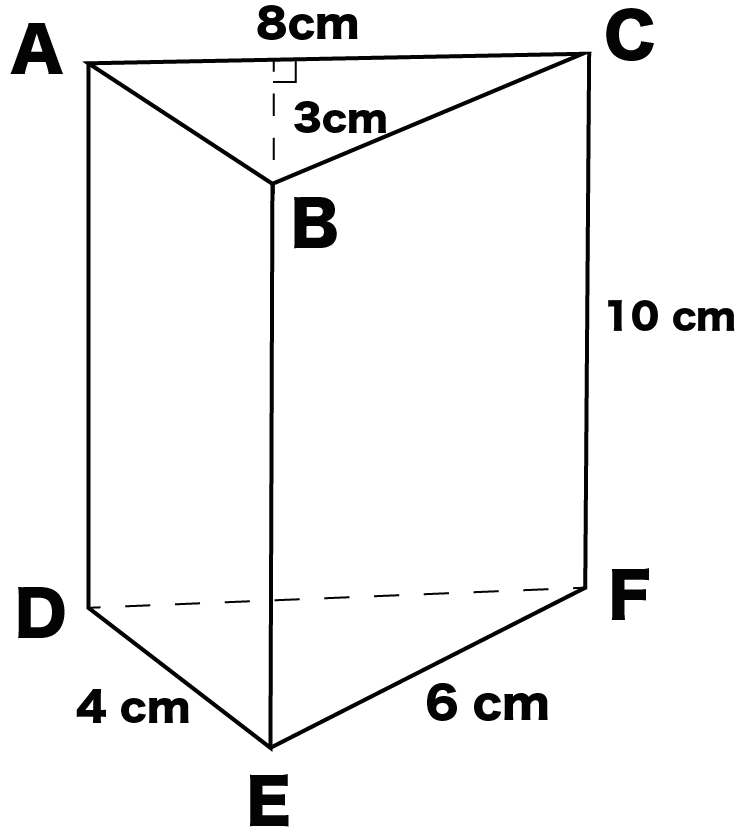
まずは三角柱の底面積を求めてみよう。
三角柱の底面は「三角形」であるはずだから、
底辺 × 高さ× 1/2
で面積をゲットできるよね??
例題でいうと、
底辺の長さが「8 cm」、高さが「3 cm」だから、
8×3 × 1/2
= 12 [cm^2]
になるね!
さっき計算した「底面積」に「三角柱の高さ」をかけてみよう!
なぜなら、
底面積×高さ
を計算すると立体の体積を求めることができるからね。
例題でいうと、
Step1で計算した底面積は10[cm^2]、三角柱の高さは10[cm]だから、
三角柱ABCDEFの体積は、
12×10
= 120[cm^3]
になるんだ。
これで三角柱の体積を求めることができたね!
三角柱の体積の求め方はどうだった??
三角柱の体積の求め方はとってもシンプル。
「底面積×高さ」という計算をしてやるだけだよ。
ゆっくりと慎重に計算すれば大丈夫だから、どんどん三角柱の体積を計算していこう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。ピーナッツが食べたい気分だね。
三角柱の表面積を計算するときは公式を使ってみよう。
三角柱のスペックが、
のときを考えてみてね。
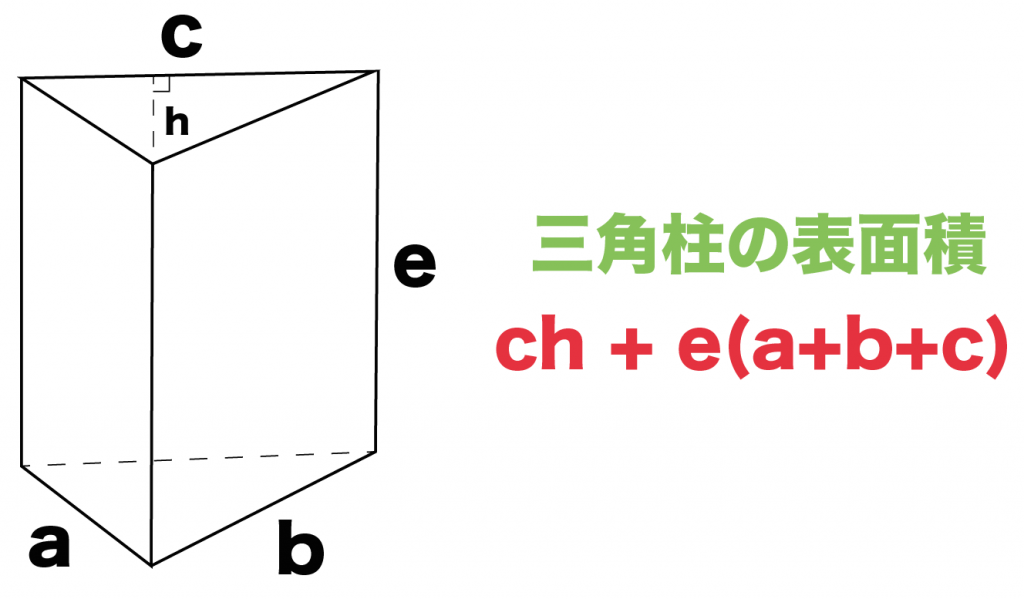
この三角柱の表面積は、
ch + e (a+b+c)
という公式で計算できちゃうんだ。
何をやっているかというと、
(底面の三角形の面積)×2 + (側面積)
という表面積の基本計算をしているだけだよ。
えっ。
ちょっとわかりづらいって??
そうだね。
今日は、三角柱の表面積をわかりやすく解説していくよー!
公式がよくわからんときに参考にしてみて。
表面積は3つのステップで求めることができるんだ。
つぎの例題をときながら解説していくよ。
例題
底面の三角形の辺の長さが8cm、4cm、6cm、
底辺を8cmとしたときの高さを10cmとする。
この三角柱ABCDEFの表面積を求めなさい。

まずは三角柱の底面積を計算しよう!
三角柱の底面積はもちろん「三角形」。
三角形の面積の求め方は「底辺×高さ×1/2」だったよね。ここでもこの公式を使ってみよう。
例題の三角柱は底辺をACとしたとき、高さが 3 [cm]である、ということはわかっているので、
底面積は、
8×3×1/2
= 12[cm^2]
となるね。
つぎは三角柱の側面積を計算してみよう。
三角柱の展開図をみるとわかるのは、
1つの大きな長方形が側面になっているということだ。
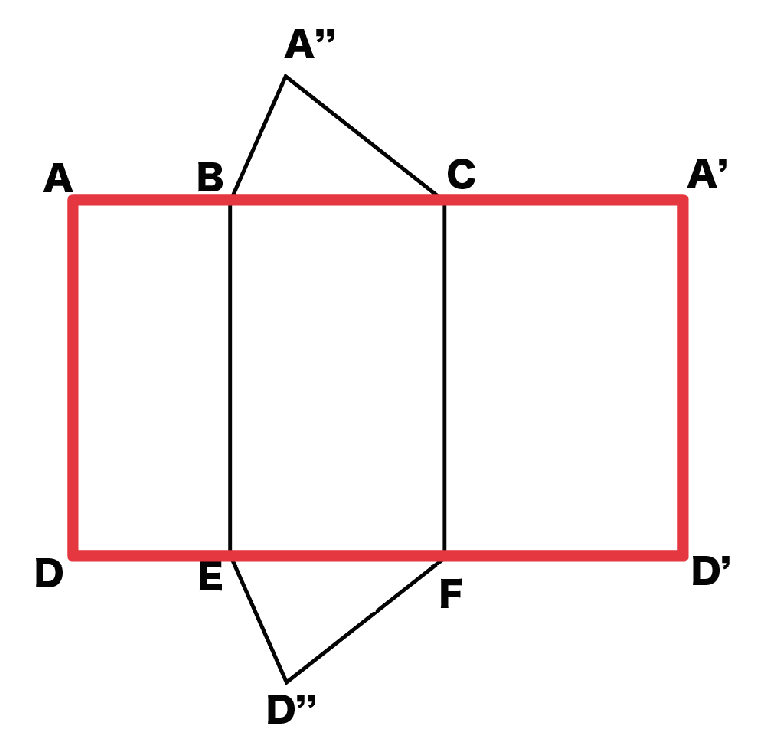
この長方形のタテの長さは「三角柱の高さ」。
ヨコの長さは「底面の辺の長さをすべて足し合わせたもの」になっているよね。
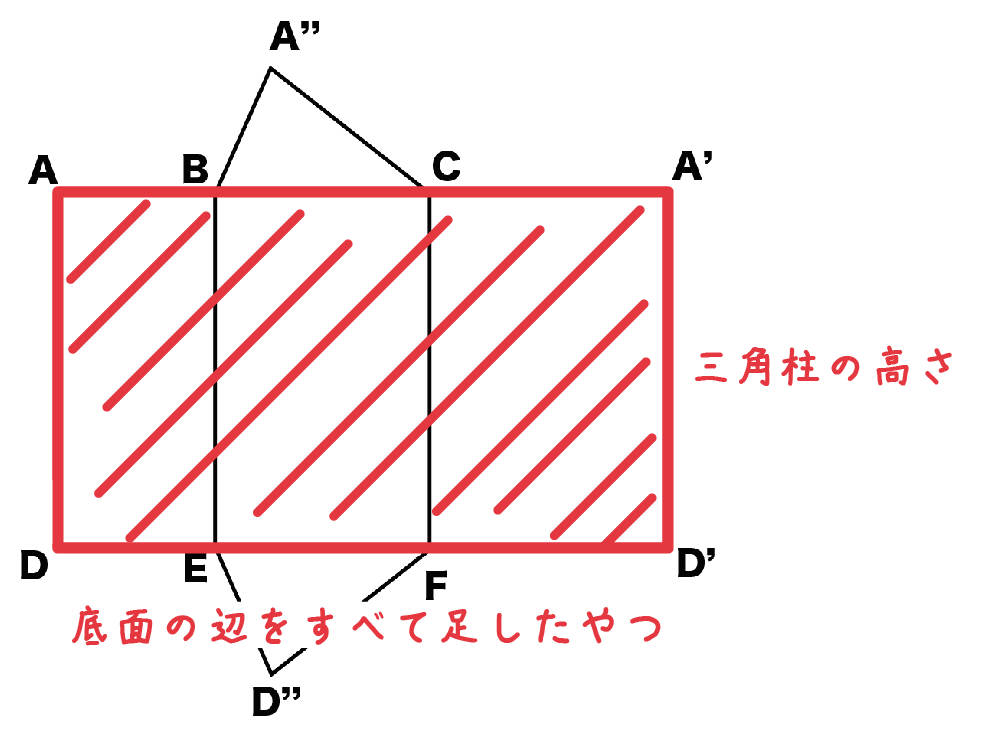
長方形の面積の求め方は「タテ×ヨコ」だから、三角柱の側面積の求め方は、
「底面の辺の総和」×「三角柱の高さ」
になるよ。
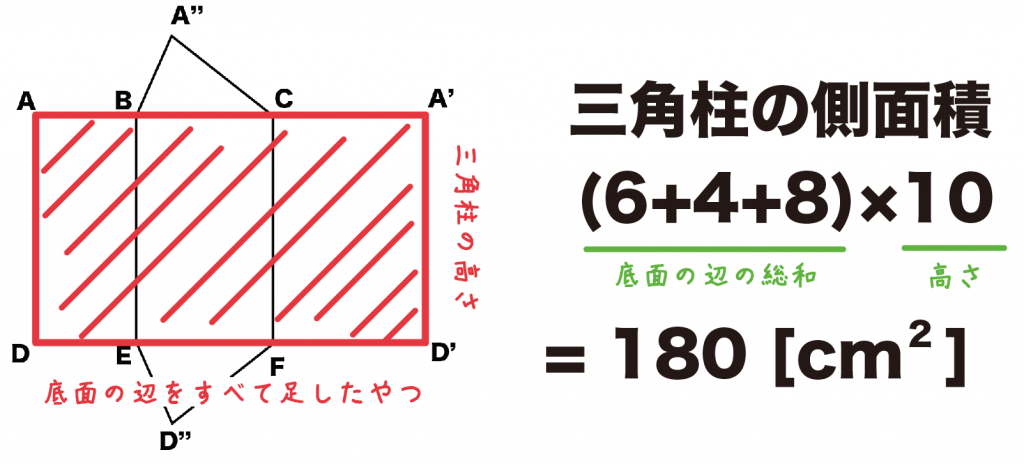
例題でいうと、
だから、三角柱の側面積は、
(6+4+8)×10
= 180[cm^2]
になるよ。
さあ、いよいよ三角柱の表面積を計算しちゃうよ。
三角柱の展開図をみてみると、
「三角形2つ」と「側面の長方形」でなりたっていることがわかるよね??
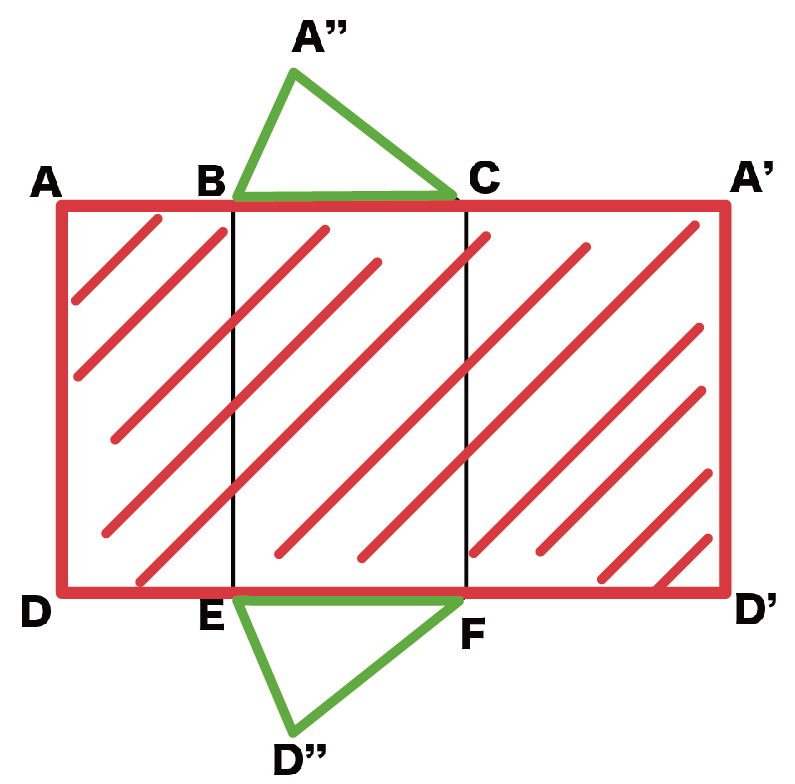
だから、三角柱の表面積を計算するには、
「底面積を2つ」と「側面積」を足せばいいんだ。
例題をみてみよう。
「底面積」は12[cm^2]、「側面積」は180[cm^2]だったよね??
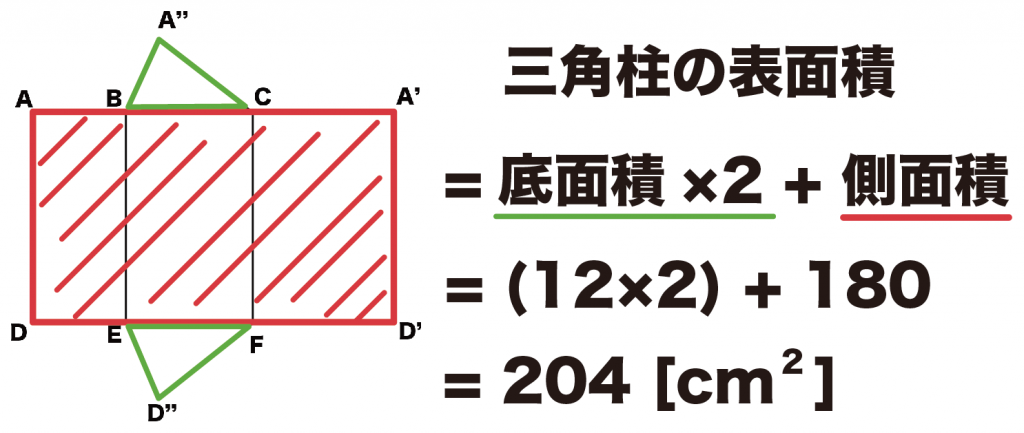
よって、
三角柱の表面積は、
12×2 + 180
= 204[cm^2]
になるね。
三角柱の表面積は、
底面積×2 + 側面積
で求めることができる!
これさえ覚えておけば、あとは簡単な計算をするだけだね。
三角柱の表面積の宿題がでたらちゃちゃっと瞬殺しちゃおう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。天せいろはうまいね。
立方体の表面積の求め方には公式があるって知ってた??
立方体の1辺の長さをa [cm]とすると、
表面積は「6aの2乗」で計算することができるんだ。

つまり、
立方体の1辺を2回かけて、それを6倍すればいいってことだね。
今日は、この公式をゆっくり解説していくよ。
求め方がよくわからん!ってときに参考にしてみて。
つぎの2ステップで立方体の表面積は計算できちゃうよ。
例題をときながらみていこう。
例題
1辺の長さが6cmの立方体の表面積をもとめてね。
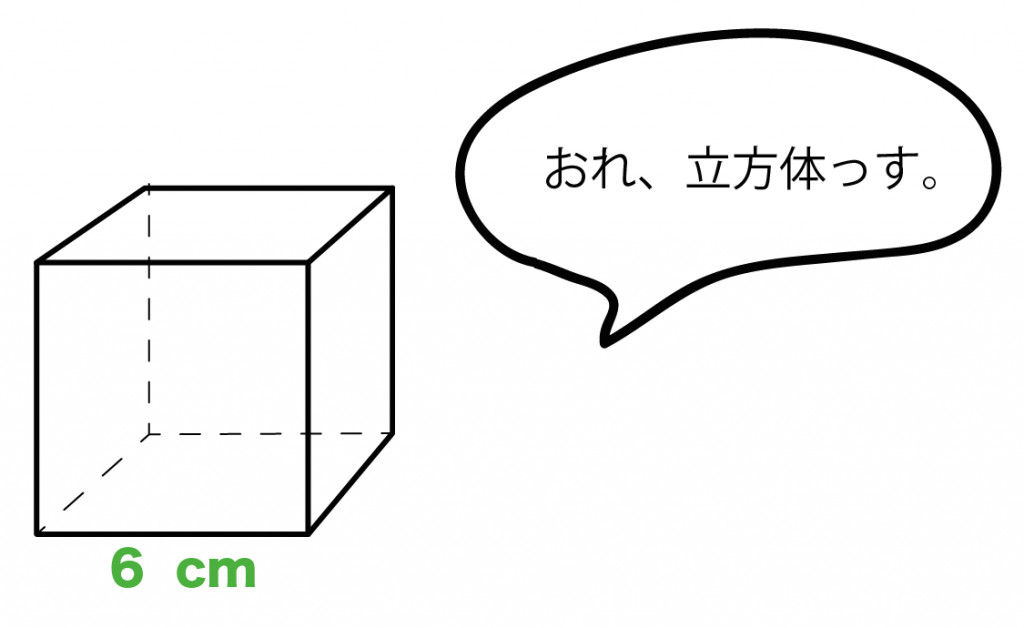
まずは1つの面の面積を求めてみよう。
立方体はすべての面が「正方形」だったよね??
だから、一つの面の面積は「1辺×1辺」で求めることができる。
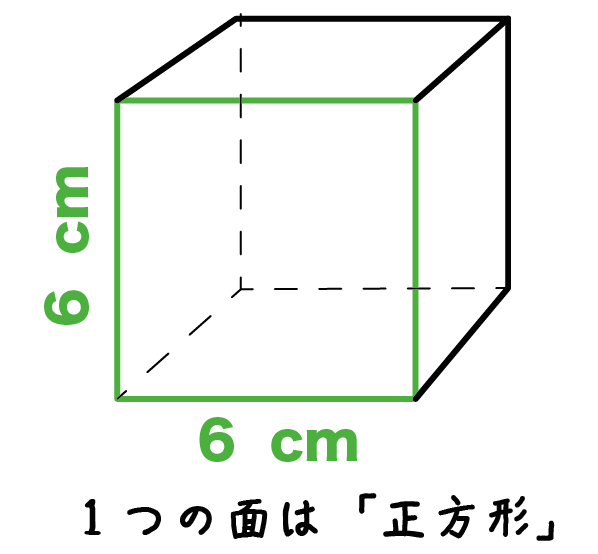
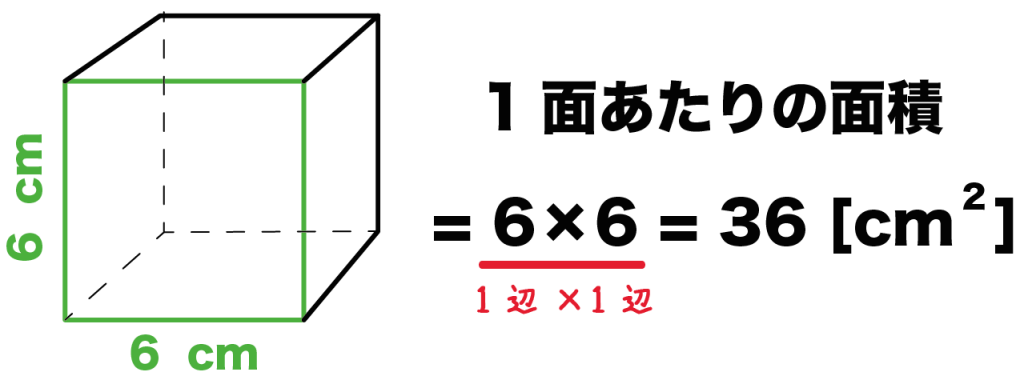
例題でいうと、
立方体の1辺の長さは「6cm」だから、1つの面の面積は、
6×6
= 36 [cm^2]
になる!
Step1で計算した「1つの面の面積」を6倍してみよう。
えっ。なぜ6倍するのかって??
それは立方体の展開図をかいてみれば一発でわかることなんだ。
立方体の展開図をみてみると、
正方形が6つあるでしょ??
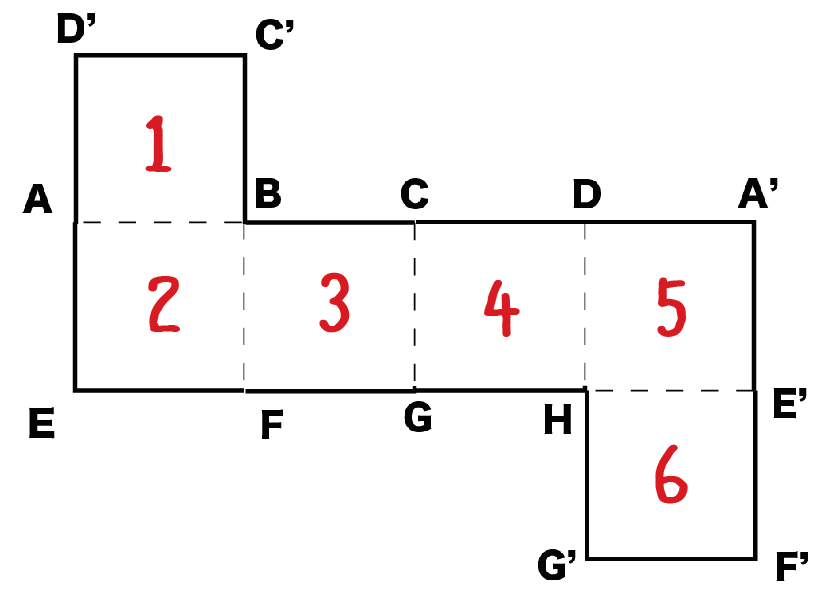
ってことは、立方体の表面積を計算するときは、
1つの面の面積を6倍してあげればいい!
ってことになるね。
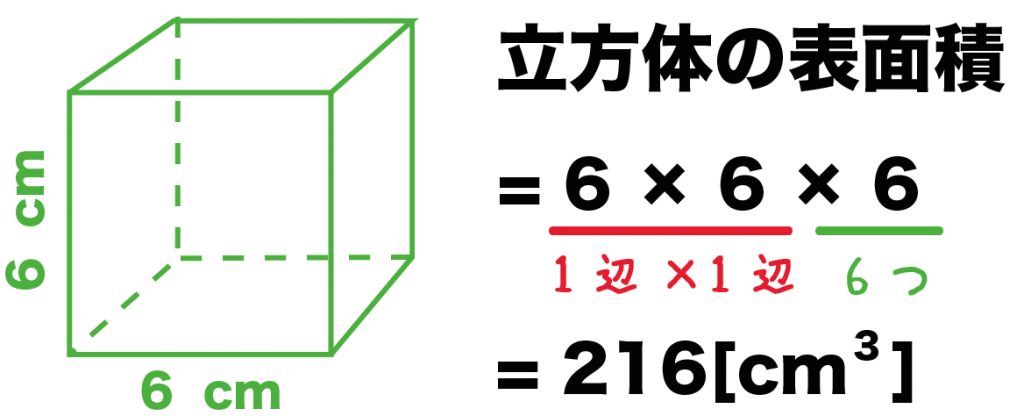
さっきの例題だと、
1つの面の面積は36[cm^2]だったから、そいつを6倍した
216[cm^3]
が表面積になるね。
おめでとう!!
立方体の表面積の求め方は簡単。
1辺×1辺×6
でいいんだ。辺と辺をかけてそいつを6倍するだけ。
テストに立方体の表面積の求め方がでてきたらバンバンといてみよう!!
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。ティッシュは便利だね。
直方体の表面積の求め方にも公式があるよ。
タテの長さをa、ヨコの長さをb、高さをcとすると、
2(ab+bc+ac)
で直方体の表面積が計算できちゃうんだ。
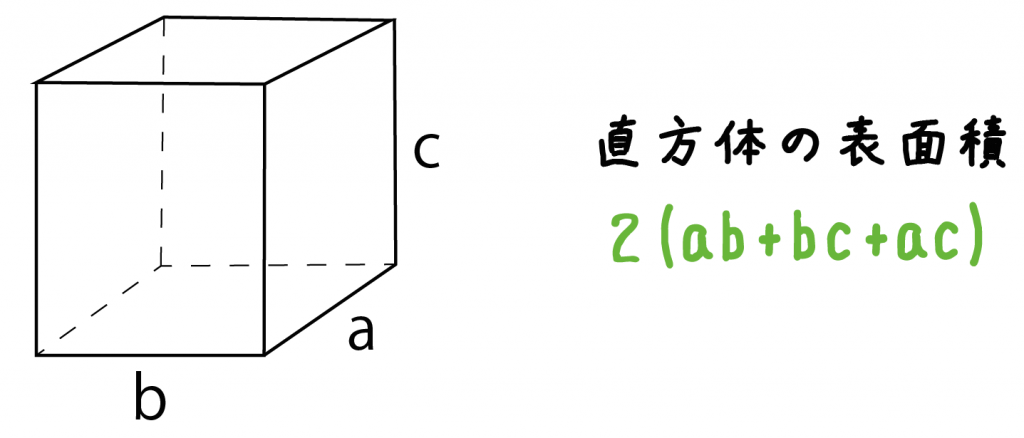
つまり、
「タテ」と「ヨコ」と「高さ」をそれぞれかけたものを足して、それを2倍すればいいってこと!
どう?? むちゃくちゃ便利じゃない??
だがしかし。
直方体の表面積の公式をテストで忘れちゃうこともある。
今日はそんなときに備えて、
公式に頼らない「直方体の表面積の求め方」を3つのステップで解説していくよ。
テスト前に確認してみてね。
つぎの例題ときながらみていこう。
例題
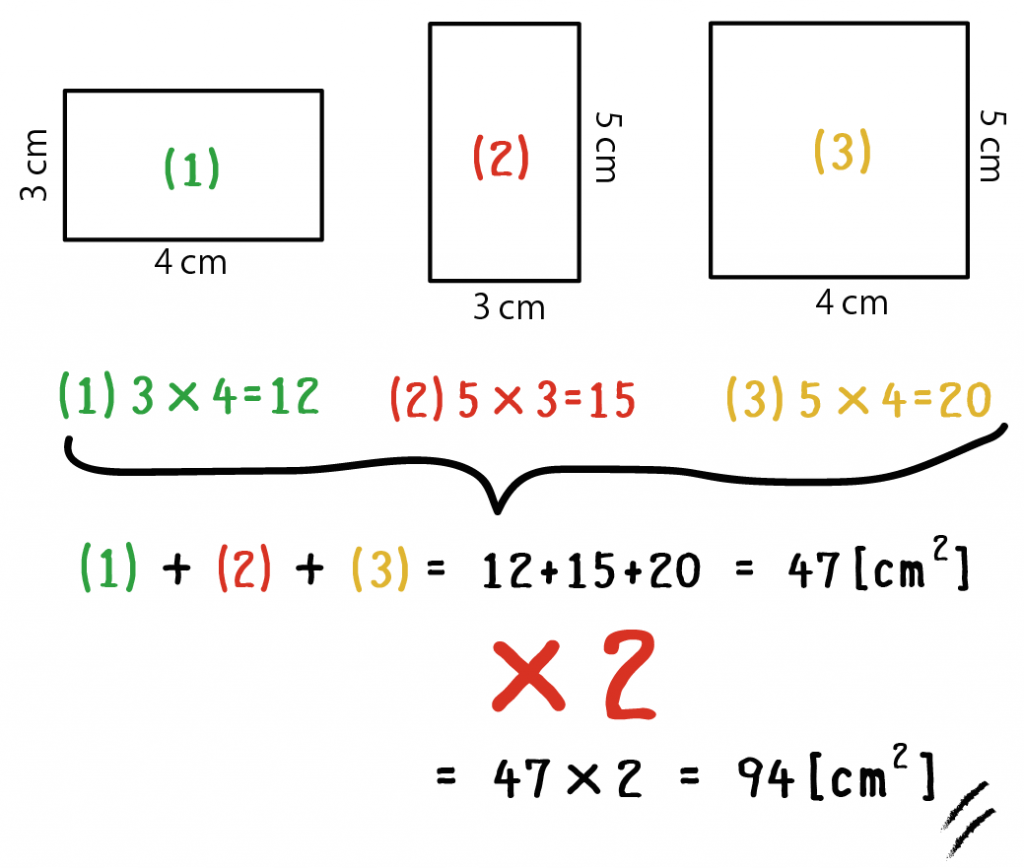
タテ 4cm、ヨコ 3cm、高さ5cmの直方体の表面積を計算してみな!
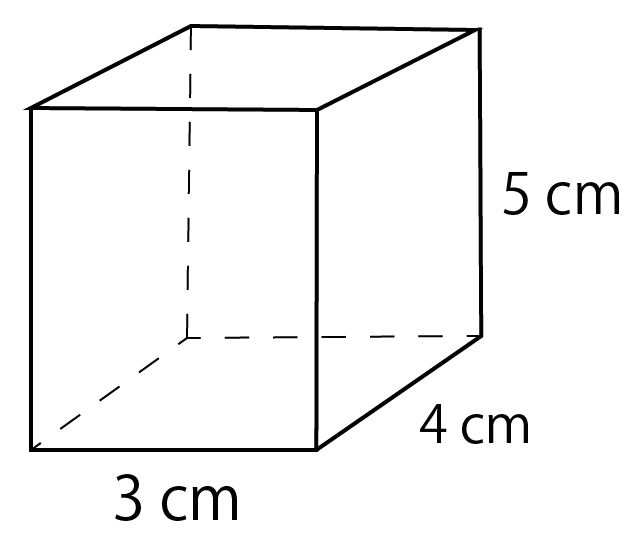
直方体の表面積は3つの長方形でなりたっているんだ。
まずはそいつらの面積を計算してくよ。
えっ。なぜ3種類なのかって??
それは、直方体の展開図をかいてみるとわかるんだ。
展開図をよーくみてみると、
(1)、(2)、(3)の3種類の長方形しかないことがわかる。
まずはこいつらの面積を計算してあげよう。
長方形の面積の求め方は「タテ×ヨコ」だから、
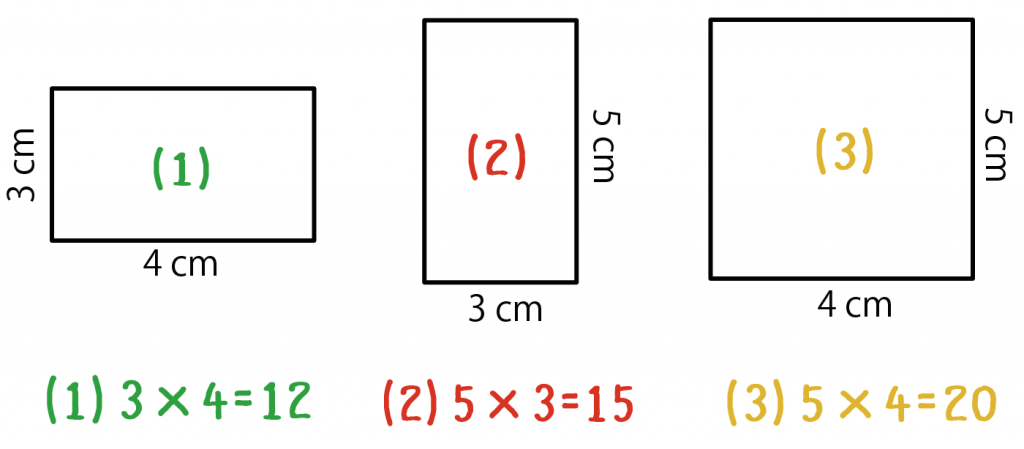
になるね!
3つの長方形の面積を足し合わせてみよう!
12 + 15 + 20
= 47
って感じで!
最後は3つの長方形の合計を2倍するよ。
なぜ2倍するのか??
それは、
直方体の展開図には3種類の長方形が2つずつあるから
なんだ。
例題でいうと、3つの長方形の面積の合計は「47平方センチメートル」だったね??
こいつを2倍してやると、
94平方センチメートル
になる。
これで直方体の表面積を計算できたね!おめでとう。
直方体の表面積の公式はどうだった??
3種類の長方形の面積を足して、それを2倍するだけ!
直方体の表面積の問題がでたらバンバン解いていこう。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。犬の散歩が趣味だね。
円錐の体積の求め方の公式は、
底面積×高さ×1/3
だったよね。
もう少し詳しくかいてあげると、
半径×半径×円周率×円錐の高さ×1/3
になるんだ。
これなら3秒で円錐の体積を計算できちゃいそうだね。
ただ、そのスピード感について来れないときもあるだろうから、今日は、円錐の体積の求め方をチョーゆっくり公式をつかってといてみるよ。
「円錐の体積の求め方がどうしてもわからん!」
ってなったときに参考にしてみてね!
円錐の体積の求め方はつぎの3ステップをで計算できちゃうよ。
つぎの例題をときながらみていこう!
半径3cm、高さ10cmの円錐の体積を計算して。
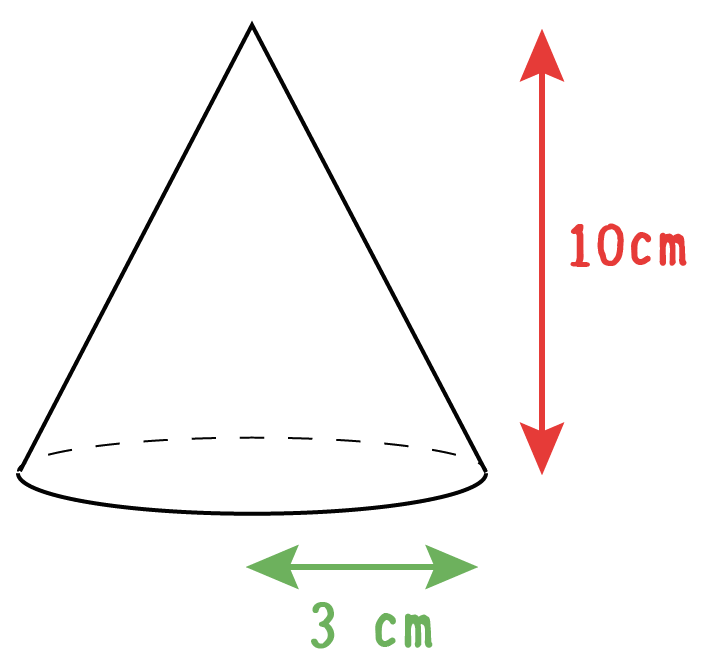
まずは円錐の底面積を計算してみよう。
円錐の底面は「円」になっているね。
ってことは、円の面積の公式をつかって、ちゃちゃっと面積をだしてやればいいんだ。
円の面積の求め方は、
半径×半径×円周率
で求められるよね??
だから例題の円錐の底面積は、
3×3×π= 9π
となるんだ。
つぎは「円錐の高さ」を底面積にかけてみよう。
例題の円錐の高さは10cmなので、
9π×10= 90π
になるっ!
いよいよ最後のステップ。
Step2で求めた「底面積×高さ」の値に「1/3」をかけてみよう。
例題でいうと、「底面積×高さ」は「90π」だったから、
最終的な円錐の体積は、
90π×1/3=30π
になる!
おめでとう。これで円錐の体積を計算できるようになったね。
えっ。なんで「1/3」をかける必要があるのだって?!?
その理由は高校数学で勉強する「積分」を使えば説明できるんだけど、完全に中学数学の範囲をこえているんだ。
とりあえず、中学数学では、
錐体(先がとんがってるやつ)の体積を求めるときは「1/3」をかける
ということを覚えておこう。
だから、三角錐の体積を求めるときも「1/3」をかけるんだ。
円錐の体積の求め方はどうだったかな??
底面積×高さ×1/3
という公式は意外とシンプルだったよね。
最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。
分数がややこしかったら、「÷3」をするって覚えてもいいね。
この公式をつかってじゃんじゃん円錐の体積を計算していこう!
円錐の体積の求め方をマスターしたら、次は「円錐の表面積の求め方」を勉強してみよう。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。鶏肉は煮るとウマいね。
正四角錐って、
底面が「正方形」の錐体のこと
だったよね??
つまり、底面が正方形で、先がとんがっている立体ってことだ。

そんな正四角錐の表面積は
(底面の正方形)+(側面の三角形)×4
で求めることができるよ。
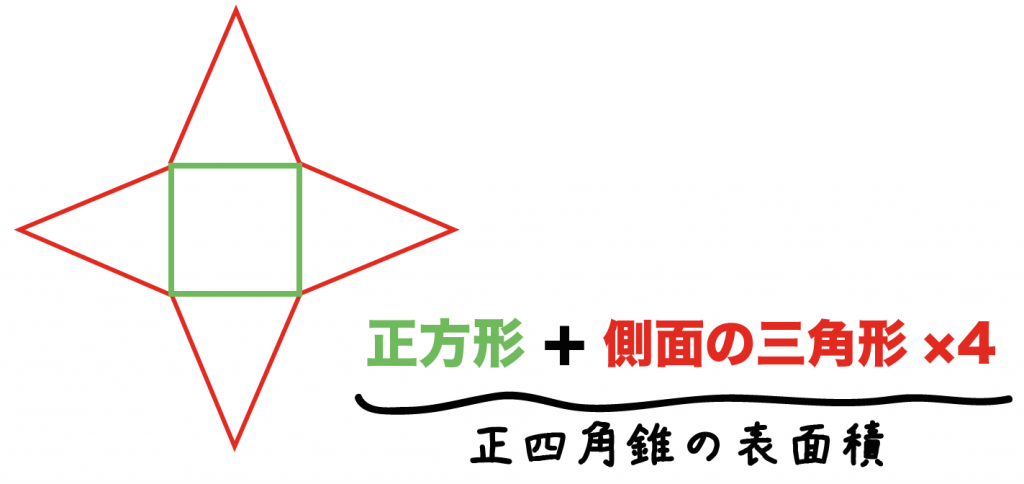
だって、正四角錐の展開図が「正方形1つ」と「三角形4つ」で成り立っているからね。
つまり、
「底面の1辺の長さ」と「側面の三角形の高さ」がわかっていれば計算できるってわけさ。
えっ。どんな問題がわからないから怖すぎるだって!?
そ、そんなキミでも大丈夫。
じつは、中学数学ででてくる「正四角錐系の問題」ってだいたい次の3つのパターンになるんだ。
それぞれの求め方についてゆっくりみていこう。
いちばん簡単なパターン。中学1年生でもとける問題だね。
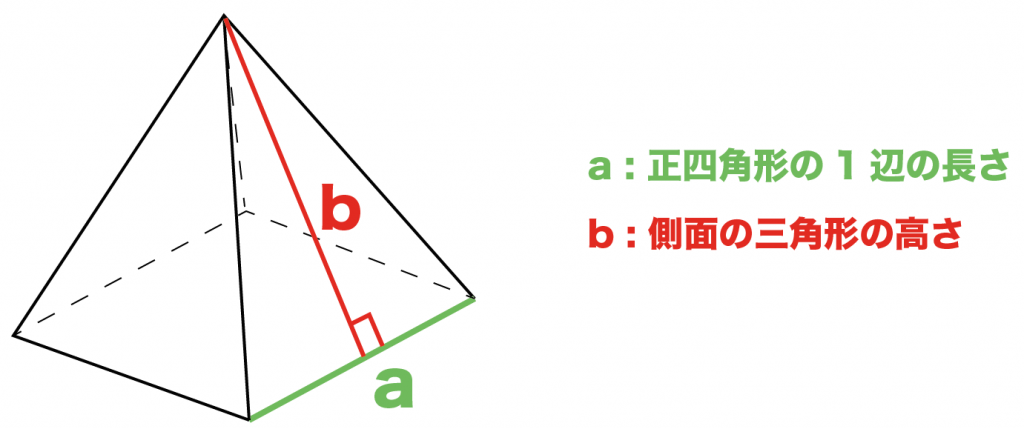
「底面の1辺の長さ」と「側面の三角形の高さ」がわかっているから、
「底面の正方形」+「側面の三角形」×4
を計算すればいいんだ。
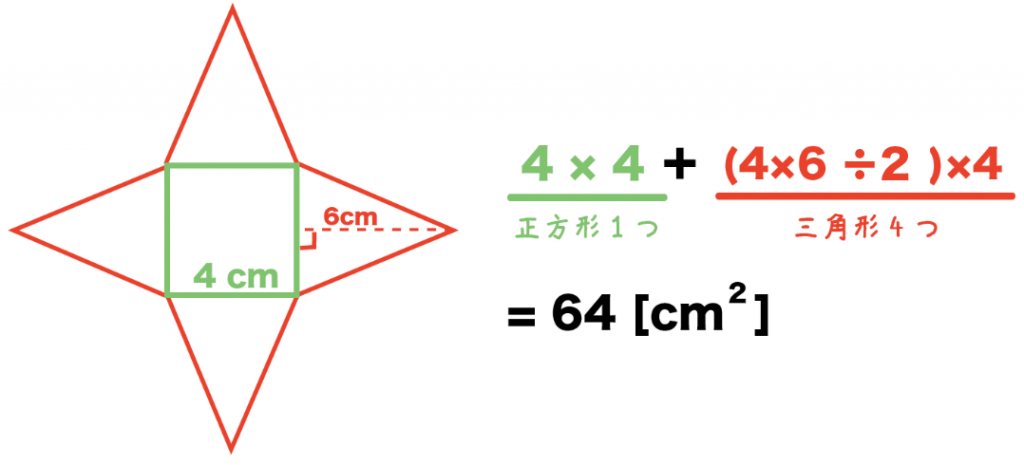
たとえば、底面の1辺の長さが4cm、側面の長さが6cmだとしよう。
 正四角錐の展開図は「底面の正方形1つ」と「側面の三角形4つ」で構成されているね。
正四角錐の展開図は「底面の正方形1つ」と「側面の三角形4つ」で構成されているね。
よって、正四角錐の表面積は、
( 4×4 ) + ( 4×6÷2 ) × 4
= 64 [cm²]
になる。
中1数学ではこの種類しか出題されないよ。
しっかり押さえておこう。
2つ目のパターンは、
「正方形の1辺」と「側面の三角形の辺の長さ」がわかっているパターンだ。
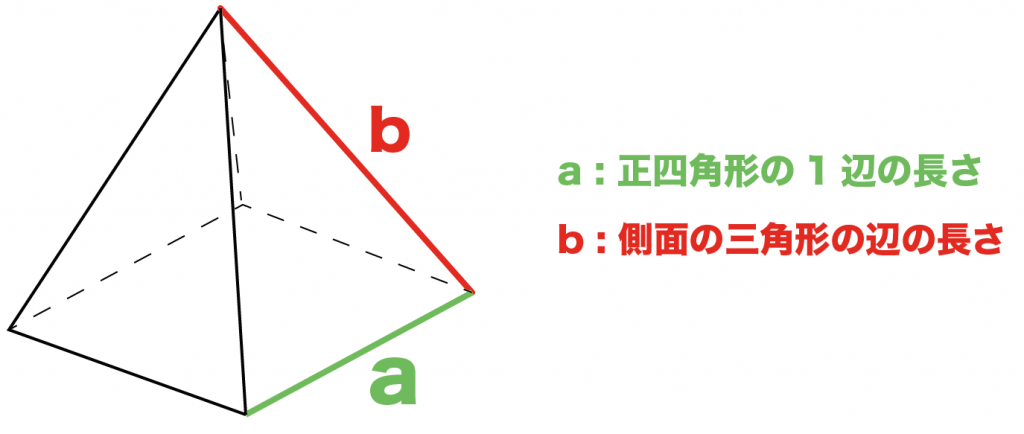
正四角錐の表面積の求め方って、
側面の三角形の高さ
さえわかっていれば計算できちゃう。
ってことは、「正方形の辺の長さ」と「側面の三角形の辺の長さ」から「側面の三角形の高さ」を計算しちゃえばいいってことになるね。
たとえば、
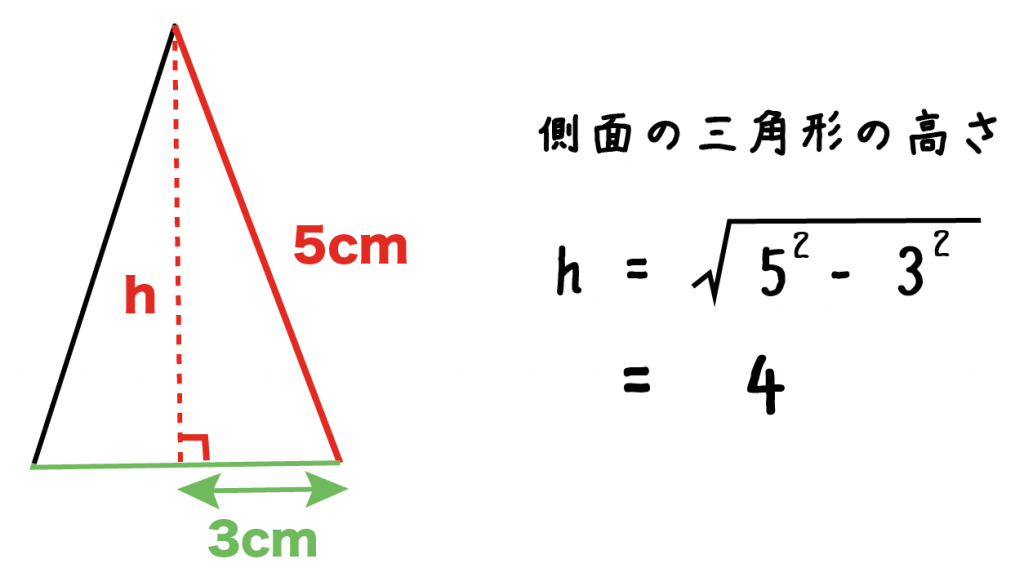
底面の1辺の長さが「6cm」、側面の三角形の辺の長さが「5cm」の正四角錐があったとしよう。
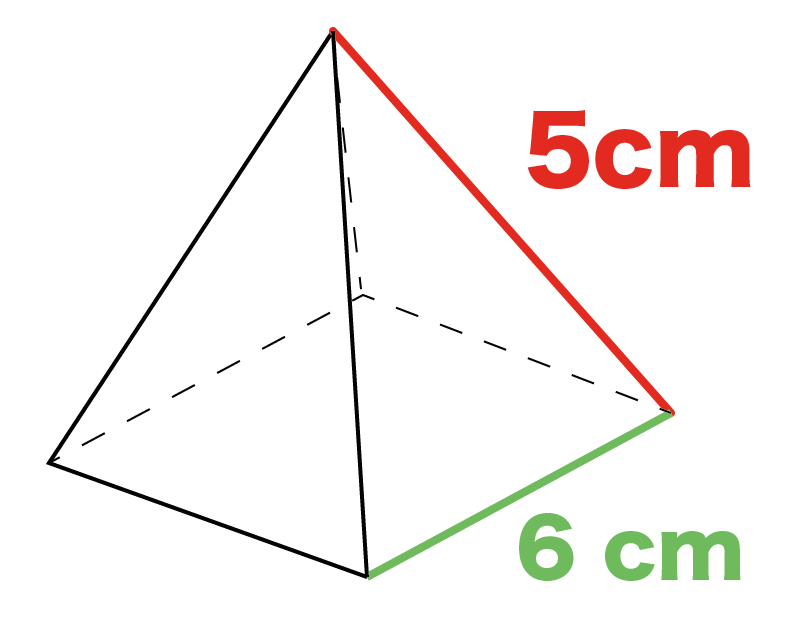
側面の三角形は二等辺三角形だから、頂点から底辺にひいた垂線は垂直二等分線になっているね。
側面の三角形の高さhは、三平方の定理をつかうと次のように計算できる。
√(5² – 3²)
= 4
側面の三角形の高さがわかったらもう大丈夫。
正四角錐の表面積は、
「底面の正方形」+「側面の三角形」×4
だったよね?? これも1つめのパターンと同じように計算してやると、
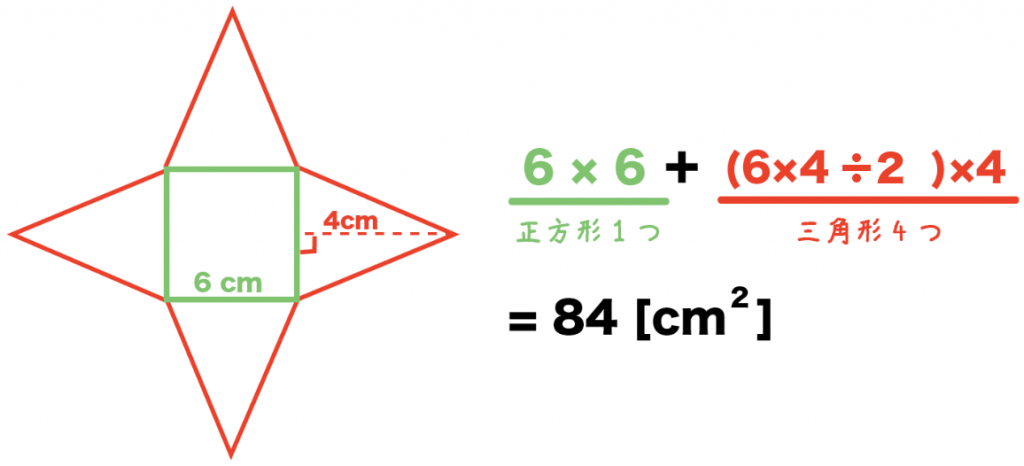
6×6 + (6×4÷2) ×4
= 84[cm²]
っていう感じで、正四角錐の表面積が計算できちゃうんだ。やったね。
最後は「正方形の1辺の長さ」と「正四角錐の高さ」がわかっているパターンだよ。
これもさっきのパターンと同じで、
「正方形の1辺の長さ」と「正四角錐の高さ」から「側面の三角形の高さ」をだしてやれば表面積を求めることができるよ。
たとえば、
底面の1辺の長さが「8cm」、高さも「8 cm」の正四角錐があったとしよう。
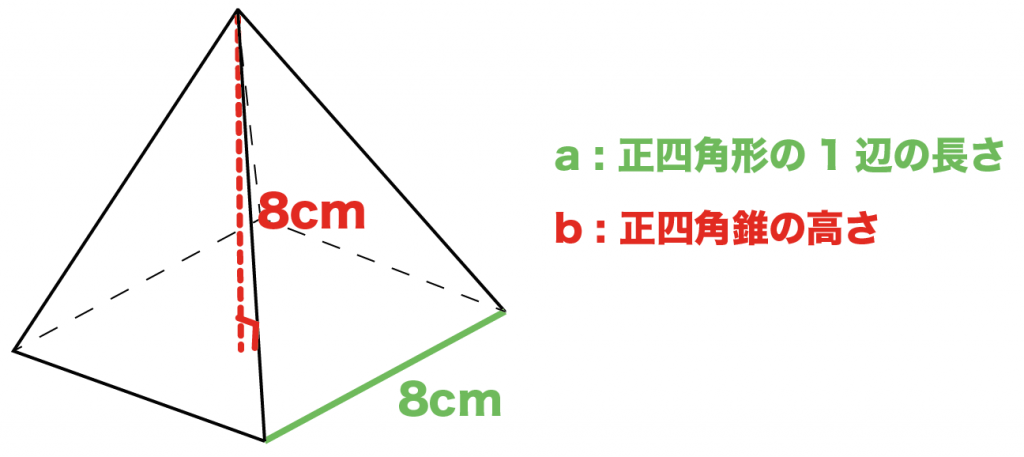
このとき、
「正四角錐の高さ」と「側面の三角形の高さ」を1辺とする三角形を考えてみよう。
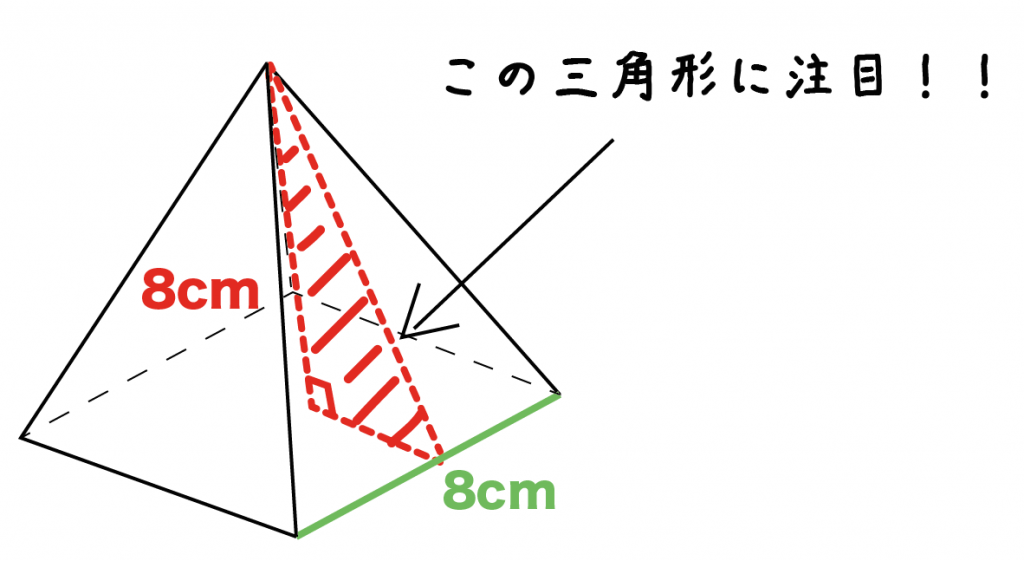
正四角錐の頂点からおろした垂線は、ちょうど底面のど真ん中に着地しているね。
だから、この三角形の底面は正方形の辺の半分の「4cm」になる。
三平方の定理をつかって、斜面の長さを求めてやると、
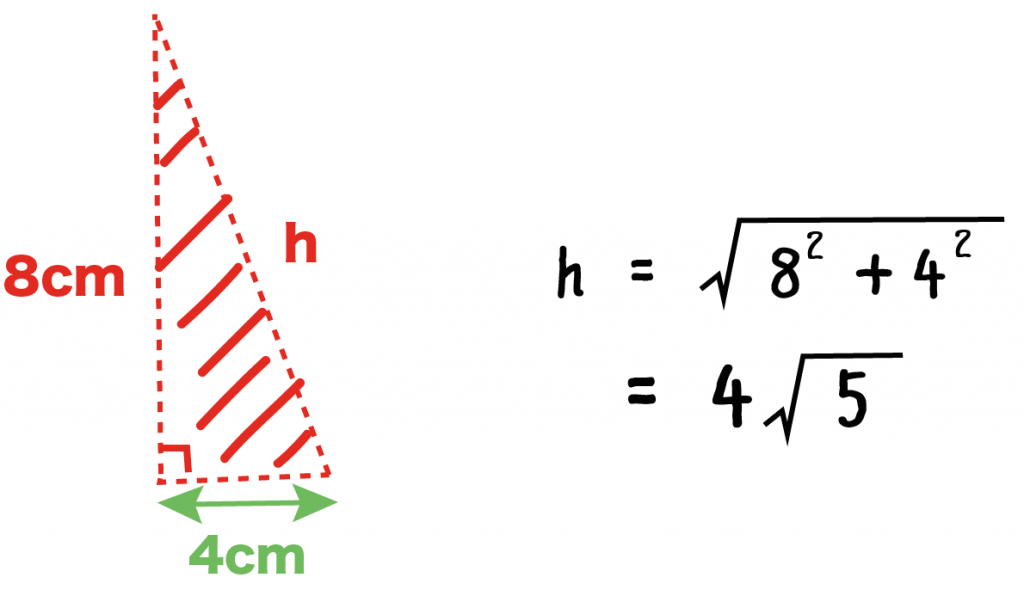
h = √(8² + 4²)
= 4√5
になる!
側面の三角形の長さがわかってしまえばあとは計算するだけ。
正四角錐の表面積は、
「底面の正方形」+「側面の三角形」×4
で求めることができるから、
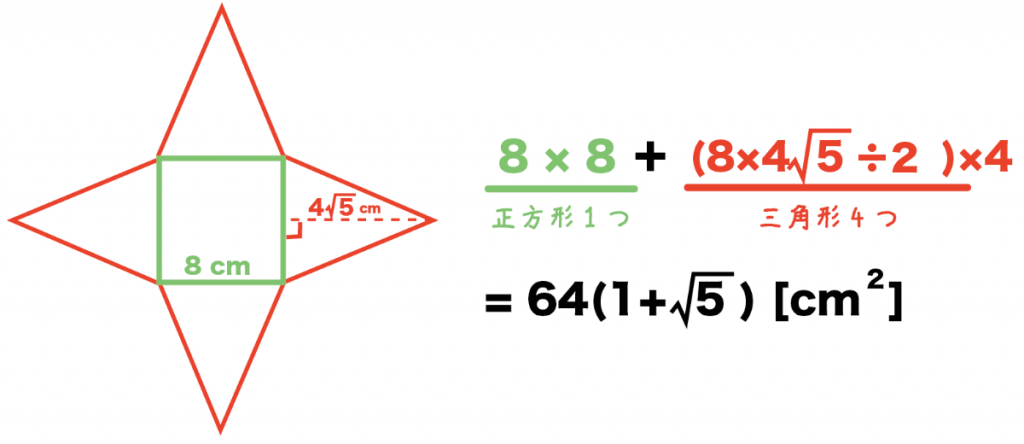
( 8 × 8 ) + (8×4√5 ÷2 ) × 4
= 64 ( 1 + √5) [cm²]
となる。
おめでとう!これで正四角錐の表面積が計算できたね。
正四角錐の表面積の求め方の問題がでたら、
自分が解こうとしている問題がどのタイプか??
ということを探ってみよう。そして、
いかにして側面の三角形の高さをだすか??
ということを考えてみよう!
そんじゃねー
Ken