【中学数学】相似の証明問題の書き方がわかる3ステップ
相似の証明問題の書き方ってあるの??
どうも、Drリードだよ。
中3数学の図形では、
図形と相似
を勉強してくよね。
この単元のなかでもやっかいなのが、
相似の証明問題
だ。
まず、証明とか苦手なのに、
図形の相似を証明しなきゃいけないときてる。
正直、きちいね。
でもね、じつは、
相似の証明問題には書き方のルールがあるんだ。
これならどんな相似の証明問題もイチコロさ。
相似の証明問題を書く前に準備する2つのこと
相似証明問題の書き方を紹介していく前に、
2つのことをやっておこう。
- 図形に印をつけろ
- 相似な三角形をさがす
つぎの相似の証明問題で練習してみようね。
つぎの2つの三角形が相似であることを証明しなさい。
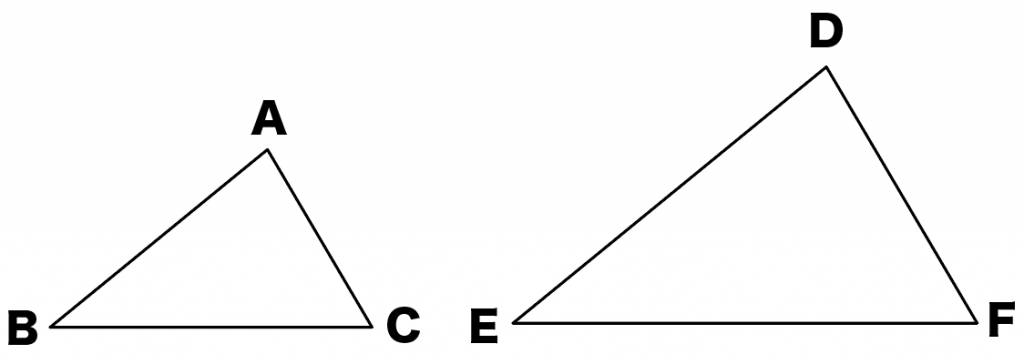
ただし、
- AB = 5 cm
- BC = 6 cm
- DE = 10 cm
- EF = 12 cm
- 角B = 角E = 30°
とします。
Step1. 図に印を書き込む
まずは、
問題でわかってる条件(仮定)
を図にかきこんでみよう。
練習問題では、
- 三角形の辺の長さ
- 三角形の角度
がわかってたよね??
さっそく書き込んでやると、こうなる↓↓
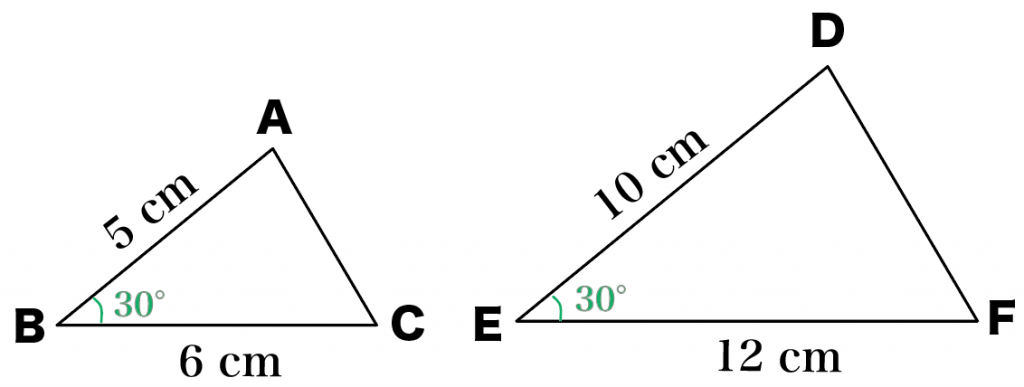
んで、
同じ角度・辺の長さ同士に、「同じ印と色」をつけてやると、
こうなるね↓↓
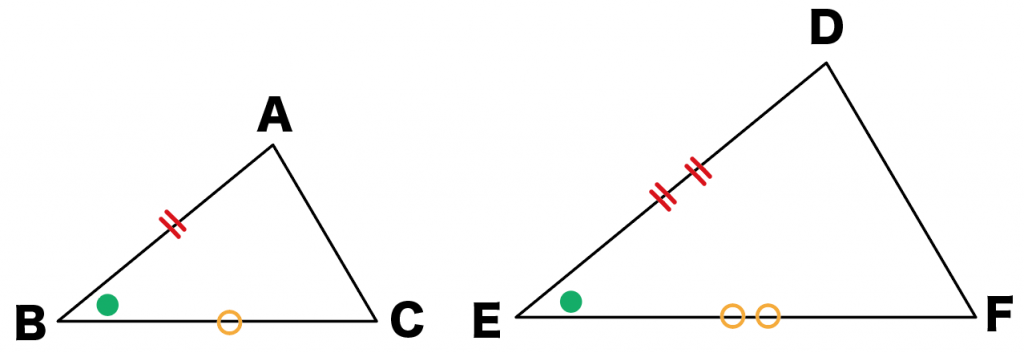
Step2. 相似な三角形をさがす
つぎは、相似な三角形をさがそう。
三角形の相似条件にあてはまる2つの三角形をさがせばいいのさ。
念のため、三角形の相似条件を確認しておくと、
- 3組の辺の比がすべて等しい
- 2組の辺の比とその間の角がそれぞれ等しい
- 2組の角がそれぞれ等しい
だったよね??
ってことで、練習問題をみてみると、
2組の辺の比とその間の角がそれぞれ等しい
がつかえそうってことに気づかない??

だって、三角形の2組の辺の比が、
- AB : DE = 5:10 = 1 :2
- BC : EF = 6 : 12 = 1 : 2
で両方1:2で等しいし、
その間にはさまってる角の、
- 角B
- 角E
が両方30°になってるからね。
えっ。簡単すぎるって??!
本番の証明問題はもっと複雑でみつけにくいよ。
まだまだ油断大敵。
相似の証明問題の書き方がわかる3ステップ
それじゃあ、相似の証明を実際にかいてみよう。
書き方はつぎの3ステップ。
- 図形を宣言
- 自分でみつけた根拠をかく
- 相似の条件と式をかく
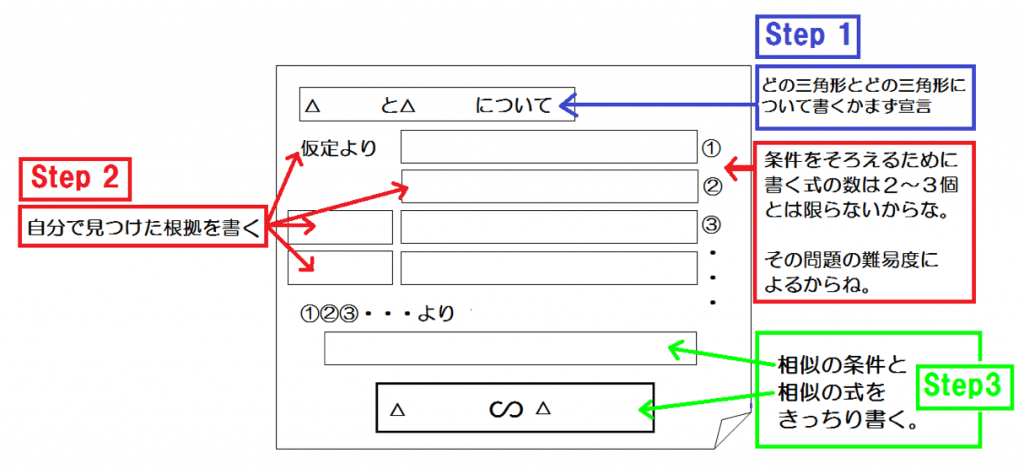
Step1. 使う図形を宣言する
まずは、どの図形で相似を証明するのかを宣言しよう。
相似の証明問題では、おもに、
準備でみつけた「相似になりそうな三角形」を宣言することが多いね。
練習問題では、
△ABC と△DEFが相似疑惑だったよね??

だから、証明のいちばん最初に、
△ABCと△DEFについて、
って宣言すればいいんだ。
Step2. 相似の根拠をかく
つぎは、
図形が相似になる根拠をかいていこう。
図や問題文からわかってることをかけばいいよ。
相似条件にあてはまる根拠をかいていけばいいのさ。
まずは、仮定からわかることを書いていこう。
問題文の中に書かれていることを数式にしてみよう。
練習問題では仮定として、
- AB : DE = 5:10 = 1 :2
- BC : EF = 6 : 12 = 1 : 2
- 角B = 角E
がわかってたよね??
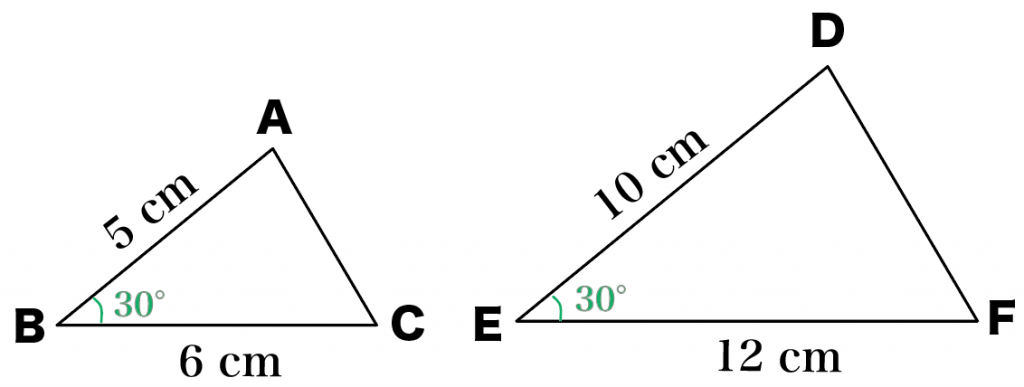
この仮定だけで相似条件でつかえそうだから、
証明の根拠はこれだけでいいんだ。
Step3. 相似条件・式をかく
相似の証明の最後では、
なぜ、相似がいえるのか??
という相似条件と、
宣言した図形が相似であること
を記号であらわしてみよう。
練習問題で言うと、
△ABCと△DEFが相似になってたね??
つかった相似条件は、準備でもみてきたように、
2組の辺の比とその間の角がそれぞれ等しい
だ。
これにより、
△ABC ∽ △DEF
がいえるってかけばいい。
これで相似の証明はおわり!
実際に相似の証明をかいてみよう!
それじゃあ、この書き方で相似の証明をかいてみよう。
こんなかんじになるよ↓
△ABCと△DEFについて
仮定より、
AB:DE = 5:10 = 1:2 ・・・①
BC:EF = 6:12 = 1:2 ・・・②
∠ABC = ∠DEF ・・・③
①②③より、
2組の辺の比とその間の角がそれぞれ等しいので、
△ABC ∽ △DEF
まとめ:相似の証明問題の書き方は使いまくっておぼえろ!
最後にもう一度復習しておこう。
相似の証明問題を書く前の準備は、
- 図形に印をつける
- 相似な三角形をさがす
だったね。
んで、相似証明問題の書き方は、
- 図形を宣言
- 相似の根拠をかく
- 相似条件、相似の式をかく
の3ステップ。
これで何とか道は開けるよ。

何がわかっていて、あと何がわかれば、
相似の条件がそろうのか考えてみよう。
証明を書き始める前にしっかり用意してね。
次は「相似の証明問題でマスターしておきたい3つのパターン」について話す予定だよ。
相似の証明を極めたいやつは読んでみてくれ。
それじゃあ
Drリード



