【中3数学】中点連結定理の証明がわかる3ステップ
中点連結定理の証明ってどうやるの??
どーも、ぺーたーだよ。
図形と相似の単元で、
中点連結定理
を勉強していくよね。
えっ、忘れたって!?
中点連結定理を簡単にいってやると、
三角形の2辺の中点を通る線が、
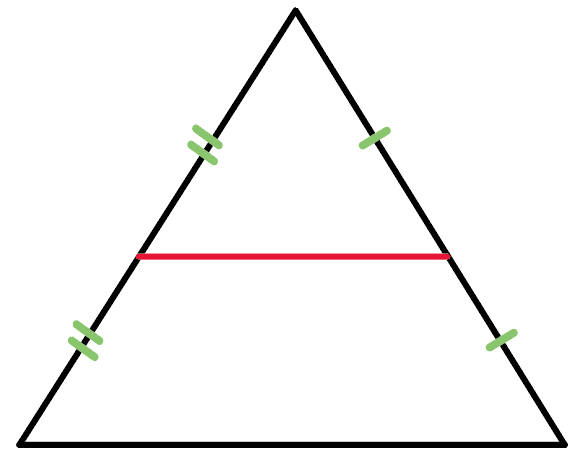
底辺に平行で、
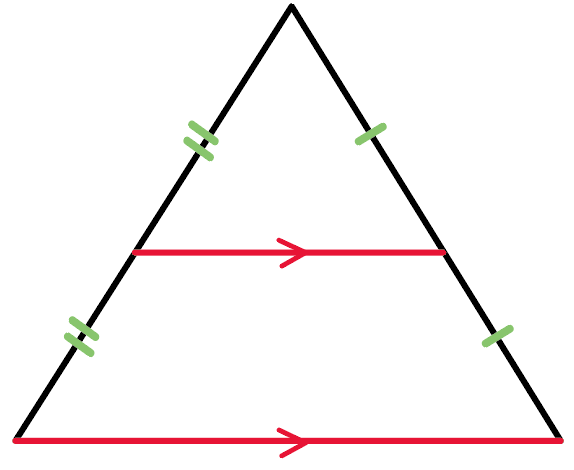
なおかつ、
底辺の半分になってるよー
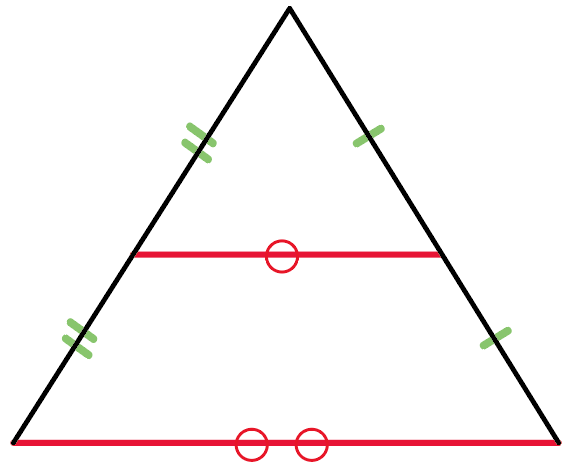
っていう定理なんだ。
けっこう便利なんだけど、
なんでそうなるの?
って思ったことはないかな?
思ったことがなくても、
中点連結定理を使えれば大丈夫なんだけどねw
ってことで、今日は、
なんで中点連結定理が使えるか??
を証明していくよ!
中点連結定理の証明がわかる3ステップ
さっそく中点連結定理を証明していくよ。
3ステップで証明できちゃうんだ。
- 相似の証明
- 相似比を求める
- 平行の証明
中点連結定理を証明するために、
つぎの、
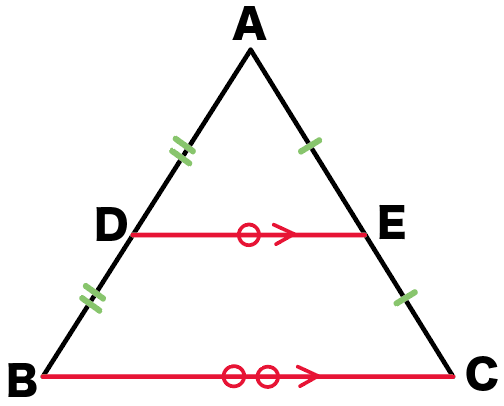
△ADEと△ABC
を思い浮かべてみて。
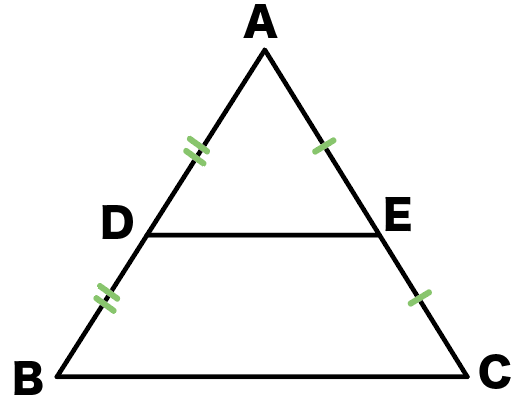
DとEはそれぞれ、ABとACの中点ね。
中点連結定理の証明のゴールは、
- DE = 1/2 BC
- DE//BC
を証明することだよ。
さっそく証明していこう!
Step1. 相似の証明
まずは△ADEと△ABCの相似の証明だ。
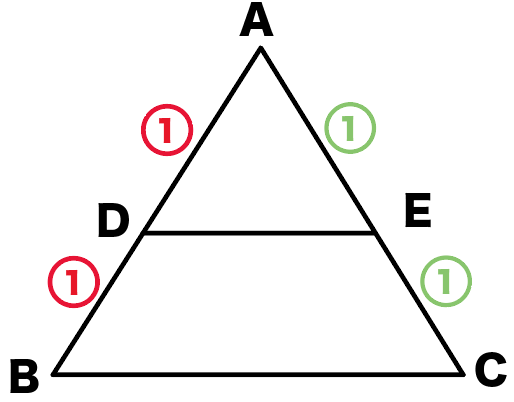
D・Eはそれぞれの中点だから、
- AD=DB
- AE = EC
だよね??

ってことは、比であらわすと、
- AD:DB=1:1
- AE:EC=1:1
になるはずなんだ。
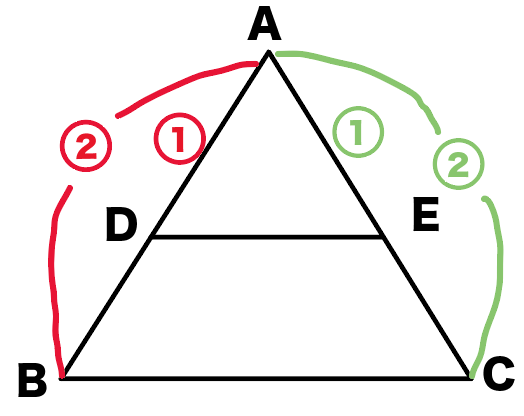
ADとDBの比を合わせると、
AD:AB=1:2…①
ACの比も同じ考え方でAEとECの比を合わせると、
AE:AC=1:2…②
になるね。
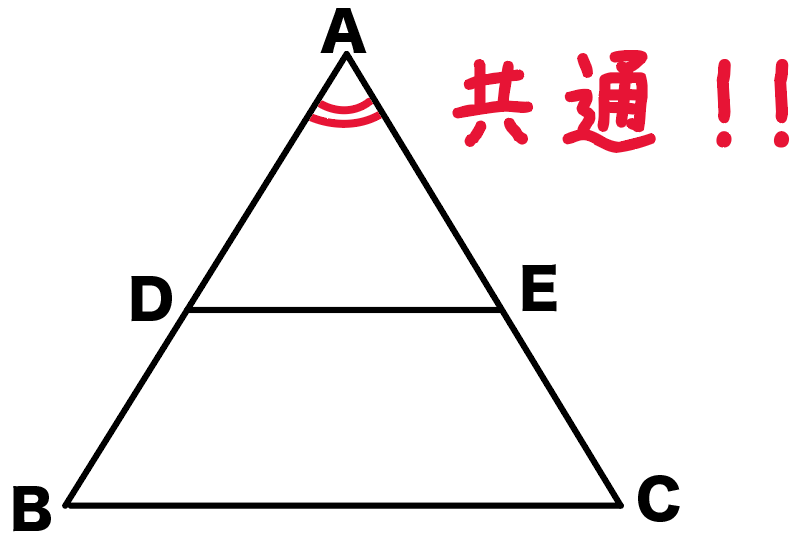
んで、
△ADEと△ABCは角Aを共有してるよね??
ってことで、
角DAE = 角BAC (共通)…③
だ。
①、②、③より、三角形の相似条件の、
2組の辺の比とその間の角がそれぞれ等しいが使えるから、
△ADE∽△ABC
になるね。
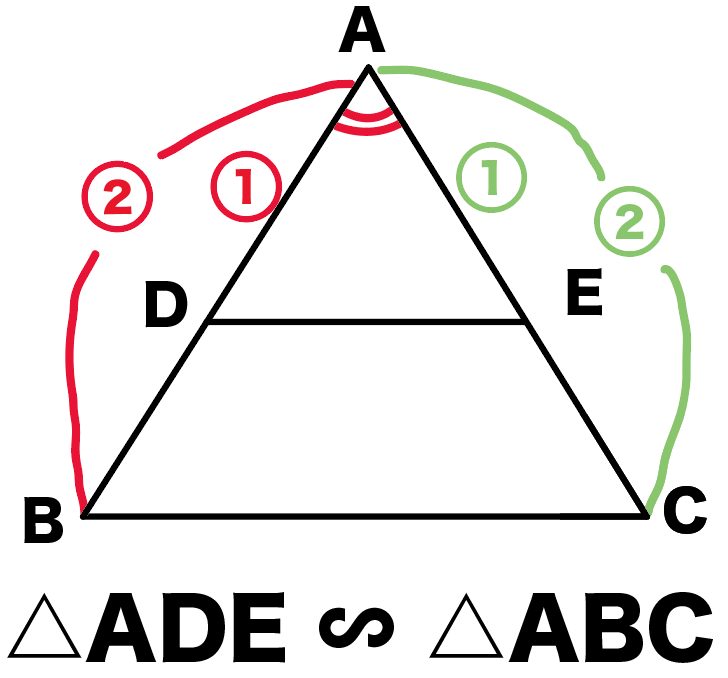
これで相似の証明はできた!
Step2. 相似比を求める
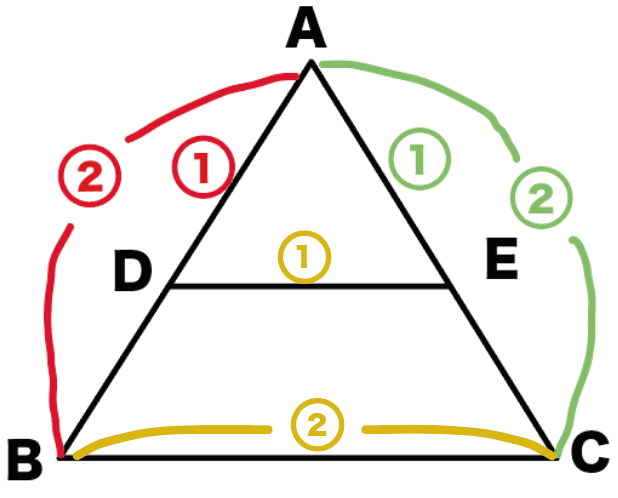
三角形の相似比を求めてみよう。
①のAD:AB=1:2より、
△ADEと△ABCの相似比は1:2になるよ。
なぜなら、
ADとABは対応してる辺どうしだからね。

つまり、
△ADEと△ABCの対応する辺の比は全て、
1:2になるはずなんだ。
ってことは、残りの対応する辺の、
DEとBCの相似比も1:2になるね。
DE:BC=1:2
こいつを別の言い方をすると、
DE=1/2BC
ともできるよね。
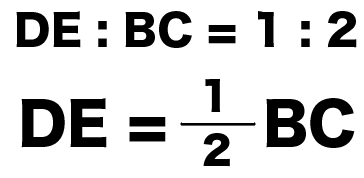
これでDEがBCの半分になるってことはわかったね!
Step3. 平行の証明
あとは、
DEとBCが平行であること
を証明していこう。
これで中点連結定理の証明が完了するね。
平行の証明には、
同位角が等しいこと
をつかっていくよ。
△ADE∽△ABCだから、相似の図形の性質をつかうと、
対応する角はすべて等しいはずだね。
ってことは、
角ADE = 角ABC
がいえちゃうんだ。
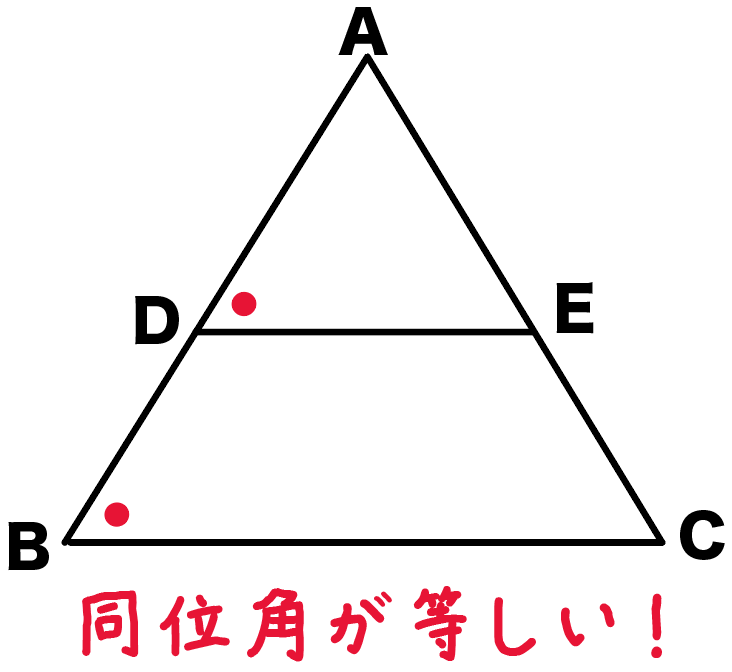
こいつらは、どうみても同位角。
同位角が等しいから、
同位角をつくってるDEとBCは平行
ってことがいえるんだ。
ってことで、
DE // BC
になるよ。
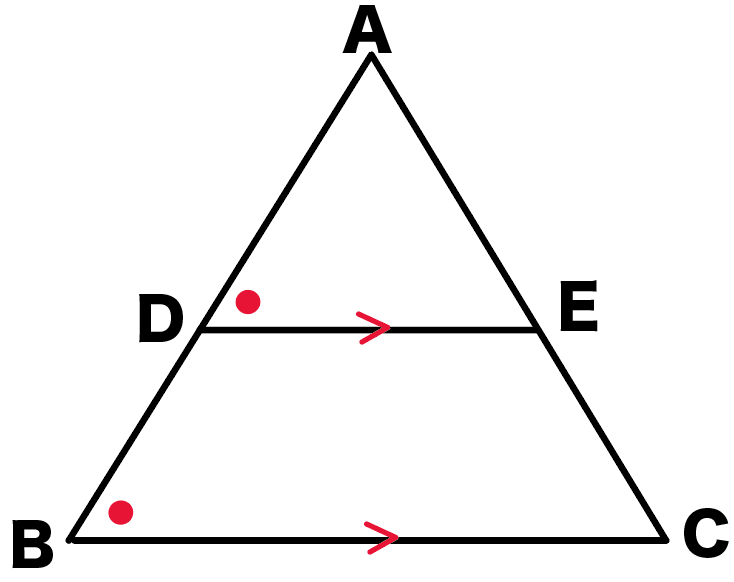
ここまでの3つのステップから、
DE//BC
DE=1/2BC
であることが言えるんだ。

おめでとう!
中点連結定理を証明できたね!!
まとめ:中点連結定理の証明はステップ踏めばOK
ここまでで、中点連結定理は証明できたね??
べつに証明はできなくてもいいけど、
なぜ、中点連結定理がつかえるのか??
ということは、ふんわりでもいいから頭の片隅においておいてね。
じゃ、またね!
ぺーたー


