一次関数と二次関数の交点の求め方がわかる3つのステップ
一次関数と二次関数の交点を求める問題??
こんにちは!この記事をかいてるKenだよ。シロップはやさしいね。
中学数学では二次関数y=ax2を勉強するよね??
二次関数の問題にはたくさんあって、
放物線のグラフをかいたりしていくよ。
なかでも、テストにでやすいのは、
一次関数と二次関数の交点を求める問題
だ。
こんなふうに、
一次関数と二次関数y=ax2が交わっていて、
その交点を求めてね?
って問題なんだ。
今日はこの問題の解き方をわかりやすく解説していくよ。
よかったら参考にしてみて。
一次関数と二次関数の交点の求め方がわかる4ステップ
さっそく交点をもとめてみよう。
たとえば、つぎの練習問題だね。
—————————————————————————–
練習問題
二次関数 y=x^2 と一次関数 y=x+6 の交点を求めてください。
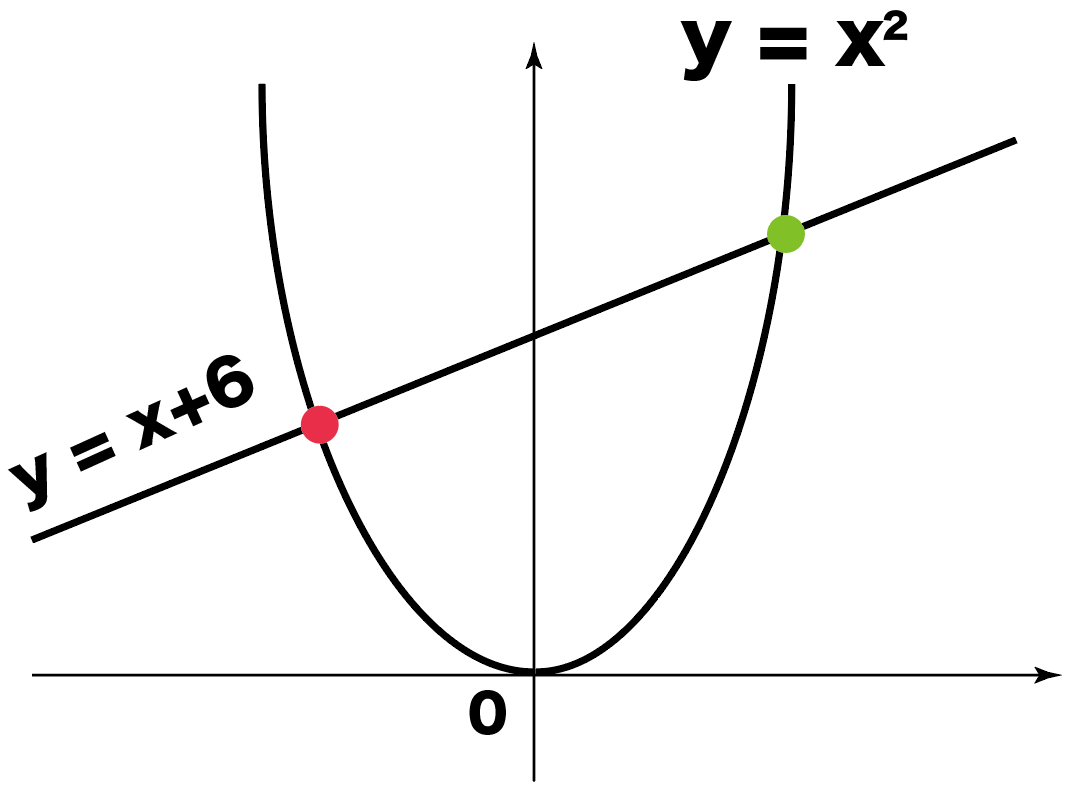
Step1. 連立方程式をつくる
関数の交点を求めるには、
連立方程式をつくるのが一番。
一次関数のときにならった、
2直線の交点の求め方とやり方はおなじだね。
練習問題でも連立方程式をつくってみると、
- y=x2
- y=x+6
こうなるね。
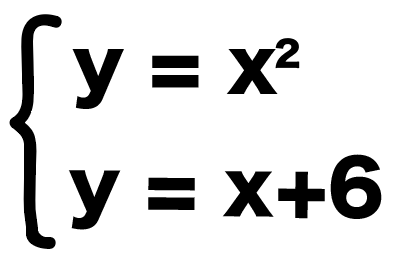
この2つの方程式から、xとyの値を求めていけばいいのさ。
Step2. 連立方程式をとく
さっそく連立方程式をといていこう。
連立方程式の解き方は、
の2つあったよね??
関数の交点を求めるときは、
代入法をつかっていくよ。
なぜなら、
「y =○○」になっていてyが代入しやすいからね。
Step3. 二次方程式をとく
つぎは二次方程式をといていこう。
二次方程式の解き方はたくさんあるけど、
どれをつかっても大丈夫。
練習問題の、
x^2 = x + 6
も解き方はいっしょ。
左辺にぜんぶの項を移項してみると、
x^2 – x – 6 = 0
になるね。
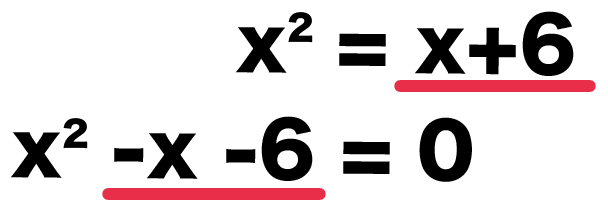
こいつを因数分解すると、
x^2 – x – 6 = 0
(x – 3) (x +2) = 0
になる。
あとは、どっちかが0になっていれば式がなりたつから、
- x – 3 = 0
- x + 2 = 0
この一次方程式をといてやると、
- x = 3
- x = -2
になるね。
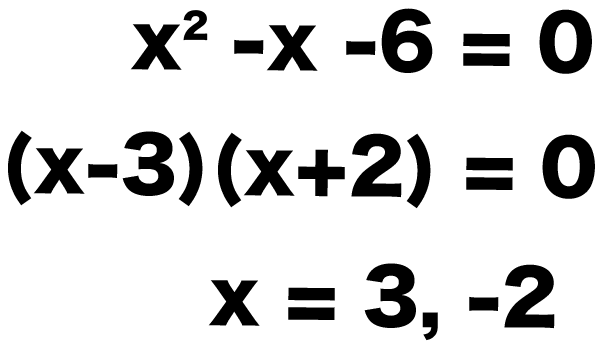
Step4. xを関数に代入
最後にxを関数に代入してみよう。
関数にxをいれるとy座標がわかるからね。
2つの交点のx座標が、
- 3
- -2
ってわかったよね??
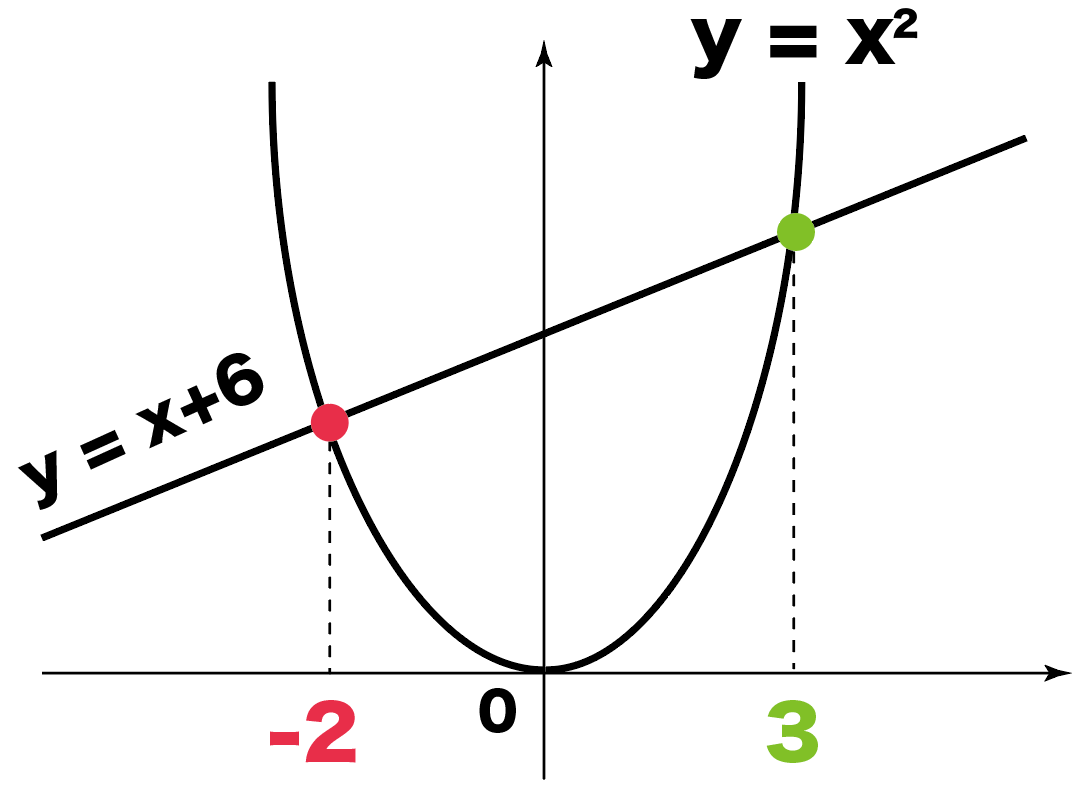
このx座標を、
「二次関数」か「一次関数」
のどっちかに代入するんだ。
今回は、そうだな、
簡単な一次関数「y=x+6」に代入してみよう。
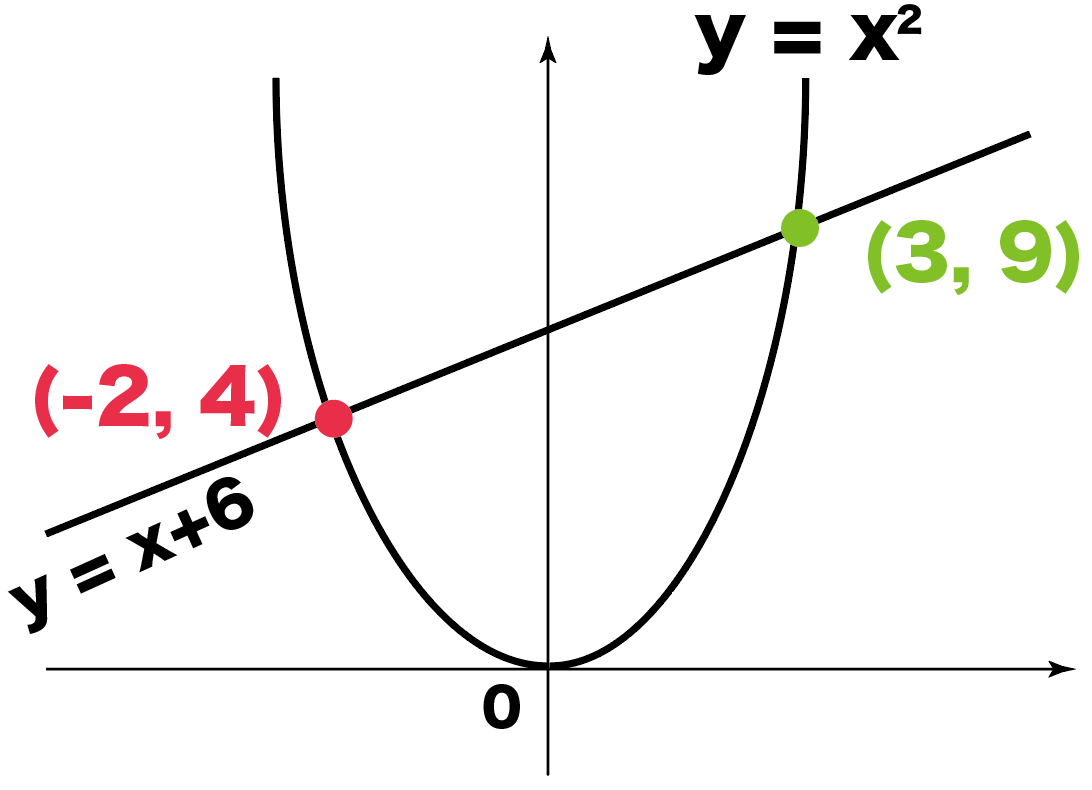
すると、2つの交点のy座標は、
- x = -2のとき、 y = -2 + 6 = 4
- x = 3のとき、y = 3 + 6 = 9
になる。
よって、2つの交点の座標は、
- (-2, 4)
- (3, 9)
の2点になるね。
おめでとう!
これで一次関数と二次関数の交点が求められたね。
まとめ:一次関数と二次関数の交点もどんとこい!
一次関数と二次関数の交点を求める問題はよくでてくるよ。
なぜなら、中学数学の総復習になるからね。
テスト前によーく復習しておこうね。
そんじゃねー
Ken


