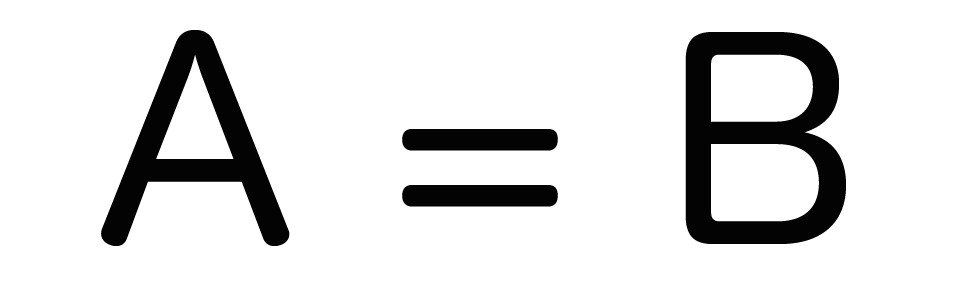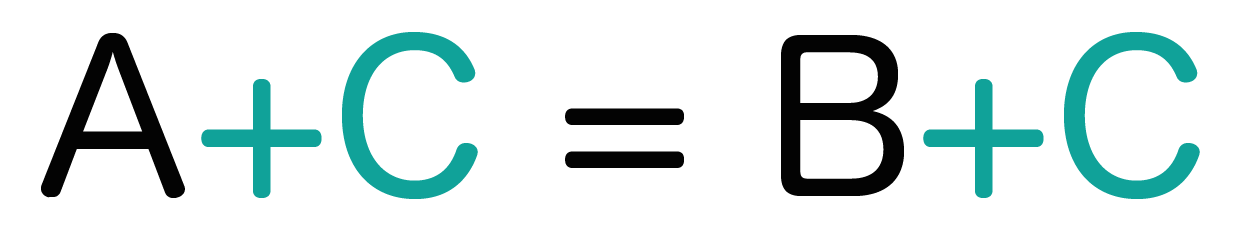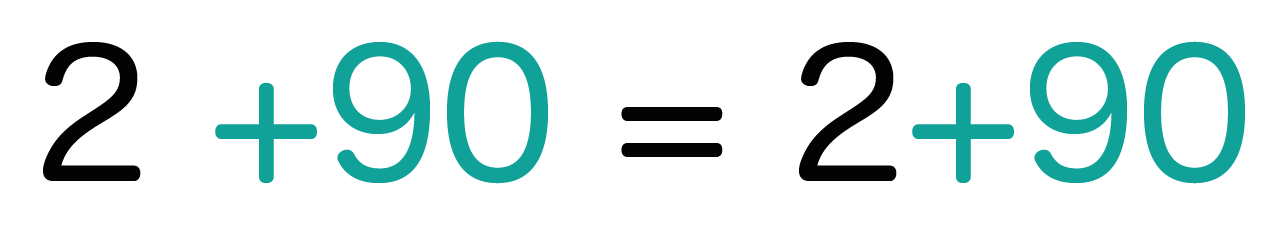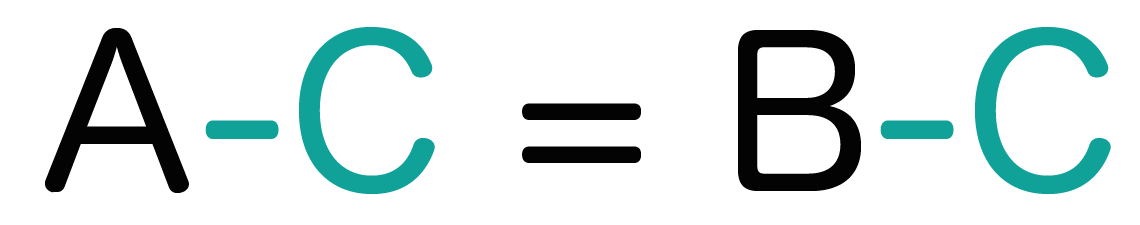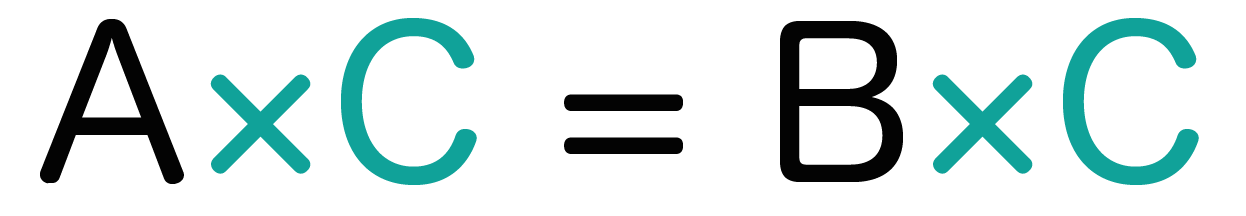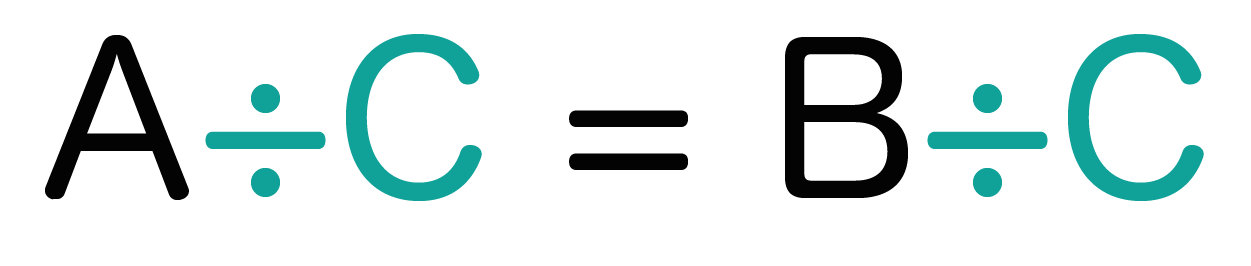方程式を解くのに便利!4つの等式の性質
方程式を解くのに必要な「等式の性質」って!??
こんちゃ!ストーブでやけどしそうになったKenだよ。
中学1年数学の山場は「方程式」。ここさえ超えてしまえばあとは楽勝なんだ。ちょっと難しそうに聞こえても辛抱強く粘ってみよう!

そんで、
前回まで「方程式を解く」ということを勉強してきたけれど、
じつは方程式を解くためにはたった1つのことを利用してやればいいんだ。
それは、
等式の性質
というやつさ。言葉を言い換えれば、
等式にはどんな特徴があるのか???
という話。これさえ理解してしまえば方程式を解くなんてちょちょいのチョイ。中学数学で勉強する「等式の性質」というものはぜんぶで4つあるんだ。
今日はめんどくさいし、せっかくだから等式の性質というものをすべて復習してみよう!
方程式につかえる4つの「等式の性質」
中学の数学で勉強する「等式の性質」とやらは次の4つだ。ちょっと等式というものがよくわからん、というときは等式についての記事の、
っていう2つの記事を参考にしてみてね。きっとピンとくるはずだ。うん。
それじゃあさっそく、等式の性質をみていこう!
等式の性質1. 「左と右に同じものを足してもOK!!」
1つ目の等式の性質は、
「左の式」と「右の式」に同じ数字を足しても等式は成り立つ!
ということ。ちょっと言葉だけじゃわかりにくいから例題をみてみよう。
たとえば超シンプルな「A = B」という計算式があったとする。
前にも習ったけど、
これは左のAと右のBの値が等しい
ということを表してるね?? そんで、この左右両方にCという数字を足してあげよう。
すると、次のようになる。
同じ数字「C」を左と右の両方に足しても、まだ成り立っているということが言えるんだ。
つまり、
A + C
と、
B + C
の値が等しいということ。これはちょっと理科でならった「てんびん」に似ているね!
てんびんの左右に同じ重さのおもりをのせても釣り合ったよね?? 等式はチョー「てんびん」に似てるんだ。等式の意味を忘れそうになったら理科のてんびんを思い出してみよう!
等式の性質を確認するためにAとかBとかCとか胡散臭い文字を使ったけど、実際の数字を使ったって大丈夫。たとえば、
2 = 2 という等式の、
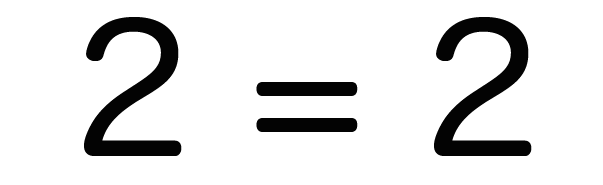
左右両方に「90」という大きな数字を足してみてもいい。
左にも右にも同じことしてやれば等式は保たれるんだ。これから紹介する残り3つの等式の性質もやってることはだいたい一緒だよ。
等式の性質2. 「左と右の両方から同じ数字をひいてもOK!!」
等式の2つ目の性質は、
「左と右の両方から同じ数字をひいても等式は成り立つよ」
というもの。1つ目の「等式の性質」の足し算を引き算に変えただけだね。
これもさっきと同じ等式の「A = B」を使って考えてみよう。
この左と右の両方から「C」という数字をひいてあげるんだ。
そうすると、
こうなるね。
同じ数字をひいても等式は成り立つってこと! 1つ目の性質とあまり変わらないね。
等式の性質3. 「左と右に同じ数字をかけてもOK!!」
この等式の性質もだいたい一緒だ 。
等式の左右両方に「同じ数字」をかけても等式は成り立つってこと!
たとえばさっきの「A = B」という等式に、
Cという数字を左と右の両方にかけてあげる。
すると、こうなるね。
これが3つ目の等式の性質。1つ目と2つ目とだいたい一緒だね!。
等式の性質4. 「左と右の式を同じ数で割ってもOK!!」
もうそろそろ飽きてきたと思うけど、次で最後の「等式の性質」だ。
左と右の両方の式を同じ数で割っても等式は成り立つよ!
っていうのが等式の最後の性質。
さっきと同じように「A = B」という等式があったとすると、
同じ数「C」で左と右の両方の式を割ってあげればいいんだ。
こんなことをしても等式はまだ成り立つということ。こいつもこれまでの等式の性質とだいたい一緒だね。
まとめ:等式の性質とは「左と右に同じことしても大丈夫」
さあ、ここまで4つの等式の性質をみてきたね。
だいたいどれも似ていたけど、つまり簡単にまとめてしまえば次のような性質になるんだ。
等式の左と右に同じ数字を足しても、ひいても、かけても、割ってもいい
ということ。
つまり、等式の左と右の計算式に同時に同じ数字を四則演算しても等式は成り立つ。
これを覚えていれば問題ないよ。
いかにも当たり前のことを言っているけれど、
これがのちのち方程式の解き方に効いてくるからしっかりと押さえておこうね。
それじゃねー!!
Ken