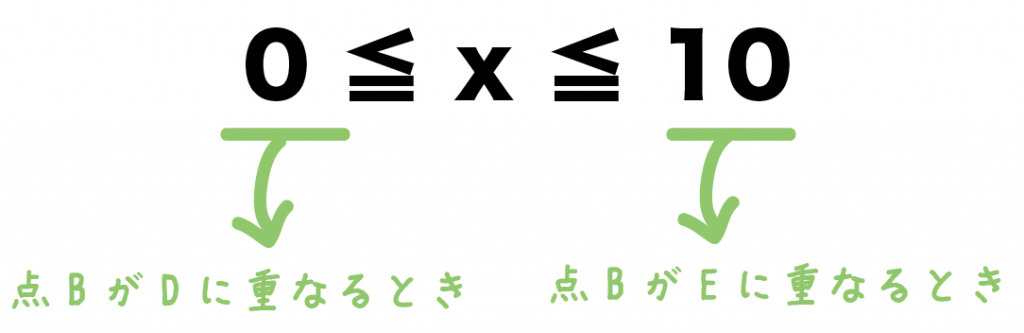【二次関数の利用】図形の文章問題の解き方がわかる3ステップ
二次関数の利用の図形の問題の解き方がわからん!
こんにちは!この記事をかいてるKenだよ。徒歩はこころにいいね。
中学数学で二次関数をたくさん勉強してきた。
グラフの書き方とか、
比例定数の求め方とか、
変域の問題とか、
ほんといろいろ。
今日は最後のとりでの、
二次関数の利用を勉強していこう。
とくにテストにでやすい、
図形を移動させる文章問題
をいっしょにといていこうね。
二次関数の利用の図形の文章問題がわかる3ステップ
さっそく問題をといてみよう。
練習問題
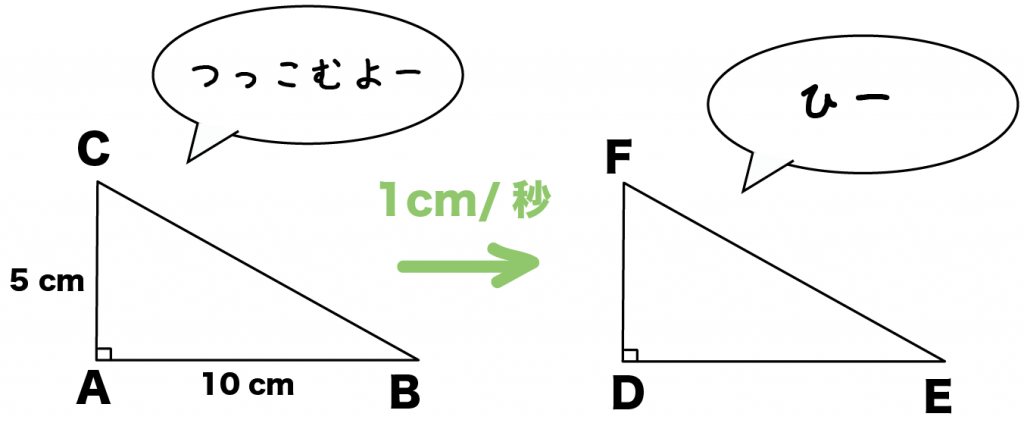
1辺の長さが5cm、10cmの直角三角形ABCがあります。
こいつと合同な直角三角形DEFがちょっと先においてあります。
△ABCを毎秒1cmの速さで△DEFにむかって動かします。
点BがDからEまで動くとプログラムされてます。
点Bが点Dにきてからx秒後の三角形が重なった部分の面積をy[cm^2]とするとき、
yをxの式であらわしてください。
あと、グラフとxの変域とかも答えてくれ。
つぎの3ステップで解けちゃうよ。
Step1. 重なる部分をイメージする
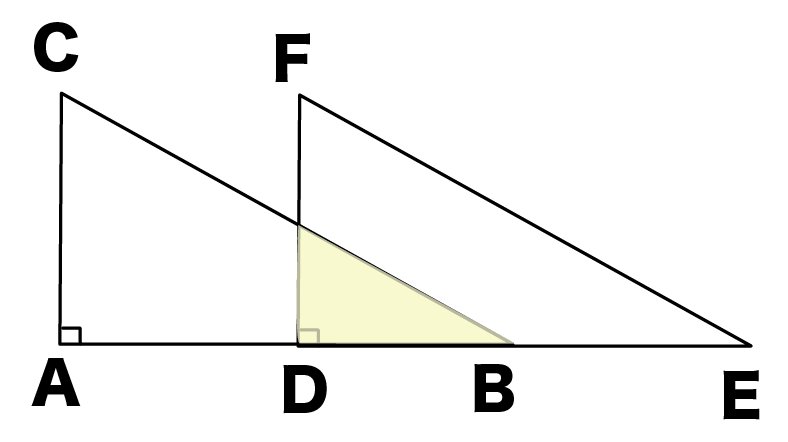
三角形が重なる部分をイメージしよう。
この面積がyになるはず。
想像できないと関数の式つくれないよね?
実際にイメージしてみるために、
2つの三角形をぐいっと近づけてみよう。
すると、2つの三角形が重なる黄色い部分ができるじゃん??
イメージできれば第1ステップ終了。
Step2. 底辺をだす
三角形の面積は、
底辺×高さ÷2
だったよね??
ってことは、重なった三角形の面積をだすには、
- 底辺
- 高さ
の2つが必要になるわけ。
ってことで、まずは底辺。
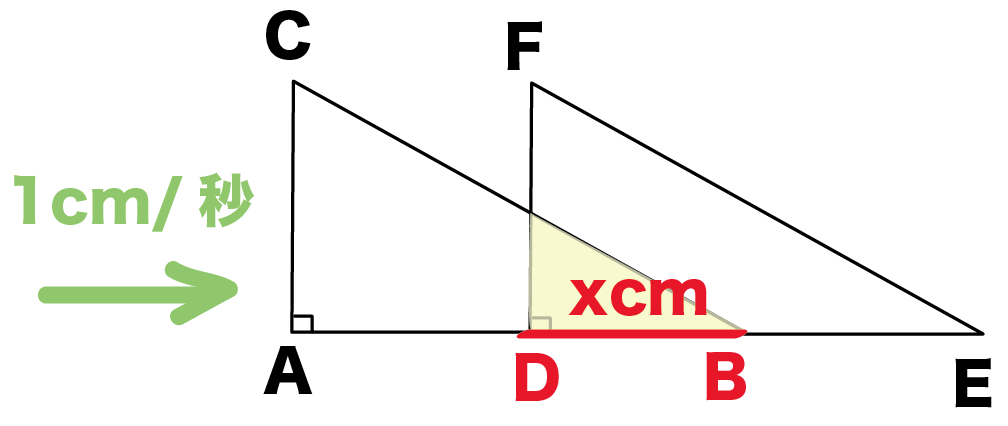
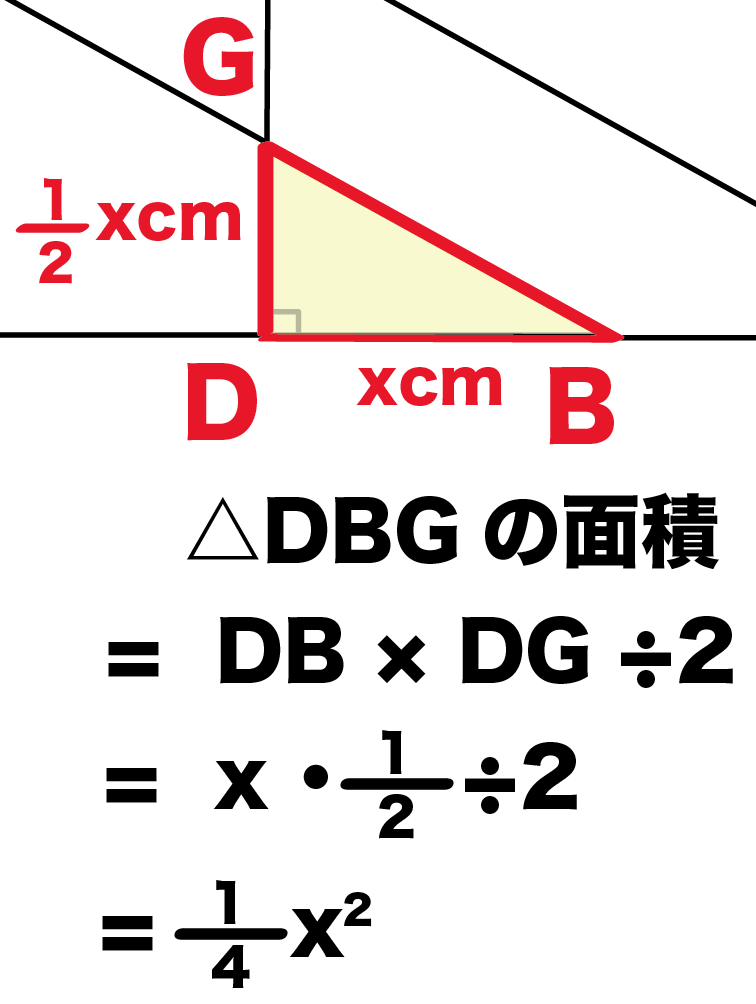
練習問題の辺DBの長さを求めればいいんだね。
BがDにきてからx秒後のね。
点BがDにきたときのDBの長さは0だ。
ここから、1秒間に1cmの速さで三角形は右に動いていくから、
x秒後には、
DB = x cm
になってるはず。
Step2. 高さをだす
つぎは三角形の高さをだしてみよう。
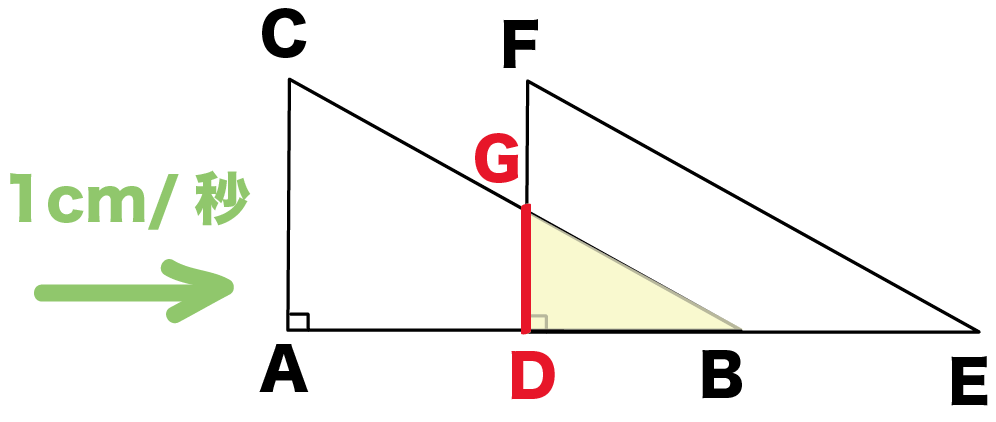
BCとDFの交点をGとすると、2つの三角形が重なってできる三角形の高さは、
DG
だよね??
この辺の長さは、
△ABCと△DBGが相似ってことをつかえば求められる。
なぜ、こいつらが相似な関係にあるのかというと、
- 角ABC = 角DBG
- 角CAB = 角GDB = 90
っていうかんじで、
2つの角がそれぞれ等しい
っていう相似条件をみたしてるからなんだ。
AB:AC = 2:1でなおかつ、
△ABCと△DBGは相似だね。
よって、
AB:AC
= DB: DG = 2: 1
x : DG = 2:1
DG = 1/2 x
になるね。
Step3. 三角形の面積を計算する
三角形の「底辺」と「高さ」が求められたね。
あとは、
三角形の面積を計算するだけ。
重なった部分の三角形、つまり、
△DBGの面積は、
底辺×高さ÷2
= DB ×DG÷2
= x × 1/2 x ÷2
= 1/4 x^2
になるね。
重なった三角形の面積がyだったから、
y = 1/4 x^2
になるわけね。
せっかくだからグラフと変域も求めようか。
重なった部分の面積ゲットーーー!おわたーーーー!
ってなるのははやい。
まだ、1つだけやることが残ってるんだ。
それは、
グラフをかくこと
だ。
xの変域を求めてみる
まずは、
xの変域を求めてみよう。
今回の問題では、BがDに重なってからの秒数をxとしてたね??
ってことは、
xは負の数はありえない。
つまり、
x ≧ 0
だよね??
んで、BはEまでしか進めないことになってるから、
x ≦ 10
なはず。
よって、xの変域は、
0≦x≦10
になるね。
二次関数のグラフをかいてみる
xの変域をもとにグラフかいてみようか。
x・y座標が整数になる点
をうてばいいね。
二次関数のグラフの書き方がわからんときは復習してね。
二次関数のグラフのかきかたの基本は、
座標をうちまくって雰囲気で放物線をかく
だったね???
1メモリが1の座標に点をうちこんでやるんなら、
- (6, 9)
- (4, 4)
- (2, 1)
- (0, 0)
の4点でいい。
この点をうって、それっぽい放物線をかいてやると、
こうなるはず↓↓
xが0より小さい場合は点をうったり線をかいたりしちゃダメだよ。
これで文章問題の問いにすべて答えることができたね。
おめでとう!
まとめ:二次関数の利用の図形の文章問題は変域が大事
二次関数の利用の図形の問題はどうだったかな??
図形の公式通りに等式をたてればいいんだ。
あとはxの変域を間違えないようにね。
そんじゃねー
Ken