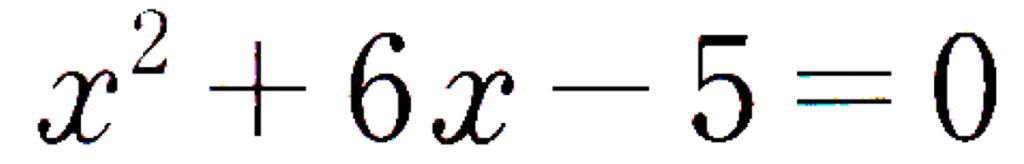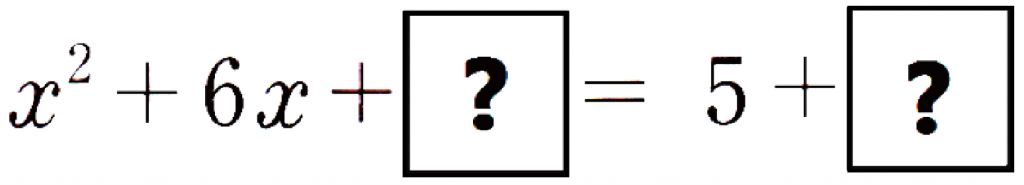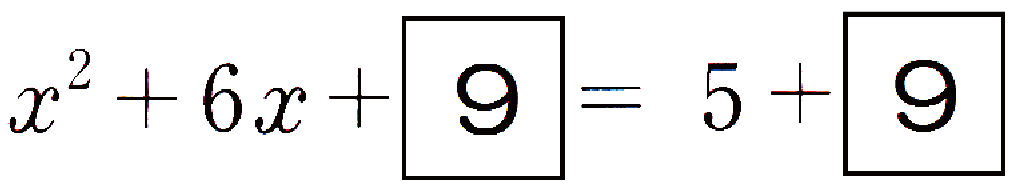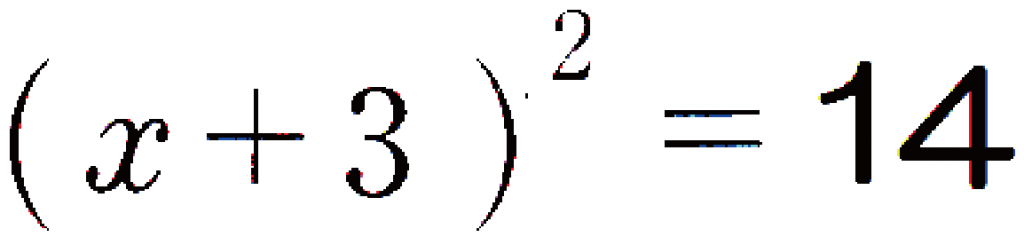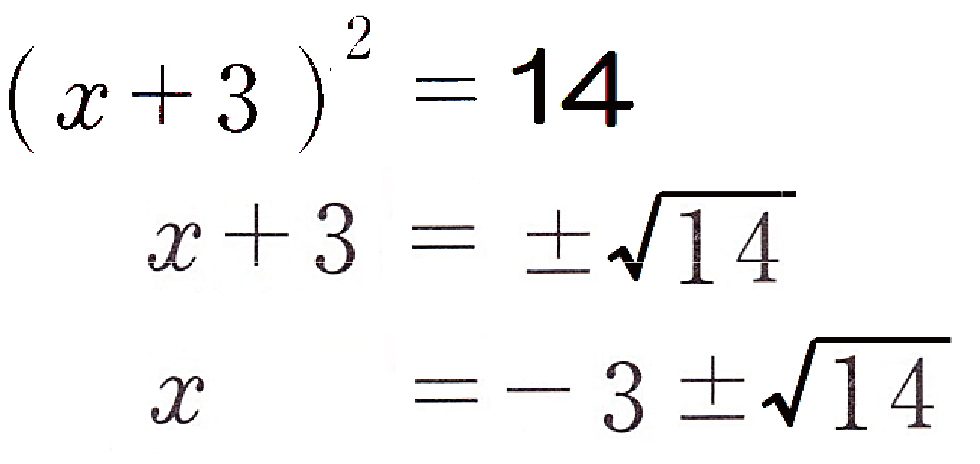平方根の二次方程式の解き方ってどうやるの？？
こんにちは！Drリードだよ。
二次方程式の解き方にはたくさん種類があったね。
今日はもう1つ解き方を勉強していくよ。
その名も、
平方完成をつかった二次方程式の解き方
だ。
この解き方は、
因数分解できなくて、
なおかつ、
解の公式を忘れたときに使える解き方なんだよ。
絶望的な状況をすくってくれるのが平方完成ってわけ。
平方完成による二次方程式の解き方3ステップ
つぎの2次方程式の問題をといていこうか。
平方完成をつかった二次方程式になれるためにね。
練習問題
つぎの二次方程式を解きなさい。
x^2 + 6x -5 = 0
Step1. 数字を右に移項する
xがついてない項を右に移項しちゃおう。
つまり、
数字の項を右によせちまえばいいわけ。
練習問題でいうと、
3つめの項の、
-5
がxがついてない項だ。
こいつを右に移項すると、
x^2 + 6x -5 = 0
x^2 + 6x = 5
になるね。
Step2. 左辺を（xをふくむ式）の2乗にする
つぎは、どんな手をつかってもいいから、
左辺を「xをふくむ式」の2乗にしてみよう。
例題の式をみてみて。
x^2 + 6x = 5
左をxをふくむ式の2乗にするために、
両辺に同じ数をたしてみよう。
左側が （ ）2 の形になるためには、「?」に何が入ったらいいと思う？
そう。
そうだよ、そうなんだ。
?には「9」がはいって、
x^2 + 6x + 9 = 5 + 9
になればいいね。
なぜなら、
左辺で因数分解の平方の公式の、
（a+b）^2 = a^2 + 2ab +b^2
がつかえるようになるからね。
さっそく因数分解してやると、
x^2 + 6x + 9 = 5 + 9
(x+3)^2 = 14
こんなかんじで、左辺に（xをふくむ式）の2乗をつくりたいときは、
xの係数の半分を2乗したやつを両辺にたせばいいね。
なっとくだ！
Step3. 平方根の解き方をつかう
ここまできたら、平方根の解き方の形になったね。
左辺の2乗をとっぱらって、右辺を左辺の平方根にすればいい。
練習問題の、
(x+3)^2 = 14
もおなじように平方根の解き方をつかってみると、
x + 3 = ±√14
x = -3 ± √14
になるね。
おめでとう！
これで平方完成の解き方もマスターだ。
まとめ：平方完成をつかった二次方程式の解き方は本当の最終兵器
このめんどくさい解き方を、
平方完成で解く方法
っていうんだ。
因数分解できなくて、解の公式も忘れたら平方完成で解く
って、覚えといてくれよ。
心配なときは、つぎの練習問題もといてみてね。
レベルの高い解き方なんだから、練習あるのみだよ。
何回もね。へいへいほ～～♪
練習問題2. つぎの二次方程式を解きなさい。
x^2 + 3x + 1 = 0
⇒ 平方完成の二次方程式の問題の答えはこちら
平方完成は高校数学ですごく大切になるんだ。
平方完成を制するものは高校数学を制すといっても過言じゃあない。
いまのうちからマスターしておこう。
そいじゃねー
Dr.リード
