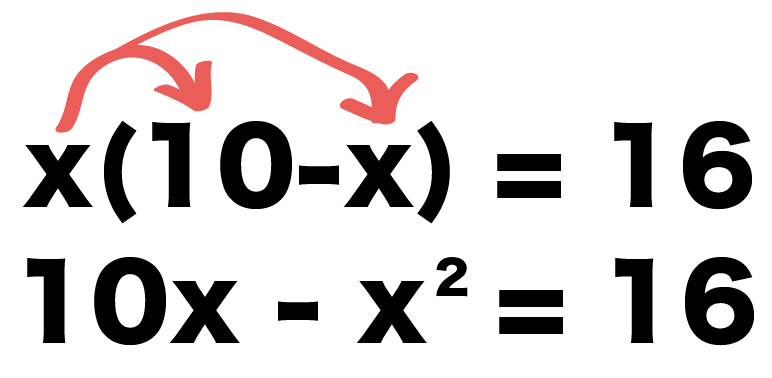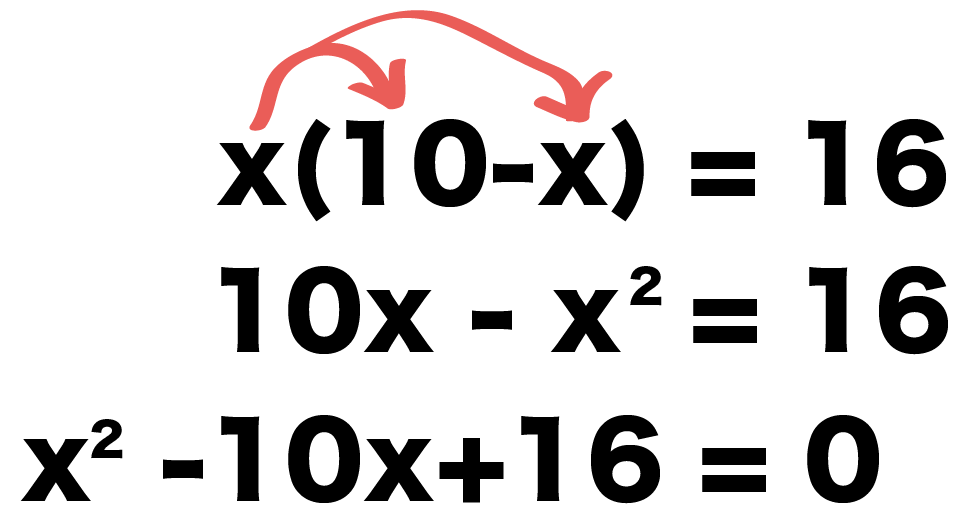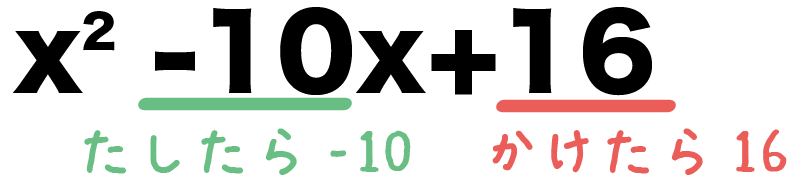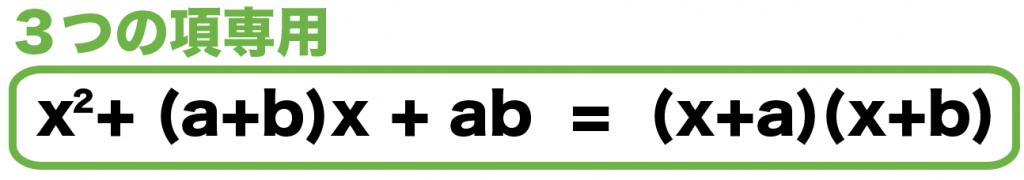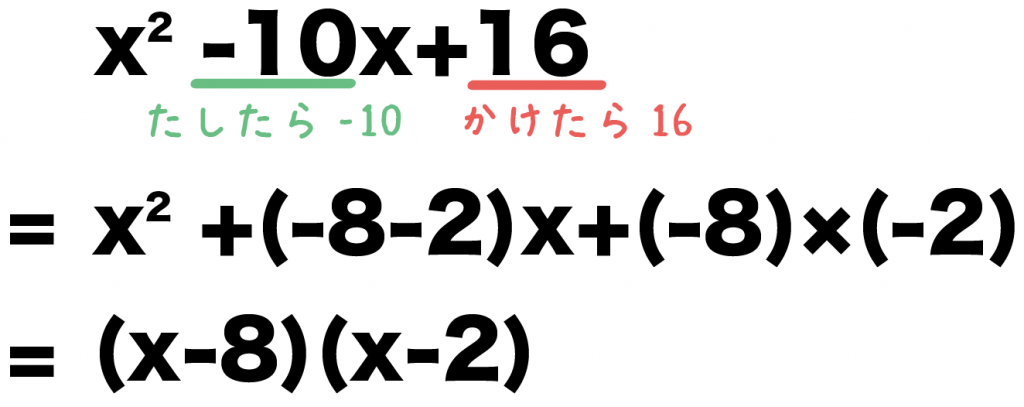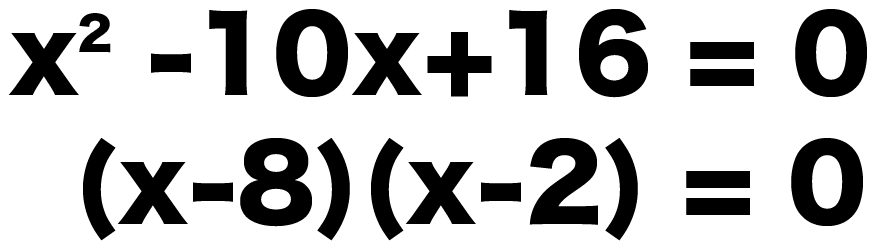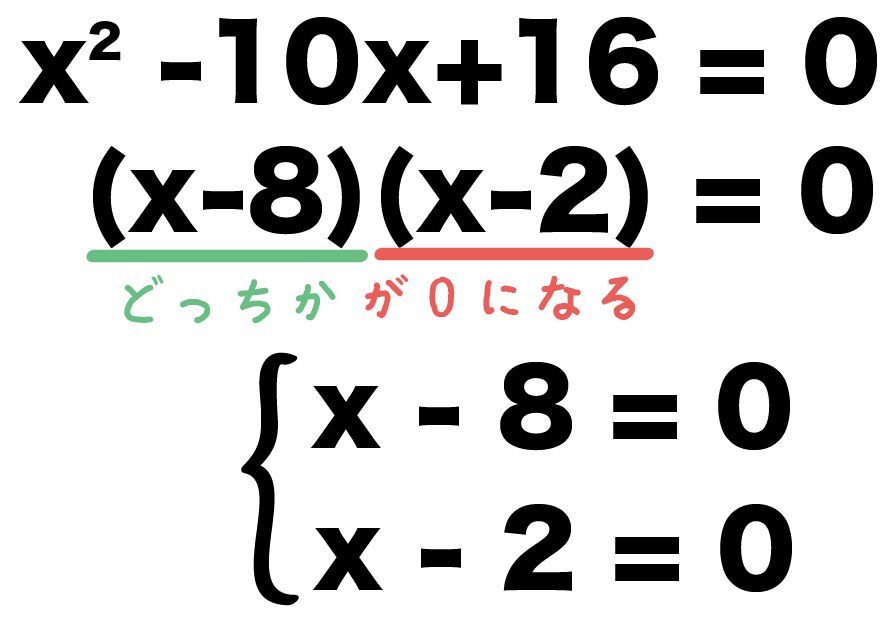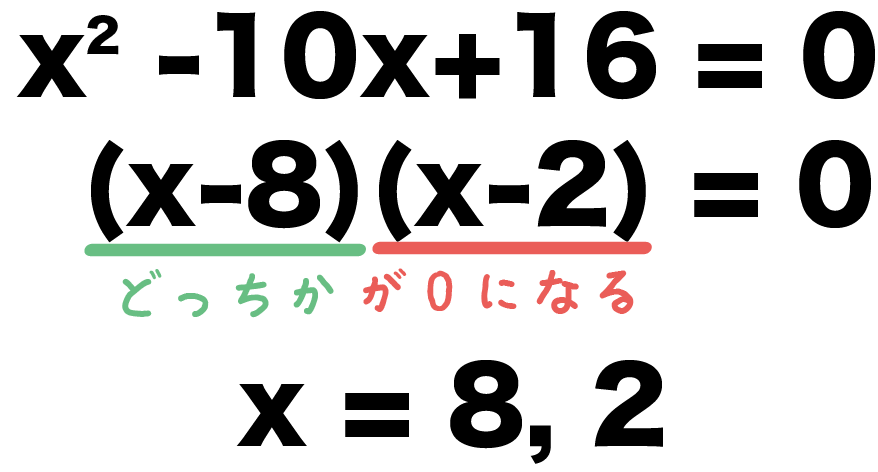二次方程式の利用の動点の問題？？

こんにちは！この記事をかいてるKenだよ。布団、押し込んだね。

 

二次方程式の利用ではいろいろ文章問題をとくよね。

整数の問題とか、長方形の面積を求める問題とか、まじありすぎる。

そんな中、テストにでてくるとヤッカイなのが、

動点の文章問題

だ。

 

動点の問題とは、

「ある点」が時間がたつにつれて辺上を動く問題のことね。

ずっと前に「一次関数の利用の問題」でやった問題といっしょ。

あれがもっかい中3数学で登場するわけ。

テストにでやすいから苦手をつぶしておこう。

 

 

二次方程式の利用の「動点」の文章問題の解き方の4ステップ

動点の文章題の解き方を紹介しよう。

つぎの練習問題をといてみようね。

 

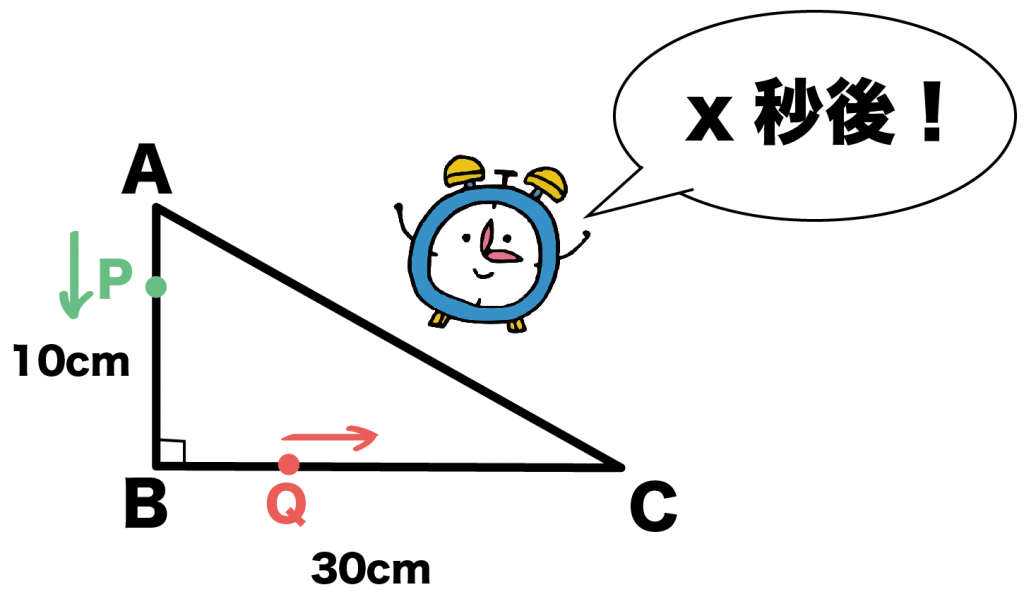
練習問題

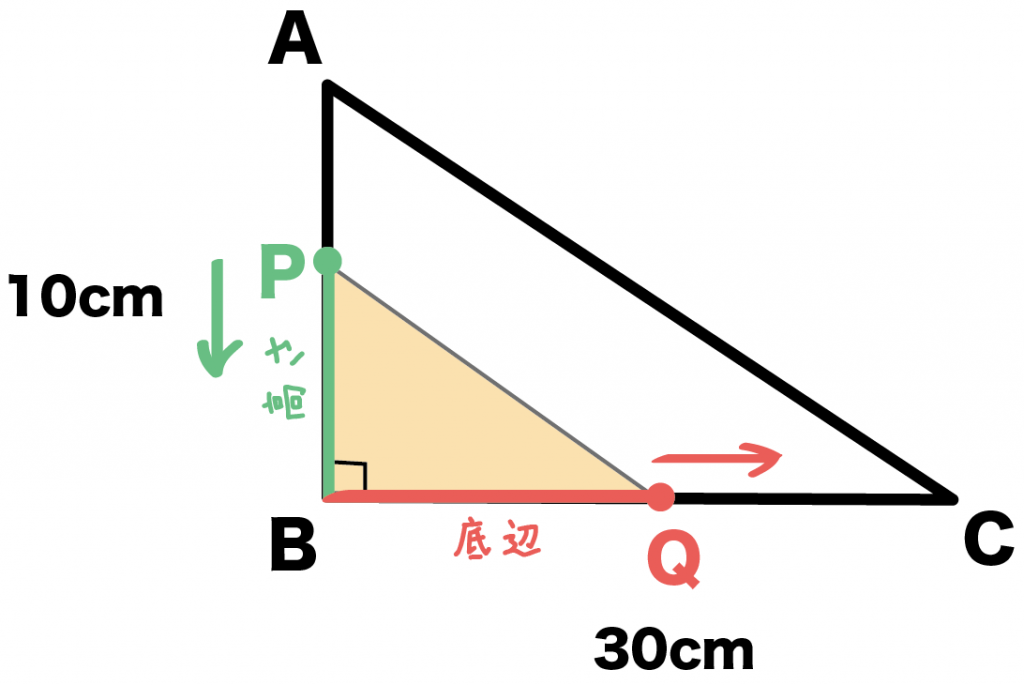
AB = 10cm、BC = 30cmの直角三角形ABCがあります。点Pは辺AB上をAからスタートして1秒間に1cmの速さでBまで動きます。また、点QはBC上をBからスタートして1秒間に2cmの速さでCまで動きます。

PとQが同時に動きはじめるとき、△PBQの面積が16cm^2になるのは何秒後になりますか？？

 

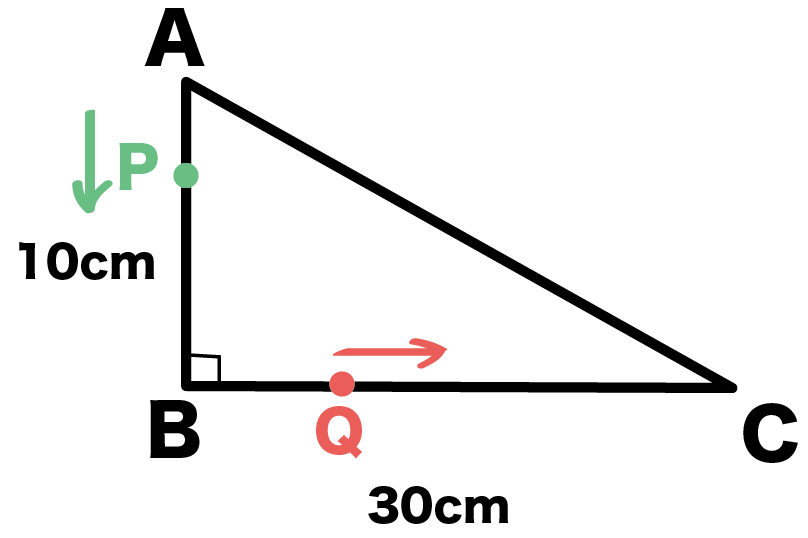
解き方は他の二次方程式の文章題といっしょ。

4ステップでいけるんだ。

1. 求めたいものを文字とおく
2. 二次方程式をたてる
3. 二次方程式を解く
4. 解のチェック

 

 

Step1. 求めたいものを文字とおく

方程式の文章題の解き方はどれもおなじ。

そう。

「文章題で求めたいもの」を文字でおけばいいんだったね？？

xでもyでもzでも好きな文字でおいてくれ。

 

例の文章問題では、

△PBQの面積が16 cm^2になるときは何秒後になるか？？

を求めたかったね。

だから、2点P、Qがスタートしてからの時間をx秒としてみようか。

 

 

これが第1ステップ。

 

 

Step2. 二次方程式をつくる

文章問題をもとに二次方程式をつくってみよう。

文章題のなかの、

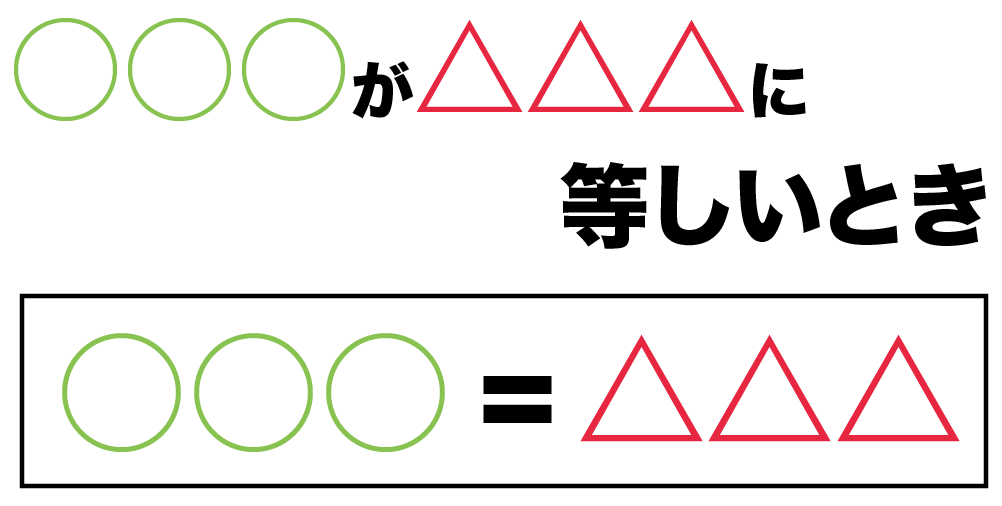
○○が△△に等しいとき

っていう文をみつけて、それをもとに、

○○ = △△

っていう方程式をつくればいいのさ。

 

 

さっきの練習問題をみてみて。

△PBQの面積が16 cm^2になるとき

っていう文がみつけられたかな？？

つまり、この二次方程式の動点の問題では、

△PBQの面積 = 16cm^2

っていう2次方程式をつくればいいわけだ。

 

それじゃあ、x秒後の△PBQの面積を計算してみよう。

 

 

三角形の面積の求め方は、

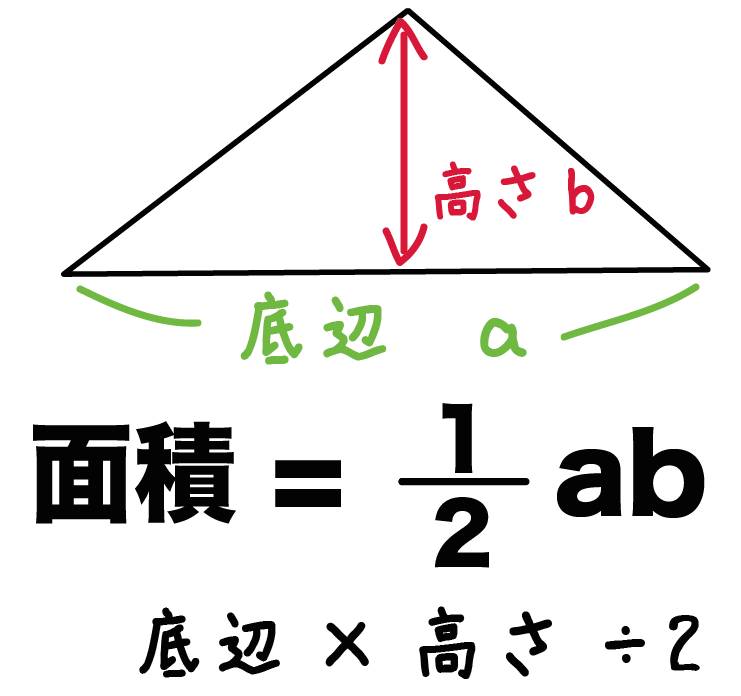
底辺×高さ÷2

だ。

 

 

ってことは、△PBQの面積を求めるには、

• PB（高さ）
• BQ（底辺）

の2つがわかってればいいね。

 

 

点P、Qはそれぞれ、

• 点P : 毎秒1cm
• 点Q : 毎秒2cm

動く。

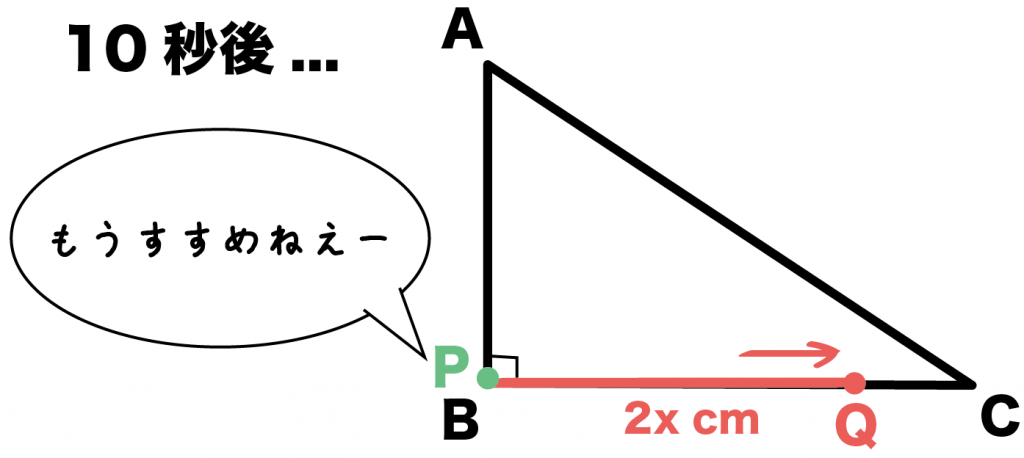
ってことは、x秒後は、それぞれ、スタート地点から、

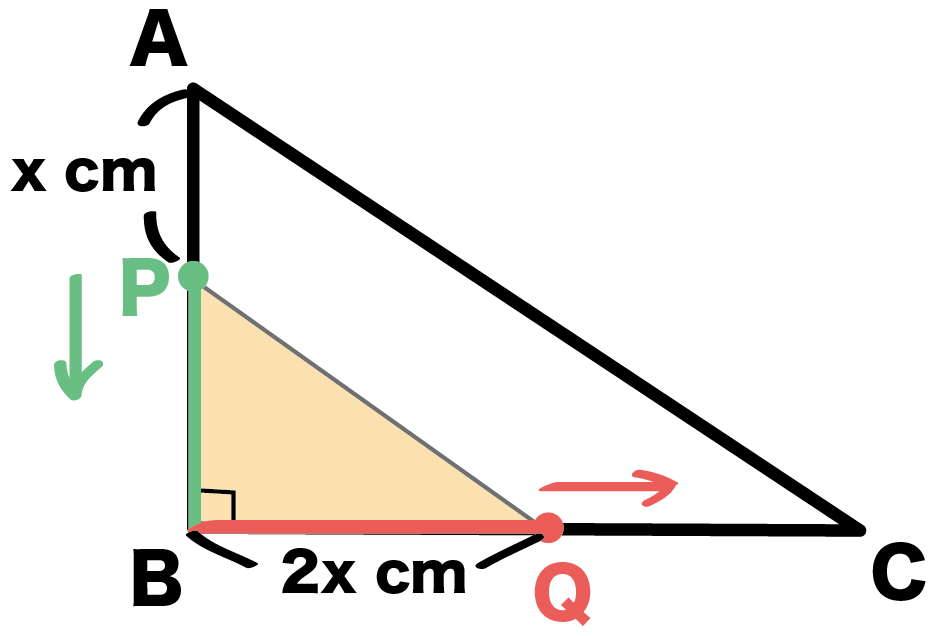
• 点P : x cm
• 点Q : 2x cm

すすんでるはずだね。

 

 

 

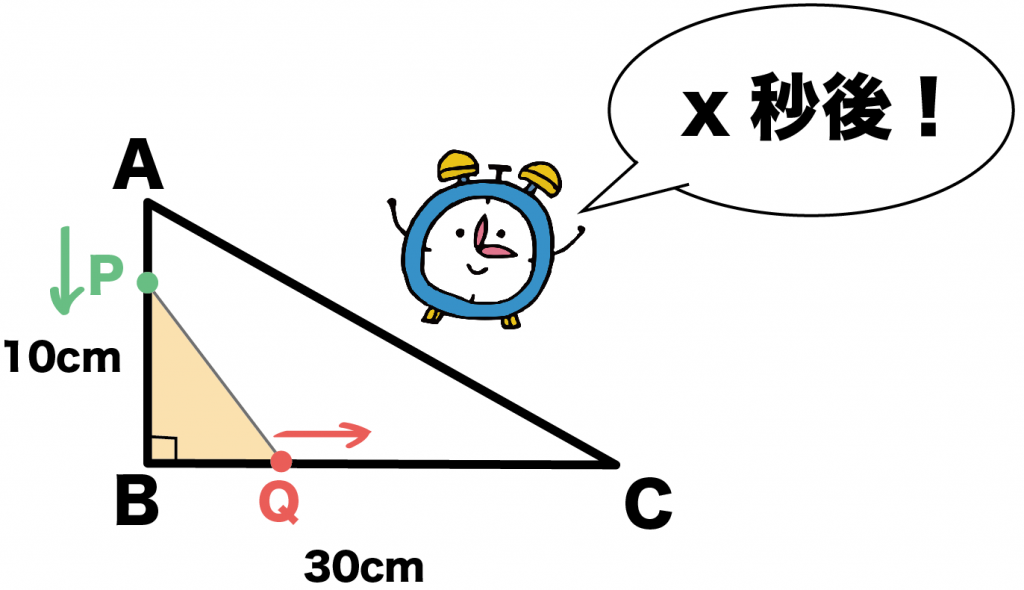
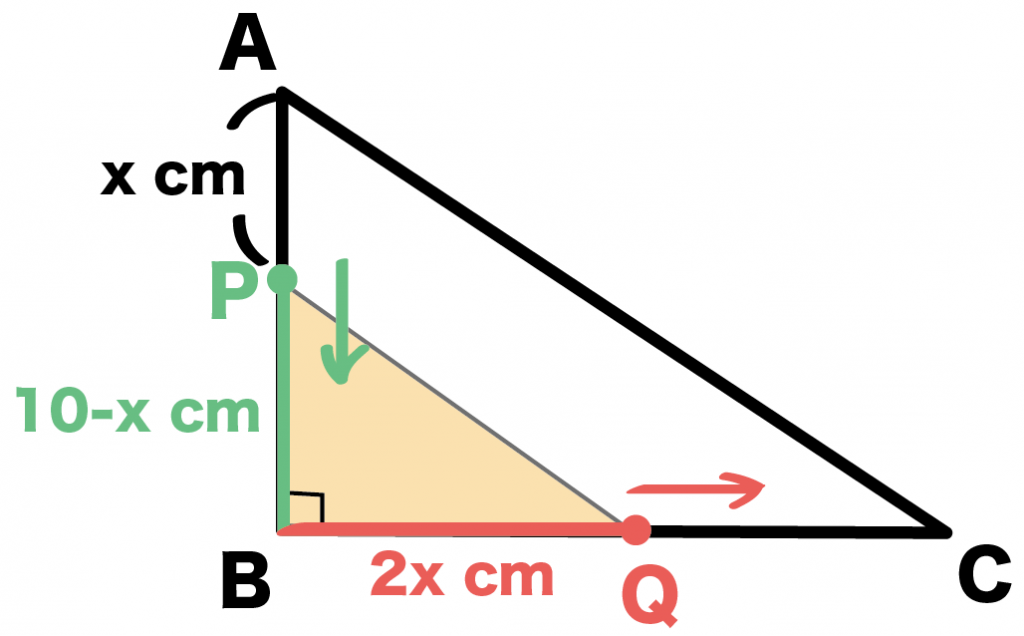
だから、直角三角形PBQの底辺と高さの辺たちは、

• PB （高さ）= AB – AP = 10 -x
• BQ（底辺） = 2x

になってる。

 

 

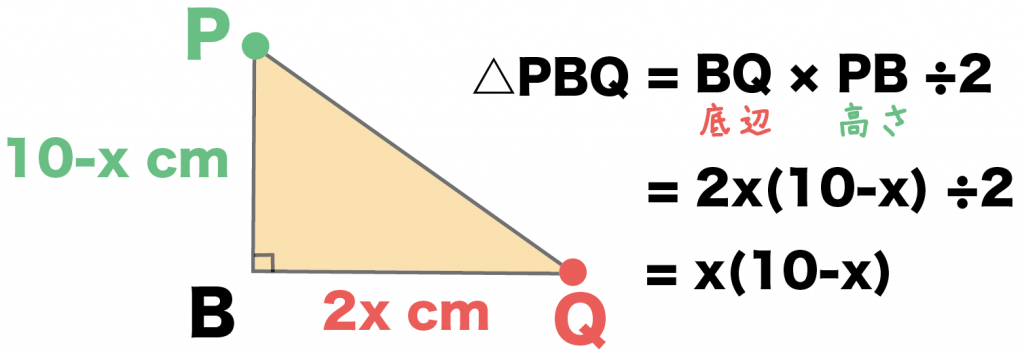
ってことは、スタートからx秒後の△PBQの面積は、

（底辺）×（高さ）÷ 2
= BQ × PB ÷ 2
= 2x (10-x)÷2
= x (10-x)

になるね。

 

 

この文章題では△PBQの面積が「16cm^2」になればいいんだったね？？

ってことは、

△PBQの面積 = 16

x (10-x) = 16

っていう二次方程式ができるはずだ。

 

 

 

 

Step3. 二次方程式を解く

さっきの二次方程式を解いてみよう。

因数分解をつかってもいいし、解の公式をつかってもいい。

とりあえず、2次方程式の解を求めてね。

 

練習問題の二次方程式は、

x (10-x) = 16

だ。

左辺の（）を分配法則で展開してやると、

x (10-x) = 16

10x – x^2 = 16

になるね。

 

 

 

移項して整理してやると、

x^2 – 10x + 16 = 0

になるんだ。

 

 

左辺の、

x^2 – 10x + 16

はどうやら因数分解の公式がつかえそうだ。

• かけたら16
• たしたら-10

になる2つの数を考えてみると・・・・

 

 

は！

• -8
• -2

ならこの条件にあいそう！

 

ってことで、因数分解の公式の、

x^2 +(a+b) x + ab = (x + a) (x +b)

 

 

で因数分解してやると、

x^2 – 10x + 16
= x^2 (-8-2)x + (-8)×(-2)
= (x -8) (x-2)

になるね。

 

 

だから、練習問題の二次方程式は、

x^2 – 10x + 16 = 0

(x -8) (x-2) = 0

になる。

 

 

( x – 8) (x – 2)が0になってるってことは、どっちかが0なはず。

よって、

• x-8 = 0
• x -2 = 0

のどちらかが成り立つはずだね？？

 

 

ってことで、2つの一次方程式をといてやると、

• x = 8
• x = 2

っていう解が2つでてくるね。

 

 

 

Step4. 解をチェックする

やった！これで二次方程式解けたー！おわたーー

ってなるのはちょっとはやい。

 

じつは、二次方程式の文章問題では最後に、

解の吟味

をしなきゃいけないんだ。

吟味ってつまり、解が文章題にそってるか確認することだ。

これをしないと、わけのわからん答えをかいちゃうからね。

 

練習問題でも解を確認しよう。

二次方程式の解は、

• x = 8
• x = 2

だったね。

つまり、PとQがスタートしてから「2秒後」と「8秒後」に面積が16cm^2になるらしい。

 

この2つのxはきちんとxの変域内におさまってるから問題なさそうだ。

だって、点PはBまでしか動けないからxの変域は、

0 ≦ x ≦ 10

だもんね。

点Pは1秒間に1cmすすむから、10秒で10cmすすむ。

つまり、終点のBに到着しちゃうのさ。

だから、xが10より大きくならないってわけ。

 

 

今回の2つの解は10以下におさまってるね。問題ない！

よって、まとめると、

△PBQの面積が16cm^2になるときはスタートしてから2秒後と8秒後だね。

 

 

まとめ：二次方程式の利用の文章題でも動点も大丈夫！！

二次方程式の利用の動点も大丈夫だ。

落ち着いて、

1. 求めたいものを文字とおく
2. 二次方程式をたてる
3. 二次方程式を解く
4. 解のチェック

の4ステップで解けばいいよ。

ただ、

解が変域内におさまってるか？？

は必ず確認してね。

そんじゃねー

Ken