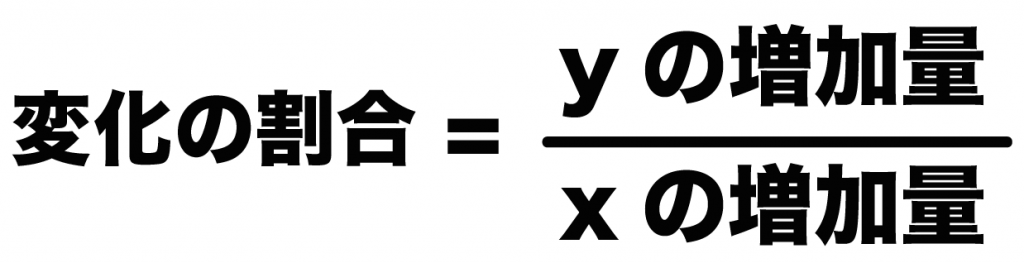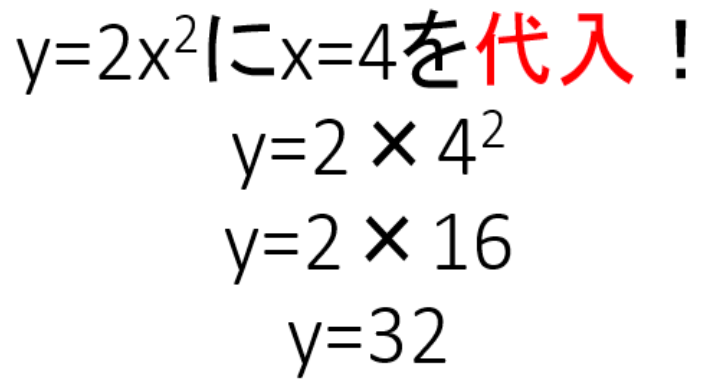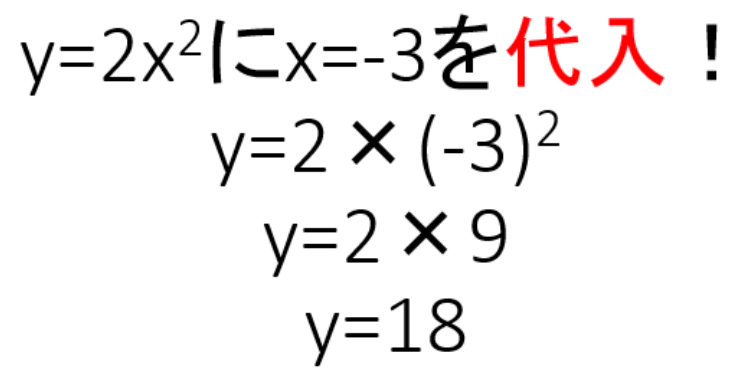二次関数の変化の割合の求め方がわかる3ステップ
二次関数の変化の割合の求め方だって??
こんにちは!ぺーたーだよ。よろしくね!
中学3年で勉強する二次関数。
入試に出てくるからマスターしたいね。
一次関数は2年生で学習したよね?
y=ax+b
ってやつ。
一方、今回勉強していく二次関数は 、
y=ax^2
という形になるんだ。
つまり、xの次数が2になってるわけね。
たとえば、y=2x^2とかy=-3x^2っていう感じで。
今日はこの、二次関数の問題でよくでてくる、
変化の割合の求め方について解説していくよ。
よかったら参考にしてみて。
=もくじ=
- 変化の割合ってなんだっけ??
- 二次関数の変化の割合の求め方
変化の割合ってなんだっけ??
変化の割合っていう言葉を復習しよう。
変化の割合とは、
xが増える量に対し、yがどれだけ増えるか(減るか)
を表すものだったね??
こいつを求めるには変化の割合の公式を使えばいいよ。
変化の割合 = (yの増加量)÷(xの増加量)
っていうやつだ。
中学3年生の二次関数でも、この公式を使うってわけね。
二次関数の変化の割合の求め方がわかる3ステップ
二次関数の変化の割合の求め方は、つぎの3ステップさ。
- xの増加量を求める
- yの増加量を求める
- 変化の割合の公式にあてはめる
練習問題をときながら勉強してみよう。
練習問題
y=2x^2でxが-3から4まで増加するときの変化の割合を求めよ。
Step1. xの増加量を求める
xの増加量を求めるには、
xの「一番大きい数」から「一番小さい数」を引けばいいんだ。
練習問題では、xは-3から4まで変化したね??
ってことは、「一番大きい数」の4から「一番小さい数」の-3を引けばいいんだ。
すると、
(一番大きい数)-(一番小さい数)
= 4-(-3)
= 7
になるね。
だから、xの増加量は7になるよ。
Step2. yの増加量を求める
次はyの増加量を求めてみよう!
え…ちょっと待って。
問題文にはyの範囲が書かれてないじゃん!
たしかにそうだね。
yの増加量は自分で計算しなきゃならないんだ。やり方は難しくないから大丈夫。
xの「一番大きい数」と「一番小さい数」のときのyの値を計算すればいいね。
まず、「y=2x^2」に「x=4」を代入してyを出してみよう。
すると、
y = 2×4^2
= 2×16
= 32
になるね。
じゃあ次は、x=-3のときのyを同じように出してみよう。
y = 2× (-3)^2
= 2×9
= 18
になるね。
ここまで来ればyの増加量はあと一歩。
xの増加量を求めるときは、一番大きい数から一番小さい数を引いたよね??
だけど、yの増加量を求めるときは注意が必要。
yの増加量は、
(xの大きい数の時のyの値)-(xの小さい数の時のyの値)
っていう計算をするんだ。
練習問題では、xの大きい数は4で、そのときのyは32。
xの小さい数は-3で、そのときyは18だったね。
よって、このときのyの増加量は、
(yの増加量)= 32 – 18 = 14
になるわけ。
(xの大きい数の時のyの値)-(xの小さい数の時のyの値)
っていうルールは絶対守ってね。
Step3. 変化の割合の公式を使う
さあ、答えは目の前だ。
後は、「変化の割合の公式」にあてはめるだけだ。
yの増加量は14、xの増加量は7だったから、
(変化の割合)
=(yの増加量)÷(xの増加量)
= 14÷7 = 2
になるね。
だから、変化の割合は2というわけさ。
これで問題はおしまいだよ。ちょっと簡単だったかな?。
もっと簡単な二次関数の変化の割合の公式がある?!
黙ってたんだけど、
二次関数y = ax2の変化の割合の求め方には便利な公式があるんだ。
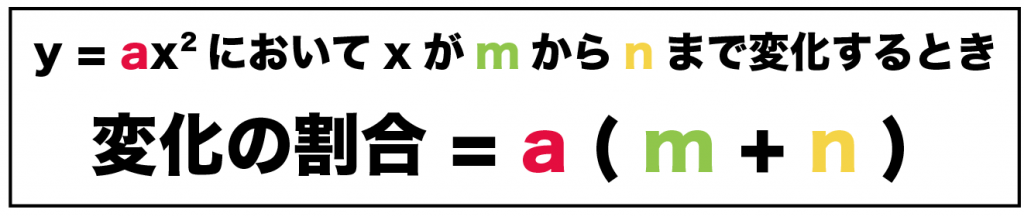
y = ax2で、xがmからnまで増加するときの変化の割合は、
a (m + n)
で計算できちゃうよ。
だから、今回の、
y = 2x^2でxが-3から4まで変化するときの変化の割合は、
2(-3 + 4)
= 2
っていうかんじで瞬殺で計算できちゃうんだ。
こんな裏技もあるんだって覚えておいてね。
⇒くわしくは「二次関数y=ax2の変化の割合の公式」をよんでくれ
二次関数の変化の割合の求め方は公式おさえればOK!
二次関数の変化の割合の求め方はどうだった??
yの増加量を求める時に注意すれば大丈夫そうだね。
最初はゆっくりでいいよ。
段々やり方をマスターしていこうね!
それじゃ、また。
ぺーたー