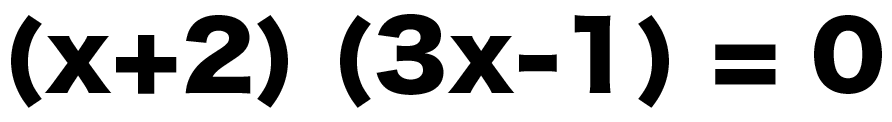たすきがけ因数分解で二次方程式を解く5つのステップ
たすきがけ因数分解で二次方程式は解ける??
ある日、数学が苦手なかなちゃんは、つぎの二次方程式に出会いました。
練習問題
つぎの二次方程式を解きなさい。
3x^2 + 5x -2 = 0
この二次方程式って因数分解の公式つかえないの・・・・
せっかく解き方おぼえたのに。。
ど、ど、どうしよう!!
こりゃむずいわ
そもそも、たすきがけの因数分解ってなに??
因数分解の技の1つだね!
因数分解するときに、たすきがけみたいに掛け算して考えるから、「たすきがけ」って呼ばれてるんだ。
簡単にいうと、
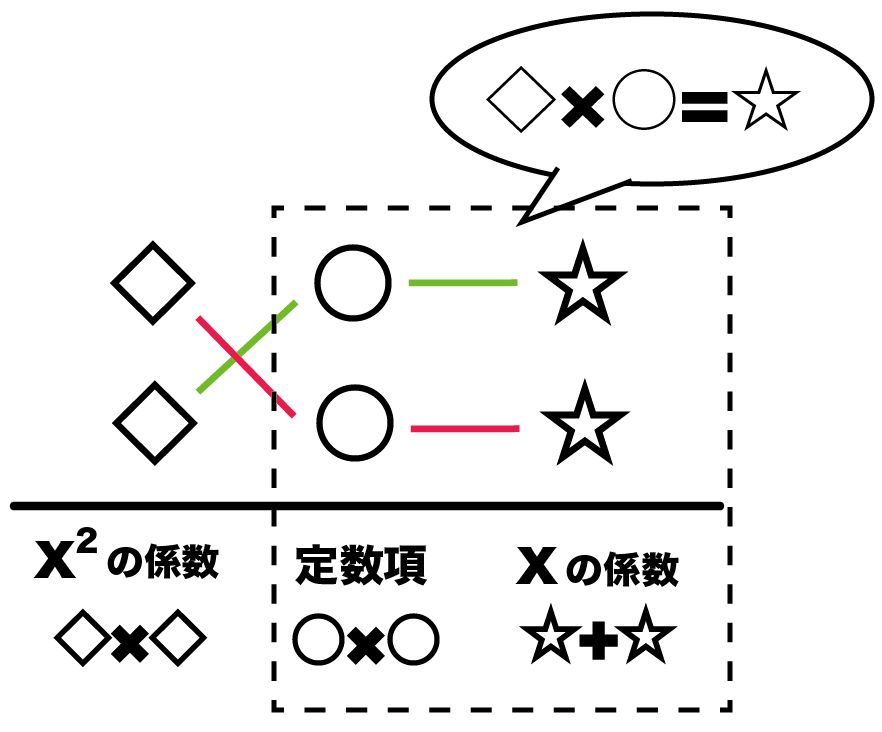
「かけたらxの2乗の係数になる数字の組」と「かけたら定数項になる数字の組」と、「たしたらxの係数になる組」を、
◇×○=☆
になるようにならびかえるんだ↓↓
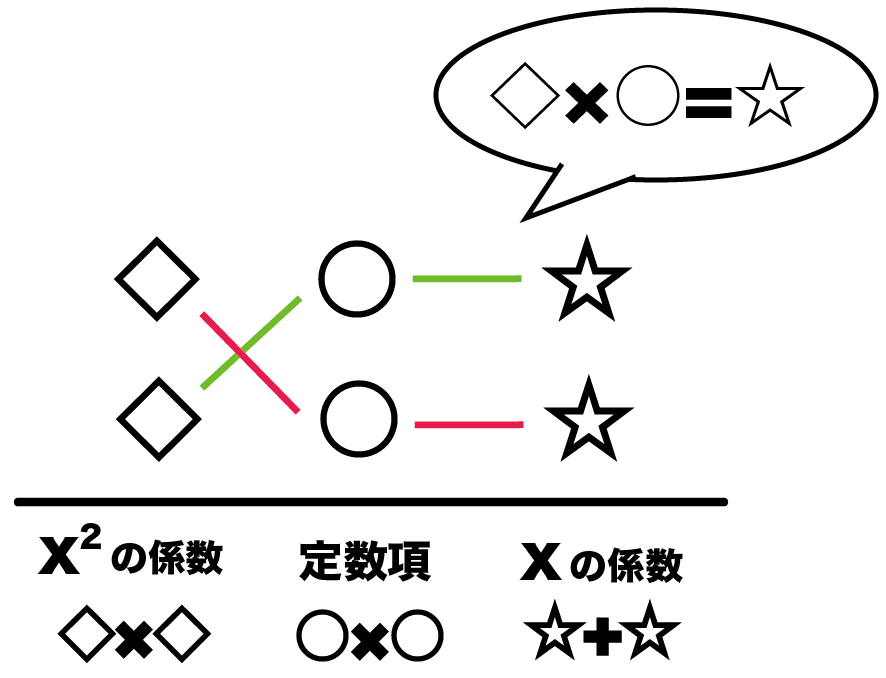
Step1.『係数』と『定数項』の確認!
たすきがけ因数分解は、パズルみたいに数字をあてはめていくから、数字の確認がすごく重要なんだ。
定数項・・・!?
定数項は「数字だけの項」だったよね??

Step2.組み合わせを見つけよう!
まずは一番左の「xの2乗の係数」からだね。
かけたら「3」になる2つの数字の組み合わせは・・・・
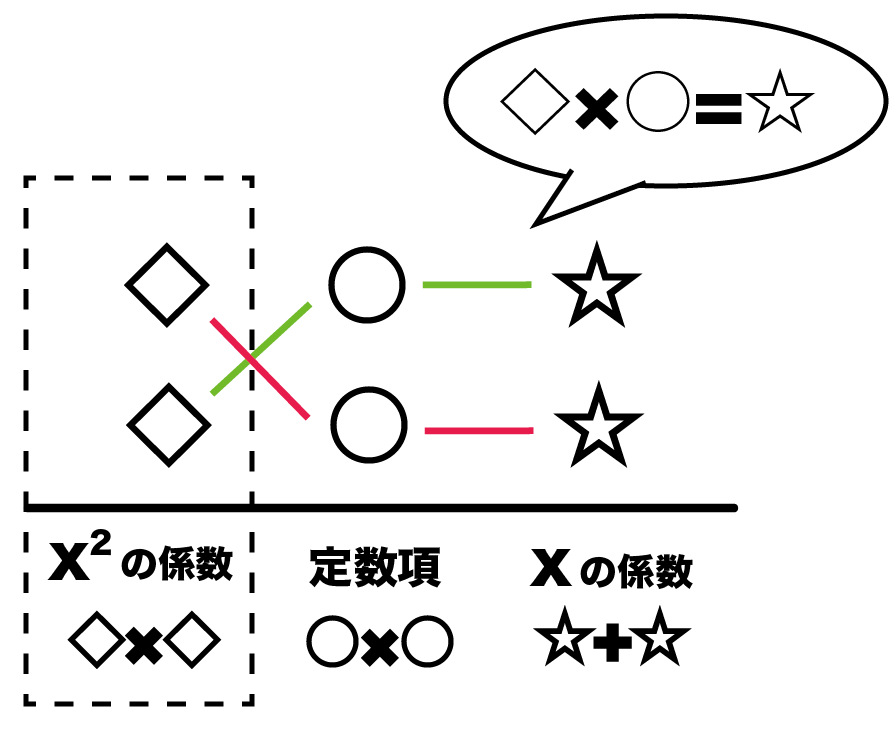
じつは、「-1×-3」もあるんだけどね。
「x²の係数」は正の数のことしか考えなくていい
っておぼえてとくといいよ。
これなら組み合わせのパターンを減らせるよね。
秘密技♪
- 1×-2
- -1×2
のどっちかかな?
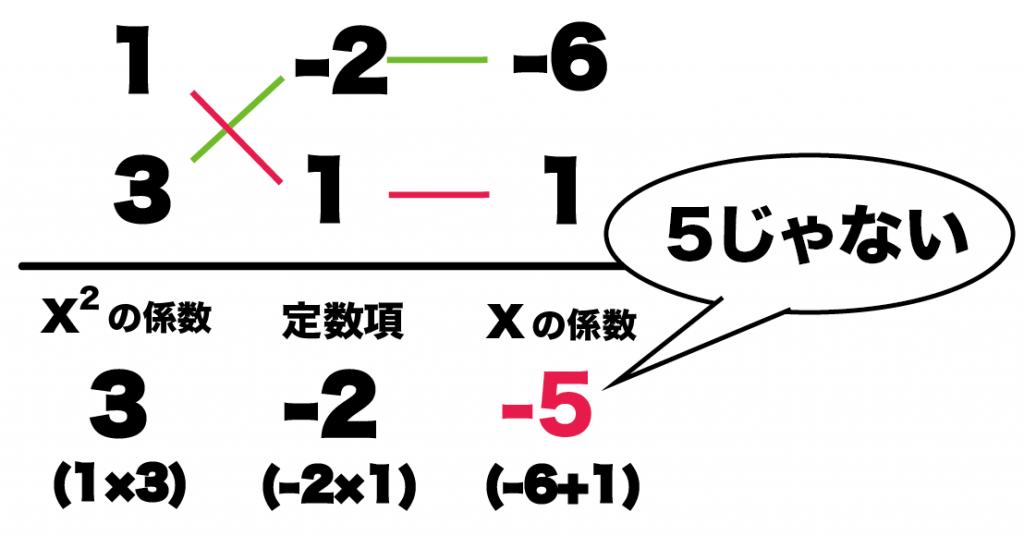
あと、☆の組み合わせは・・・いっぱいあるじゃん!たして5になる組み合わせなんて!!
Step3. 組み合わせを考えよう
☆になる組み合わせにすればいいの
例えば、○の組合せを1×-2にすると?
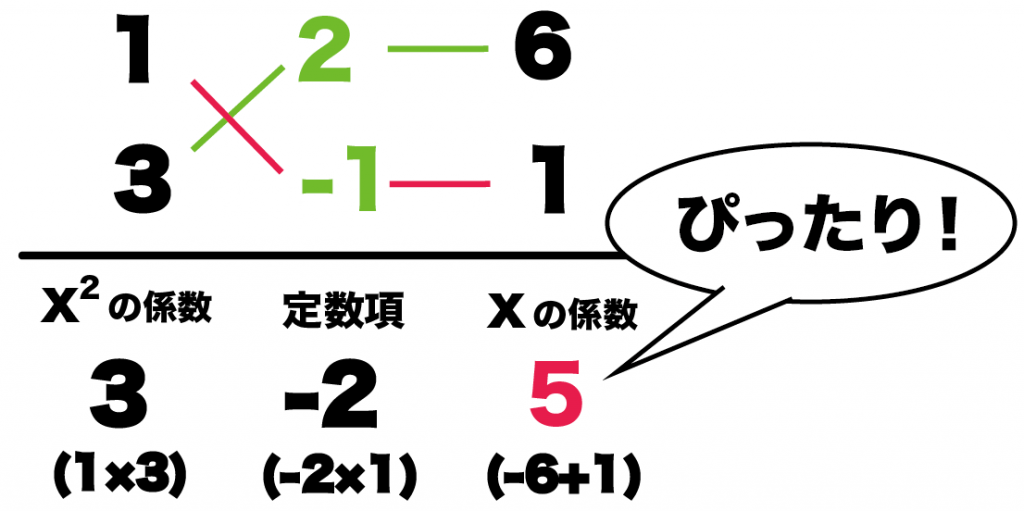
Step4. 係数をもどす
◇と○にはいった数字の組み合わせを()にいれるだけなんだ。
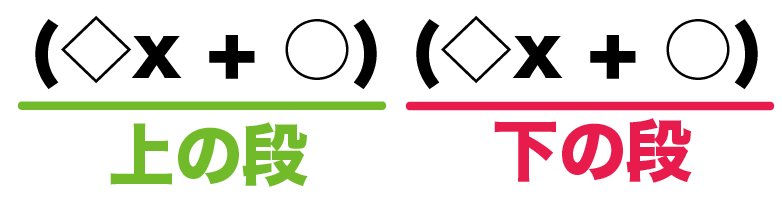
【上】(◇x+○)【下】(◇x+○)
ってなるようにいれてみて!
あと、忘れちゃいけないのが右辺!
(x+2) (3x-1) = 0 ってなるよ♪
Step5. 二次方程式を解く!
カッコの中が、どっちか0になればいいから、
xは「-2」と「3分の1」かな?
x = -2, 3分の1
ってかけば完ぺきだね☆
二次方程式をたすきがけで解けるとかっこいい!
- 係数と定数項の確認
- 組み合わせをみつける
- あてはめる
- かっこへGO
- 二次方程式を解く
かっこがある式にするためのものなんだ!!
かっこがある式……あっ、先生、
もしかして、『かっこいい』とかけてたの!?
それもあるけど、たすきがけ使いこなせたら、かっこいいよ!だから!!
何度も挑戦して慣れていこう!
☆練習問題☆
- 2x² – 5x+7 = 0
- 3x²+5x+2= 0
- 4x²-11x+ 6 = 0
- -2x²-x + 6 = 0