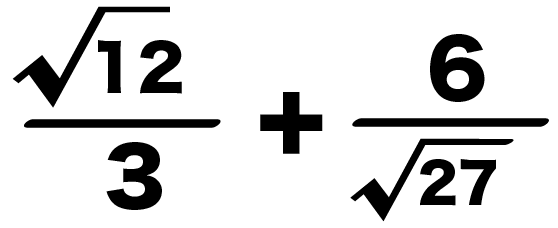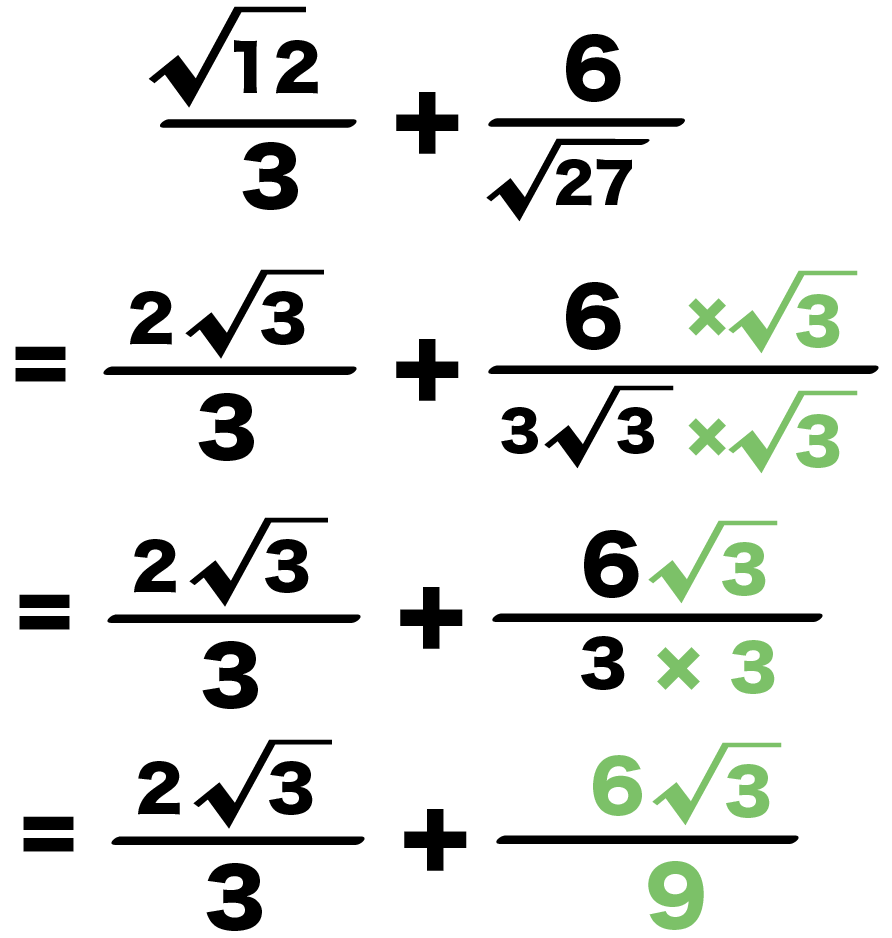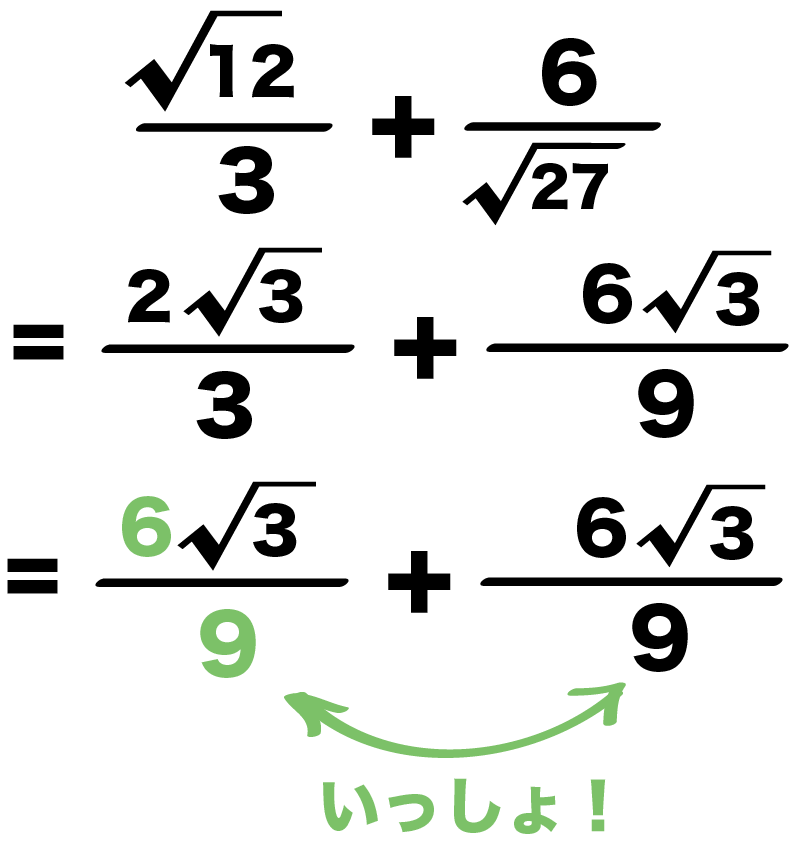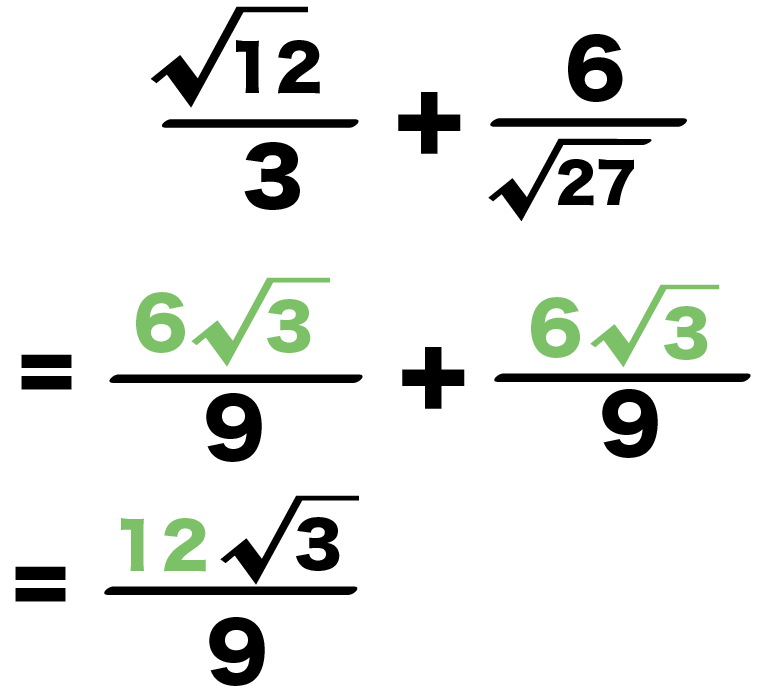ルート（平方根）の分数の足し算・引き算の計算方法って！？？
こんにちは！この記事をかいてるKenだよ。どら焼きは脳にきくね。
ルートの計算には色々ある。
なかでも、いちばんむずいのは、
ルート（平方根）の分数の計算
だ。
ただでさえ、ルートの計算で精一杯。
なのに、そ、それを分数にしちゃうんだもん！？
クソやっかいだね。
今日は、ルート分数の計算をマスターするために、
平方根の分数の足し算・引き算の計算の仕方
を5ステップで解説していくよ。
ルートの分数の足し算・引き算の仕方5ステップ
さっそく計算方法を紹介していくよ。
5ステップで分数の足し算・引き算ができちゃうんだ。
- ルートを簡単にする
- 分母の有理化
- 通分する
- 足し算・引き算
- 約分する
例題をといてみよう。
つぎの平方根の分数の計算をしなさい。
3分の√12 + √27分の6
Step1. ルートを簡単にする
ルートを簡単にしよう。
ルートの中身から、2乗の因数をとりだせばいいのさ。
⇒ くわしくは「ルートを簡単にする方法」を読んでみてね。
例題の計算式では、
- √12
- √27
を簡単にできそう。
なぜなら、
ルートの中に2乗の因数がふくまれてるからね。
√12だったら、2の2乗、
√27だったら3の2乗が入ってる。
それぞれ簡単にすると、
3分の√12 + √27分の6
= 3分の2√3 + 3√3分の6
になるね。
これが第1ステップ！
Step2. 分母を有理化する
つぎは、分母の有理化だ。
分母からルート（無理数）をなくせばいいんだ。
⇒ くわしくは「分母の有理化」をよんでみて。
例題をみると、
2つめの項の分母に「√3」があるね。
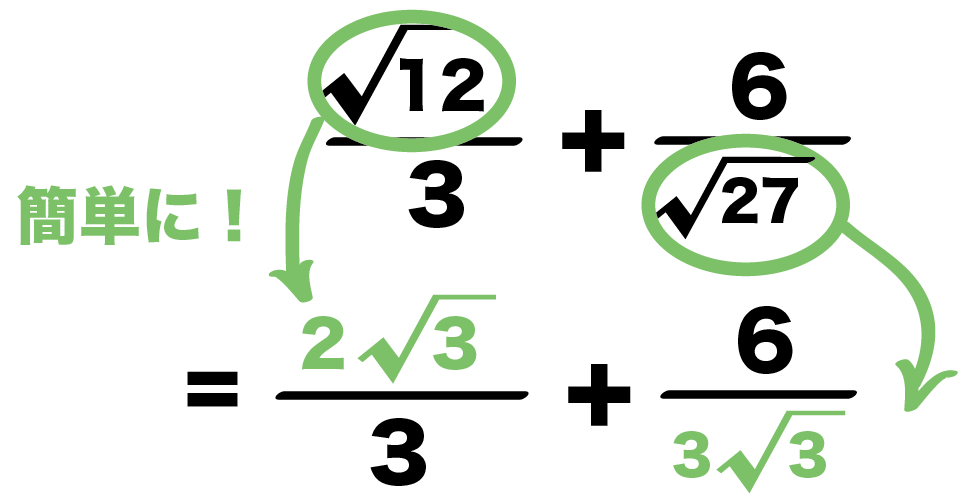
このルートをなくすために、
分母と分子に「√3」をかけるんだ。
すると、例題のルート計算式は、
3分の√12 + √27分の6
= 3分の2√3 + 3√3分の6
= 3分の2√3 + 9分の6√3
になる！
Step3. 通分する
つぎは、通分しよう。
通分ってようは、
分数たちの分母をそろえる
ってことさ。
例題の分数たちはそれぞれ、
- 3分の2√3
- 9分の6√3
だったよね？？
これじゃあ分母が「3」と「9」でバラバラだ。
分母を最小公倍数の9にあわしてやると、
- 3分の2√3 = 9分の6√3
- 9分の6√3
になるね！
Step4. 足し算・引き算する
つぎは分子を足し算・引き算しちゃおう。
例題でも分子を足し算してやると、
3分の√12 + √27分の6
= 9分の6√3 + 9分の6√3
= 9分の12√3
になるね。
Step5. 約分する
最後は、ルートの分数を約分してみよう。
約分してすっきりしたほうがいいじゃん？
例題でも計算結果の、
9分の12√3
を約分しよう。
分母の「9」と分子の「12」の共通の約数に3がある。
ってことは、3で約分できるはずだから、
9分の12√3
= 3分の4√3
になるね。
これでルートの分数の計算は終了だ！
まとめ：ルートの分数の計算は総合格闘技だ！
平方根の分数の足し算・引き算はどうだったかな？
5ステップもあってむずそうだけど、使っているのはどれも過去のワザ。
スムーズにとけるように踏ん張ってみよう。
最後に練習問題を用意したから、よかったら解いてみてね。
練習問題
つぎの平方根の計算をしなさい。
√3分の4 – √2分の1 + 6分の√2
そんじゃねー
Ken
