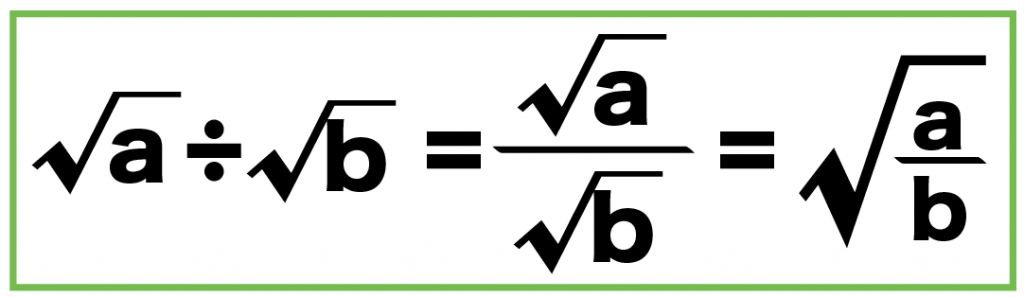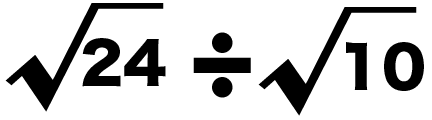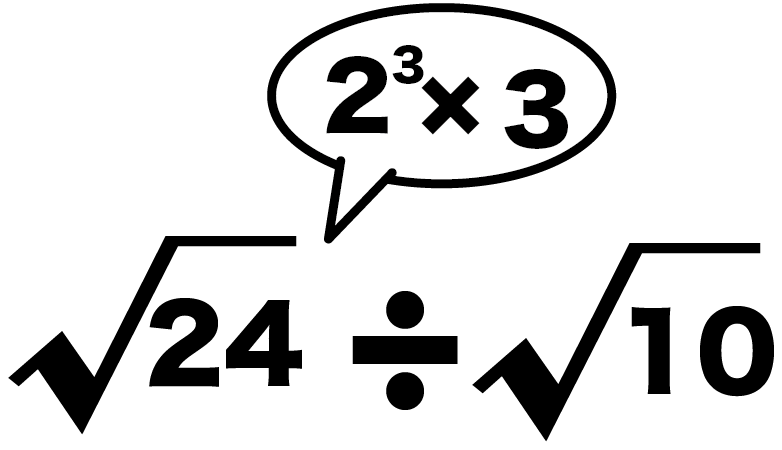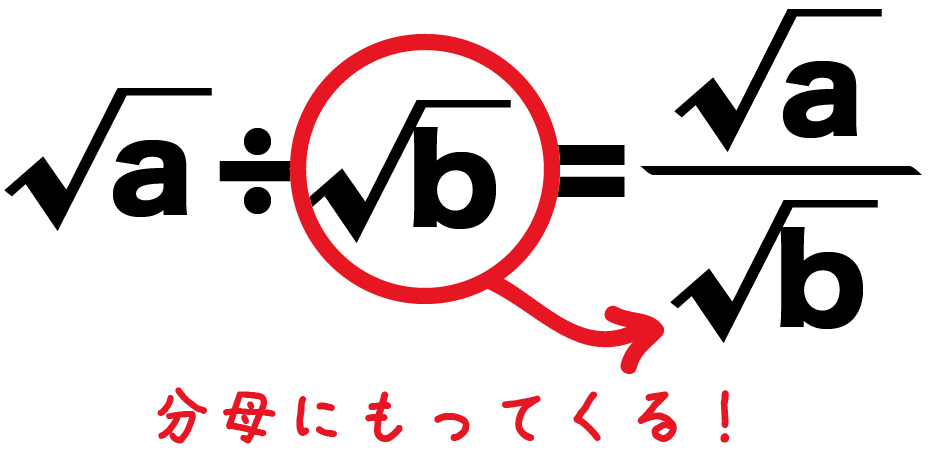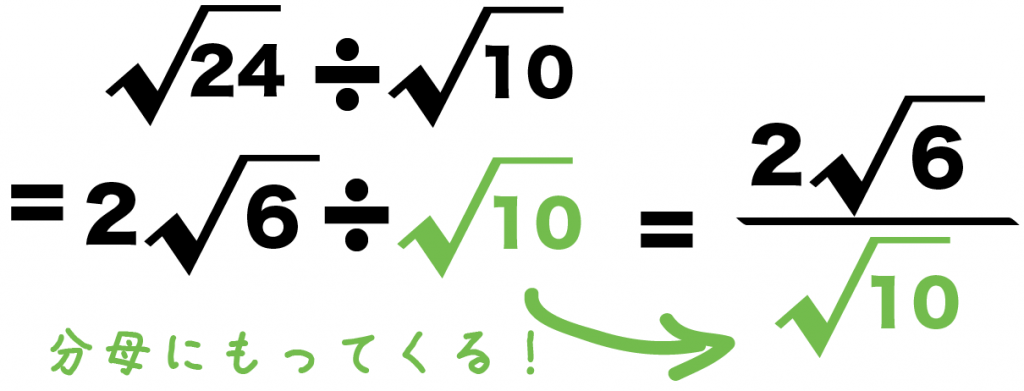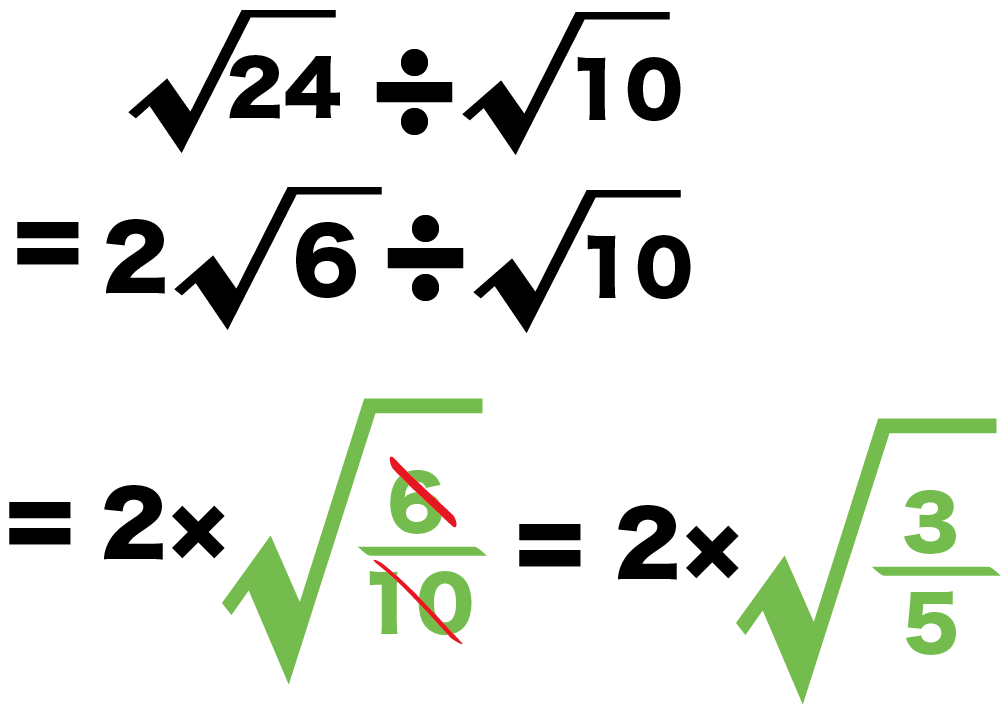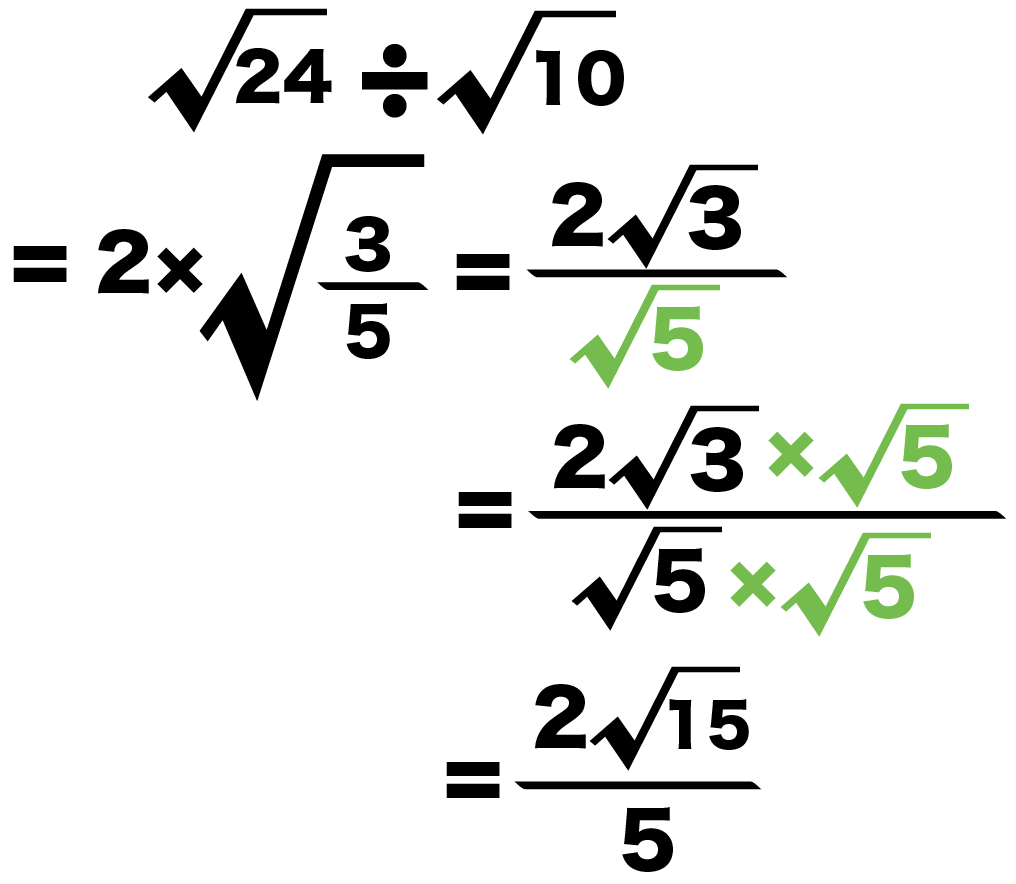平方根(ルート)の割り算の計算方法の5つのステップ
平方根(ルート)の割り算の計算方法がわからん!?
こんにちは!この記事をかいてるKenだよ。湿度はほどほどね。
ルートの計算にはいろいろある。
足し算、引き算、掛け算・・・って感じでさ。
もうね、ありすぎて疲れちまうよ。
今日はルート計算をマスターするために、
ルート(平方根)の割り算の仕方
を勉強していこう。
= もくじ =
- ルート割り算の基本ルール
- 割り算の計算方法
ルート(平方根)割り算の基本ルール!
ルートの割り算には基本ルールがある。
それは、
分子・分母のルートをいっしょにしてもいい
ってやつだ。
たとえば、√a、√bがあったとすると、
√b 分の √a = √(b分のa)
になる。
えっ。これが割り算と関係があるのかッテ??!
そうだね。
割り算は分数であらわせたよね。
a÷b
なら
b分のa
って感じで。
÷のうしろの数を分母に、それ以外を分子にもってきてるわけ。
これをルートの割り算でもつかうと、
√a÷√b = √b分の√a
になるんだ。
んで、これにさっきのルールでつかうと、
√a÷√b = √b分の√a = √(b分のa)
になる。
そして、途中の真ん中をはぶくと、
√a÷√b =√(b分のa)
になるね。
つまり、
√をいっしょにして、÷の後ろを分母にしてもいいんだ。
これがルート割り算の基本ルールだ。
平方根(ルート)の割り算の5つのステップ
ルートの割り算は5ステップでいけるよ。
- ルートを簡単にする
- 割り算を分数にする
- ルートを一緒にする
- 約分する
- 分母を有理化する
例題をいっしょにといてみよう。
例題
つぎのルートの割り算を計算してください。
√24 ÷ √10
Step1. ルートを簡単にする
ルートを簡単にしよう。
ルートの中身から2乗の因数を外にだせばいいんだ。
⇒ ルートを簡単にする方法はコチラ
例題では、
ルート24
が簡単にできそうだね??
なぜなら、素因数分解すると、
24 = 2の3乗 × 3
になるからね。
ルートの外に「2の2乗」をとりだせそうだ。
√24を簡単にすると、
√24 ÷√10
= 2√6 ÷ √10
になるね!
Step2. 割り算を分数にする
割り算を分数にしよう。
やり方は簡単。
「÷の後ろの数」を分母にもってくればいいのさ。
√a÷√bなら、
√b分の√a
ってかんじにできる。
例題の割り算では、
√10
が÷の後ろにきてるね??
だから、こいつを分母にもってくると、
√24 ÷ √10
= 2√6 ÷ √10
=√10分の2√6
になるよ。
Step3. ルートを1つにする
分数を1つにまとめよう。
√b 分の √a = √(b分のa)
っていう基本ルールをつかえばいいのさ。
例題でもおなじ。
√10分の√6
のルートをいっしょにしてあげると、
√24 ÷ √10
=√10分の2√6
= 2×√(10分の6)
になるね!
Step4. 約分する
ルートの中身を約分しよう!
スッキリしていいじゃん!?
例題のルート内の分数は、
10分の6
だね??
こいつを約分すると、
5分の3
になる。
だから、さっきの計算式は、
√24 ÷ √10
= 2×√(10分の6)
= 2×√(5分の3)
になるんだ。
Step5. 分母を有理化する
最後に、分母を有理化しよう。
分母の平方根を分子と分母にかければいいのさ。
⇒くわしくは「分母の有理化のやり方」を読んでみてね。
例題の分母は√5。
だから、分子と分母に√5をかけると、
√24 ÷ √10
= 2×√(5分の3)
= 5分の2√15
になるね。
おめでとう!
これでルートの割り算マスターだ。
まとめ:ルートの割り算の計算方法は長い
平方根の割り算の仕方はどう??
5ステップあるからなげえかもしれない。
だけど、どのステップも基本的なこと。
ルートの割り算に必要なものをしっかり
とおさえてこう。
そんじゃねー
Ken