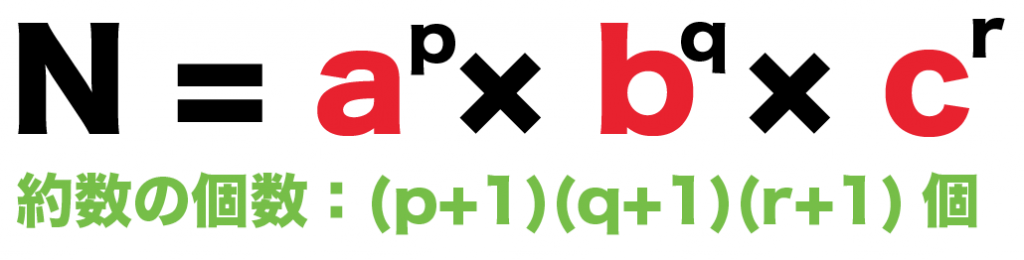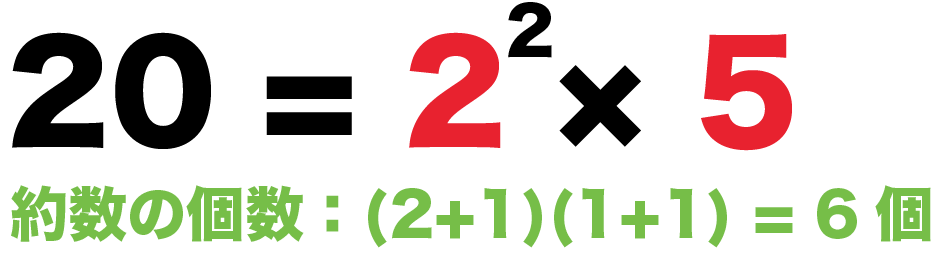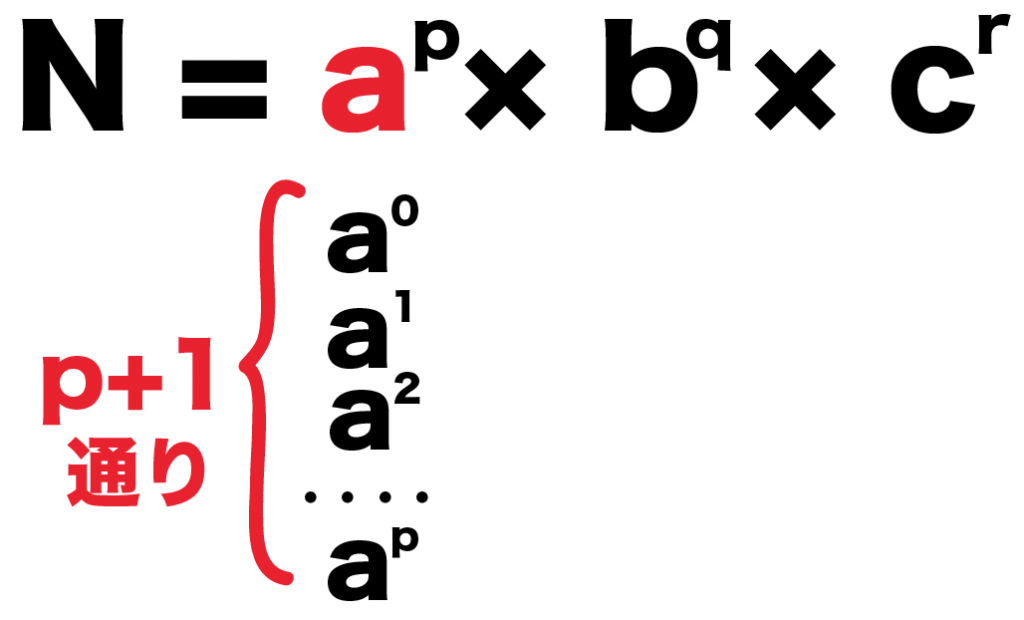【中学数学】正の約数の個数の求め方がわかる3ステップ
正の約数の個数の求め方を知りたい!?
こんにちは!この記事をかいてるKenだよ。植物は癒しだね。
正の約数の個数を求めたい。
そんなとき・・あるよね。。
小さい数の約数なら簡単。
たとえば、
- 2の約数:1と2(2個)
- 8の約数:1, 2, 4, 8(4個)
- 20の約数:1, 2, 4, 5, 10, 20 (6個)
みたいなかんじで、がんばれば約数の個数はわかっちゃう。
だけどね。
むちゃでかい自然数の正の約数の個数を求めたいとき。
こいつはそう簡単にうまくいかない。
たとえば、360の約数の個数を求める問題。
1, 2, 3, ,,,4, ,5, ,,,, 6,,,,,,12,,,,,
って数えてたら日がくれちゃうね。気合だけじゃのりきれない。
そこで今日は、どんなに大きな数でも使える、
約数の個数の求め方の公式
を紹介するよ。
よかったら参考にしてみて。
正の約数の個数の求め方がわかる3ステップ
正の約数の求め方には公式があるよ。
約数の個数を求めたい自然数をNとしよう。
んで、
N = a^p × b^q × c^r
って素因数分解できたとする。
すると、正の約数の個数は、
(p+1)(q+1)(r+1)
になるんだ。
つまり、
(素因数の指数+1)をかけあわせるだけでいいんだ。
たとえば、自然数20の約数の個数を求めてみよう。
こいつを素因数分解すると、
20 = 2^2 × 5
になるね。
正の約数の個数は、(指数+1)をかけあわせればいいから、
(2+1)×(1+1)
= 6
になるってわけ。
今日はこの公式になれるため、20よりもう少し大きい、
360
の約数の個数をもとめてみよう!
つぎの3ステップで約数の個数を求めることができるよ。
- 素因数分解する
- 指数をかぞえる
- (指数+1)をかけあわせる
Step1. 素因数分解する
自然数を素因数分解してみよう。
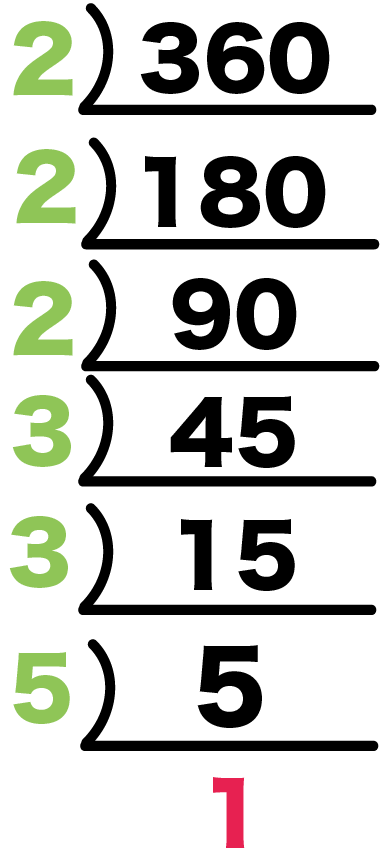
360を素因数分解してやると、
- 360÷2 = 180
- 180÷2 = 90
- 90÷2 = 45
- 45÷3 = 15
- 15÷3 = 5
- 5÷5=1
・・っおっと。
1がでてきたのでここでストップだね。
わった素数をあつめて因数にすると、
360 = 2^3 × 3^2 × 5
になるね!
Step2. 指数をかぞえる
つぎは、素因数の指数をかぞえよう。
自然数の360は、
360 = 2^3 × 3^2 × 5
になったね。
素因数の指数に注目してやると、
- 2の指数:3
- 3の指数:2
- 5の指数:1
になってるね。
Step3. (指数+1)をかけあわせる
最後は、
指数に1をたしたもの
を掛け合わせてみよう。
360の素因数の指数はそれぞれ、
- 2の指数:3
- 3の指数:2
- 5の指数:1
だったよね??
だから、360の正の約数の個数は、
(2の約数の個数+1) × (3の約数の個数) × (5の約数の個数)
= (3+1) × (2+1) × (1+1)
= 24
になる。
つまり、360の正の約数の個数は「24」になるってわけ!
なんで約数の個数が求められるの??
でもさ、ちょっとあやしくない??
約数の個数の求め方が、こんなに簡単だなんて・・・
じつは、
「 約数の個数」=「それぞれの素因数をかけるパターン数」
なんだ。
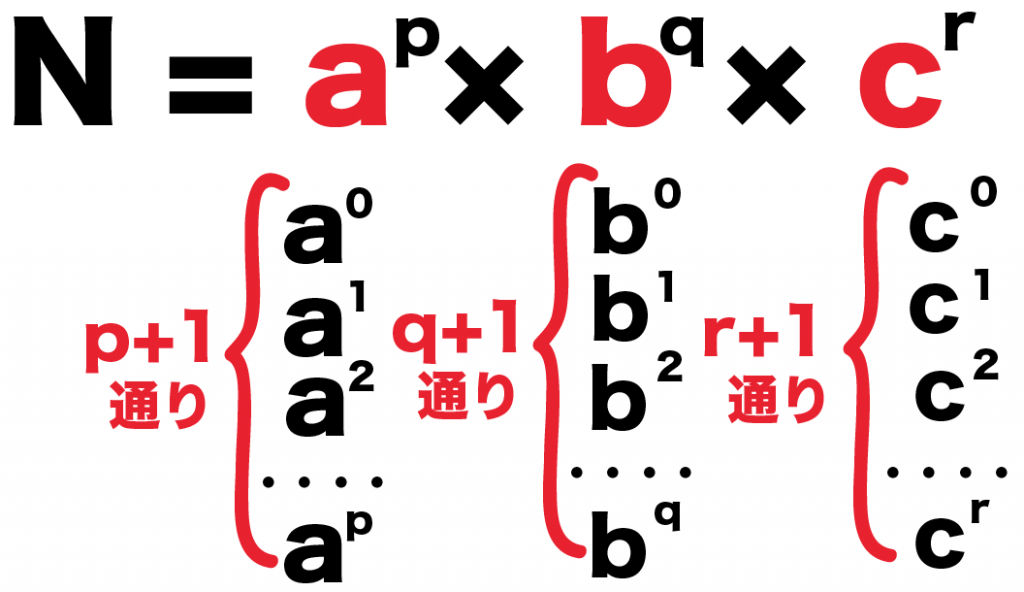
たとえば、さっきの自然数Nが、
N = a^p × b^q × c^r
に素因数分解できるとしよう。
このとき、素因数aの掛け方の方法は、
- aの0乗
- aの1乗
- aの2乗
- ・・・
- aのp乗
の (p+1)通りあるはず。
おなじように、他の素因数も考えてやると、
- bの掛け方のパターン: q + 1通り
- cの掛け方のパターン: r + 1 通り
になるはずだ。
1つの素因数あたりの指数のパターンは、
- p+1 通り
- q+1 通り
- r+1 通り
ある。
だから、自然数Nの約数の個数は、
(p+1)×(q+1)×(r+1)
になるんだ。
どう??しっくりきたかな??
まとめ:正の約数の個数の求め方は素因数分解からはじまる!
約数の個数??
そんなの簡単さ。
素因数分解して、指数に1をたして、かけあわせればいいんだ。
じゃんじゃん素因数分解していこう!
そんじゃねー
Ken