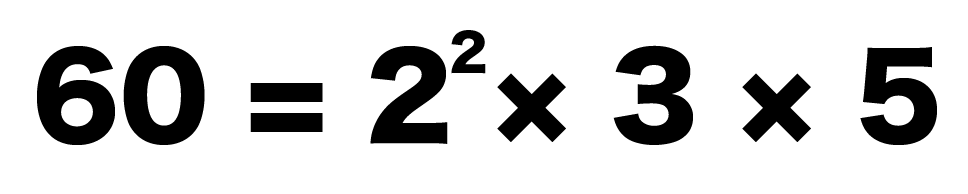素因数分解の応用問題の解き方がわかる3つのステップ
素因数分解の応用問題の解き方を知りたい!
こんにちは!この記事をかいているKenだよ。シチリアに行きたいね。
素因数分解の問題はたーくさんあるよ。
ほとんどの問題はただ素因数分解するだけ。
でもたまーに、
素因数分解の応用問題がでてくるよ。
たとえば、つぎのようなやつね↓↓
今日はこの応用問題を3ステップで解説していくよ。
よかったら参考にしてみてね。
素因数分解の応用問題の解き方がわかる3つのステップ
例題をいっしょにといてみよう。
3ステップでとけちゃうよ。
- 素因数分解する
- 指数が奇数になってる素因数をみつける
- 指数を偶数にするためにかける数を考える
Step1. 素因数分解する
まず素因数分解してみよう。
素因数分解のやり方で分解すればいいんだ。
例題では、60を素因数分解してみよう。
素因数分解の解き方の鉄則は、
小さい素数から順番にわっていく
だったよね??
だから、いちばん小さい素数の2から割りはじめよう。
割り算の答えが「1」になるまで素数で割り続けてみてね。
すると、
- 60÷2 = 30
- 30÷2 = 15
- 15÷3 = 5
- 5÷5 = 1
になるはず。
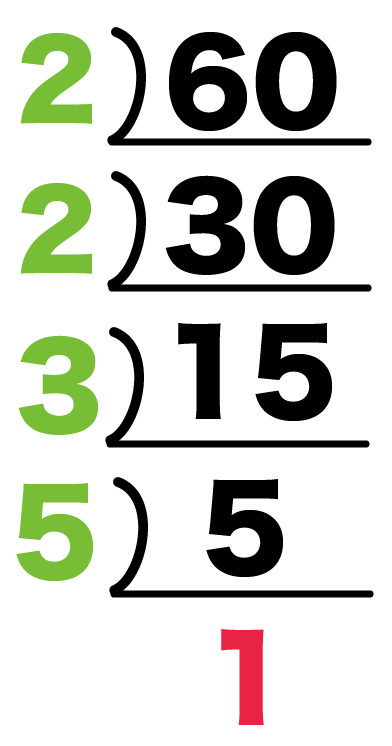
あとはわった素数をあつめて「×」で結んでみて。
すると、
60 = 2^2 × 3 × 5
になるね!
Step2. 指数が奇数の素因数をさがす!
つぎは、素因数のなかから、
指数が奇数になってるやつ
をさがそう。
60の素因数のうち、
- 3
- 5
の指数は奇数だね。
これが第2ステップ!
Step3. 指数が奇数の因数を1つずつかける
最後は、
指数が奇数の素因数を1つずつかけてみよう!
それが答えになるよ。
なぜなら、すべての素因数の指数を偶数にすれば、
「○○の二乗」になるからね。
例題をみてみよう。
60を素因数分解すると、
60 = 2^2 × 3 × 5
になったよね??
指数が奇数になってるのは、
- 3
- 5
の素因数。
よって、ぜんぶの指数を偶数にするためには、
「60」に「3」と「5」をかければいいね。
そうすると、
2^2 × 3^2 × 5^2
になる。
こいつを2乗でくくってやると、
(2×3×5)^2
になるね!
つまり、
60に自然数15をかけてやると、900になって、
そいつは30の二乗になってるんだ。
今回の例題では、
できるだけ小さい数をかける
って条件があったね。だから、
3×5、つまり、15が答えになるよ。
まとめ:素因数分解の応用問題はけっきょく素因数分解
応用問題の解き方はわかったね。
- 素因数分解する
- 指数が奇数になってる素因数をみつける
- 指数を偶数にするためにかける数を考える
っていう3ステップさ。
慎重にといてみよう!
そんじゃねー
Ken