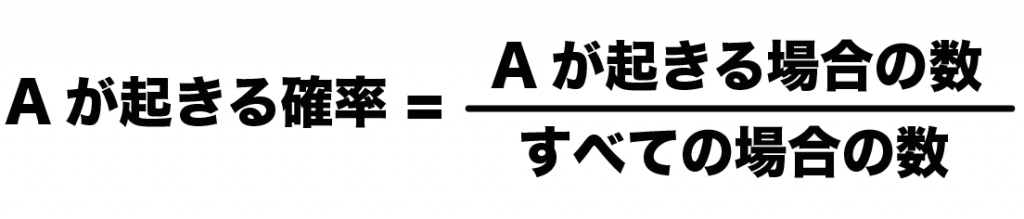【中2数学】確率問題の解き方がわかる5ステップ
確率の問題の解き方がわからない!!
こんにちは!この記事をかいているKenだよ。チャーハンは万能だね。
確率の問題ってむずいよね??
場合の数をかぞえたり、
樹形図をかいてみたり・・・・
なんだろう、
大忙しだ。
っていうか、解き方がよくわからないときが多いはず。
そこで今日は、
中学数学でつかえる確率問題の解き方を5ステップで解説していくよ。
テスト前に参考にしてみてね。
確率の問題の解き方がわかる5ステップ
確率の問題は5ステップでとけるよ。
- 樹形図をかく
- すべての場合の数を調べる
- あることがらの場合の数を調べる
- 確率を公式で計算
- 約分する
つぎの例題で解き方を解説していくね。
例題
A・B・Cの3枚のカードを並べるとき、BとCが隣り合わせになる確率を求めよ。
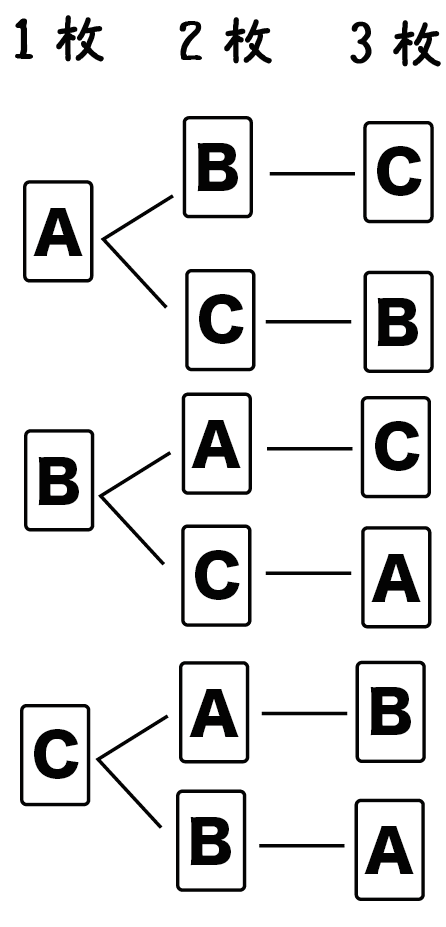
Step1. 樹形図をかく!
まず樹形図をかいてみよう。
中学数学では場合の数を調べる方法は、
樹形図しか、ない。
だから、
めんどいかもだけど樹形図をかいてみよう。
カードA・B・Cの並べ方はつぎのようになるよ。
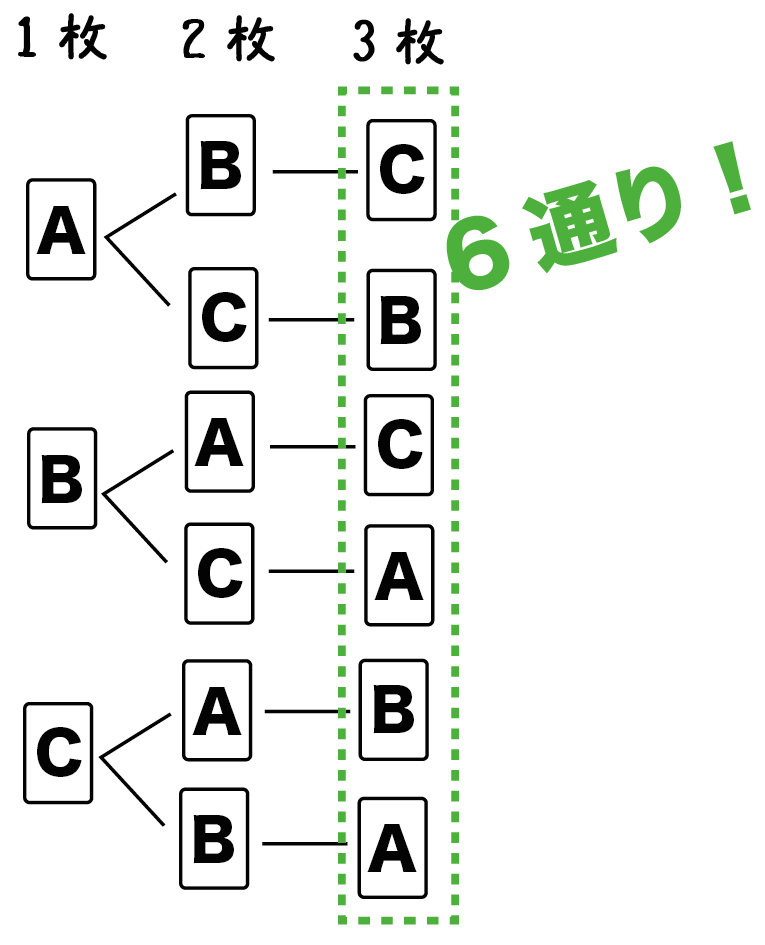
Step2. 「すべての場合の数」を数える!
樹形図から「すべての場合の数」を調べよう。
いちばん右の「実の数」を数えればいいんだ。
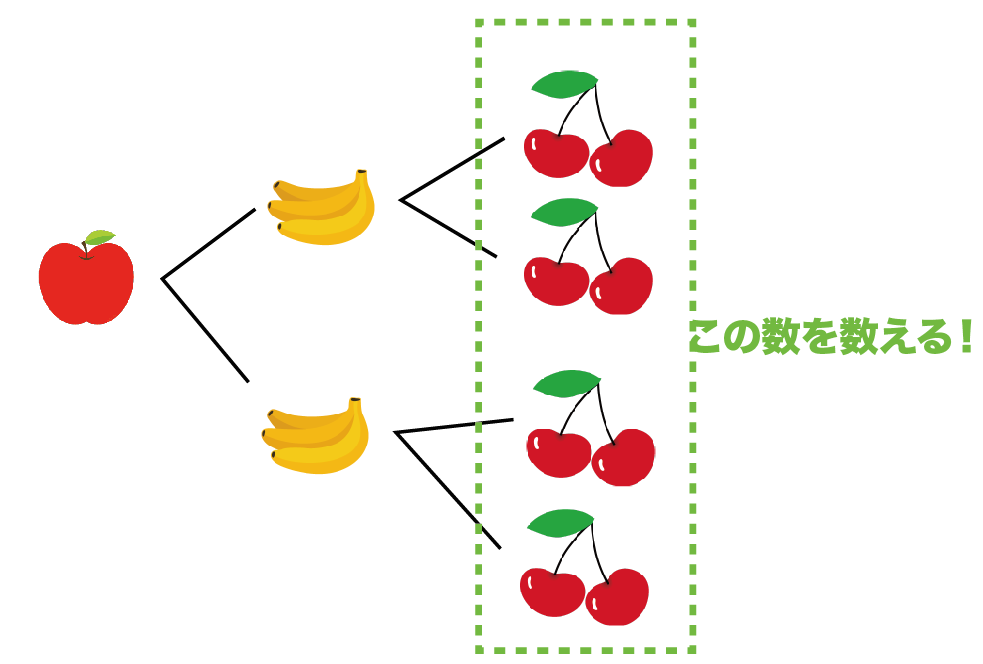
例題の樹形図では「6」だね??
つまり、
すべての場合の数は「6通り」あるってことさ。
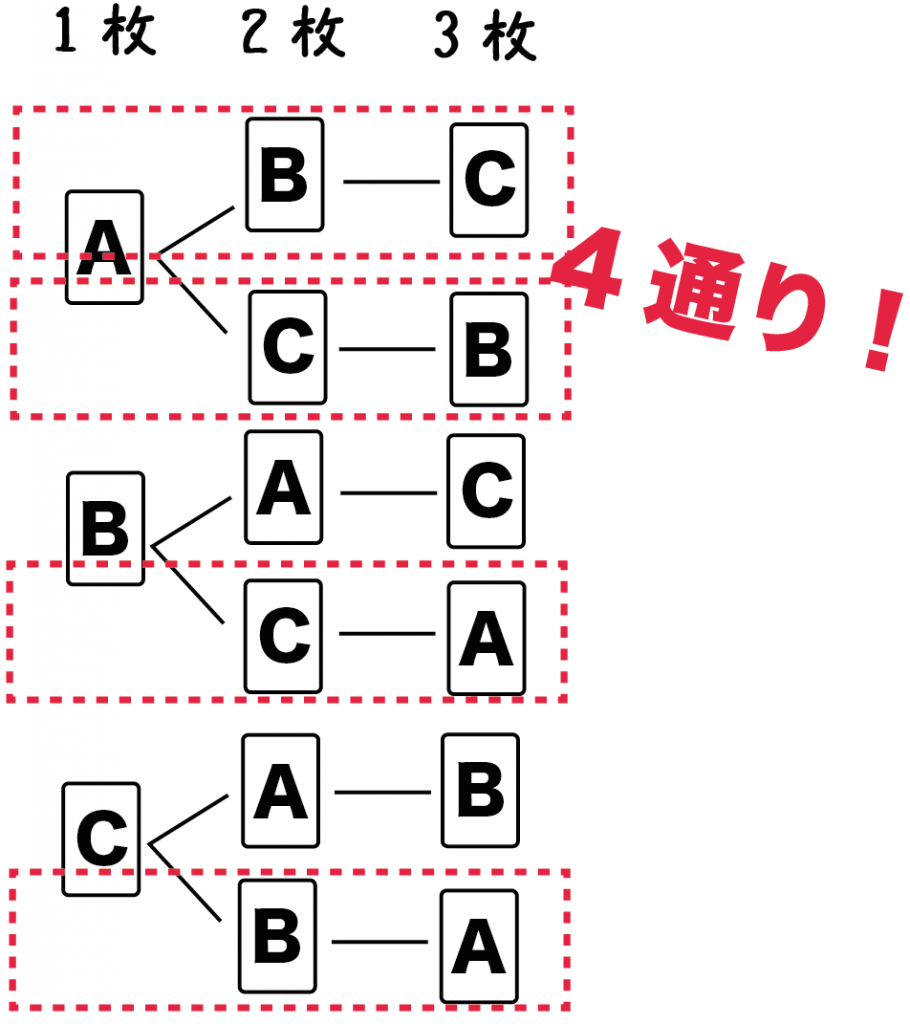
Step3. 「あることがら」の場合の数をしらべる!
「求めたいことがら」の場合の数をしらべよう。
例題でいうと、
BとCが隣り合わせになる場合の数
をしらべればいいんだ。
樹形図をみてみると、
4通りってことがわかるね。
Step4. 公式で確率を計算!
あとは確率の公式で計算するだけ。
あることがらAが起きる確率は、
(Aが起きる場合の確率) = (ことがらAが起きる場合の数)÷(すべての場合の数)
だったよね??
これを使おう。
例題でいうと、
- BとCが隣り合わせになる場合の数:4
- カードの並べ方すべての場合の数:6
だ。
ってことは確率の計算式をつかえば、
(BとCが隣り合わせになる確率)
=(BとCが隣り合わせになる数)/(すべての場合の数)
= 4/6
になるはず。
Step5. 約分する!
最後に約分しよう。
約分しなくても間違えじゃない。
だけど、先生によっては×にされるかもしれない。
約分して分数を簡単にしよう。
例題の確率は、
6分の4
だったよね??
こいつを約分すると、
3分の2になる。
これがきれいな確率の答えだよ。
まとめ:「約分」までが確率の問題の解き方!
帰るまでが遠足
ってよくいうよね。
だけど、確率では、
約分までが確率だよ。
もう一度約分できるか疑ってみよう!
そんじゃねー
Ken