正三角形の面積の求め方の公式ってある？？
こんにちは！この記事をかいているKenだよ。みかんは1日2個までだね。
正三角形の面積には公式がある。
便利でイカすヤツだ。
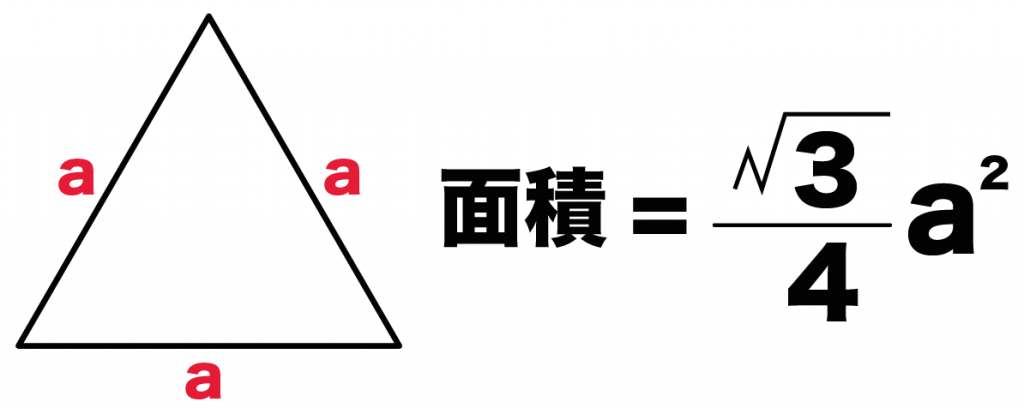
1辺の長さをaとすると面積は、
√3/4 a^2
になるんだ。
つまり、
（正三角形の1辺）×（正三角形の1辺）× √3 ÷ 4
ってことだ。
たとえば、1辺が6cmの正三角形ABCの面積を求めてみよう。
公式をつかって面積を計算すると、
（正三角形の1辺）×（正三角形の1辺）× √3 ÷ 4
= 6× 6× √3 ÷ 4
= 9√3 [cm^2]
になるんだ。
2秒で計算できちゃうね！
正三角形の面積の求め方がわかる3ステップ
がしかし、だ。
公式をおぼえると便利だけど、
忘れた時に悲惨なことになる。
頭真っ白ってやつさ。
今日はそんなときのために、
正三角形の面積の求め方を3ステップで伝授しよう。
例として、
さっきの正三角形ABCの面積を求めていくよ。
Step1. 頂角から二等分線をおろす
頂角の二等分線を底辺にひいてみよう。
頂角が半分になる線をすーーーっと底辺にひけばいいのさ。
例の正三角形ABCでは、
AからBCにむかって二等分線をひけばいいんだ。
んで、
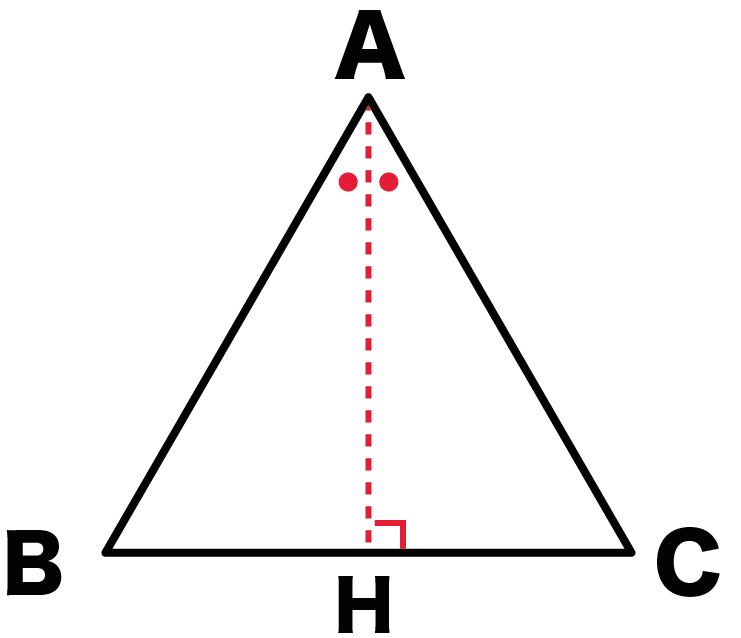
二等分線と底辺の交点をHとしよう。
二等辺三角形の性質の1つに、
頂角の二等分線は底辺を垂直に2等分する
ってものがあったね？
正三角形は二等辺三角形の1種だからこの性質がつかえる。
すると、
AH ⊥ BC
になるよ。
Step2. 高さを比で計算する！
正三角形の高さを計算しよう。
つかうのは、
直角三角形の比
だ。
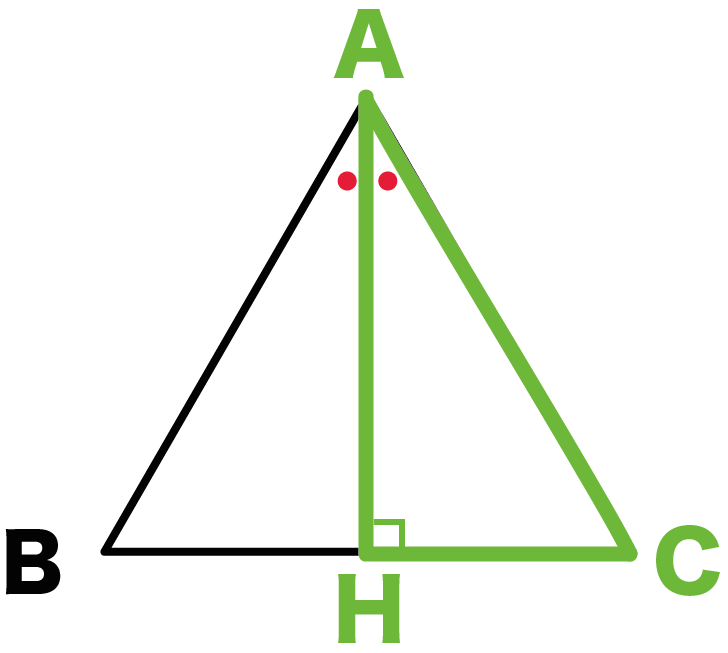
二等分線で半分にわかれた直角三角形に注目して。
例の△ABCでいうと、
△ACHね。
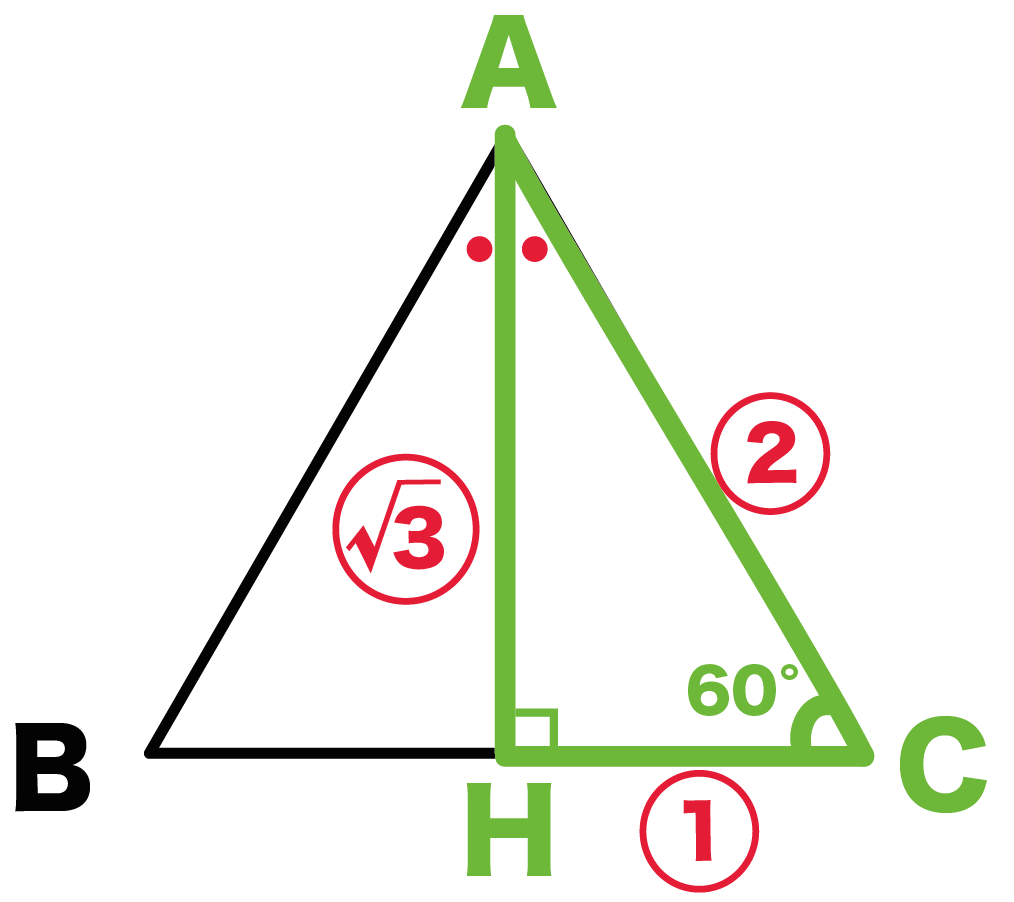
こいつは1つの内角（C）の大きさが60°の直角三角形だね。
だから、各辺の比は、
1: 2: √3
になっているはず。
よって、
高さAH = AC ×√3/2
= 6× √3/2
= 3√3
になるんだ。
メンドイときは正三角形の高さの公式をつかってもいいよ。
Step3. 三角形の面積の公式をつかう！
あとは面積の公式で計算するだけ。
公式って、
底辺×高さ÷2
だったよね？？
三角形ABCでは、
- 高さAH = 3√3 [cm]
- 底辺BC = 6 [cm]
になった。
公式で計算すると、
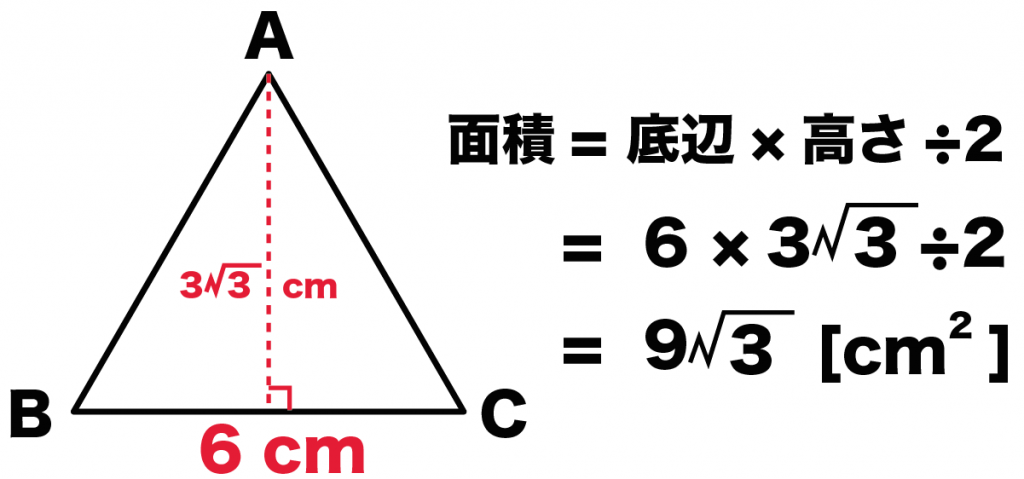
面積 = 底辺 × 高さ ÷ 2
= 6 × 3√3 ÷ 2
= 9√3 [cm^2]
になる。
おめでとう！
正三角形の面積をゲットできねー！
まとめ：正三角形の面積の求め方は暗記するな！
正三角形の面積の求め方には公式がある。
だけれども、
忘れたらテストで即死することになる.
公式の求め方をおぼえておくようにしよう！
そんじゃねー
Ken
