正多角形の内角を4秒で計算できる公式
正多角形の内角を計算したいんだけど??
こんにちは!この記事をかいているKenだよ。映画は1日2本までだね。
正多角形の内角を知りたいときってあるよね??
多角形の内角の和は公式つかえばドヤ顔できるけど、
せ、正多角形の内角はどうすれば・・・??
ってなるよね。
そんな流れで、
正多角形の内角の求め方を解説していくよ。
よかったら参考にしてみてね。
4秒で計算できる!正多角形の内角の公式
正多角形の1つの内角の大きさを求めたいときは、
つぎの公式をつかってみて。
正n角形の1つの内角は、
180°(n-2)/ n
で計算できちゃうって公式だ。
さっそく、正五角形の内角を計算してみよう!
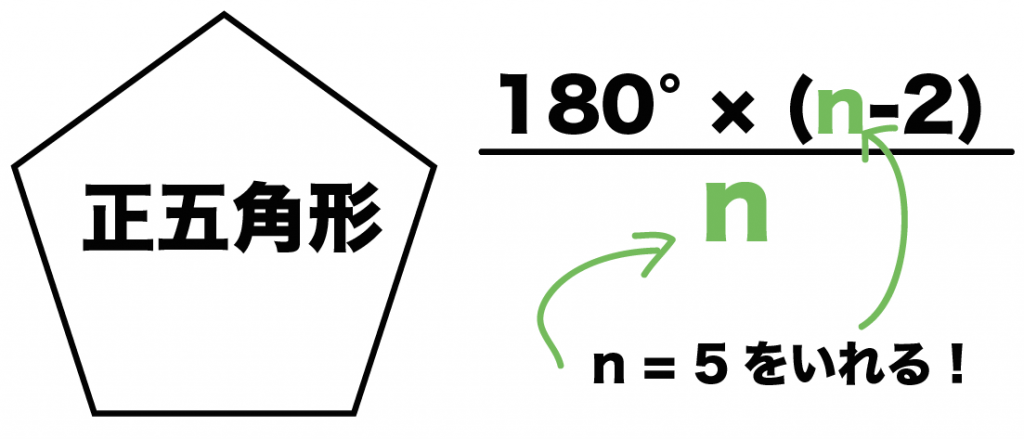
正五角形は頂点が5つあるから、
さっきの公式のnに「5」をいれるだけでいいんだ。
すると、
180 × (n-2)/n
= 180×(5-2)/5
= 108°
になるね。
つまり、
正五角形の内角の大きさは「108°」ってことさ。
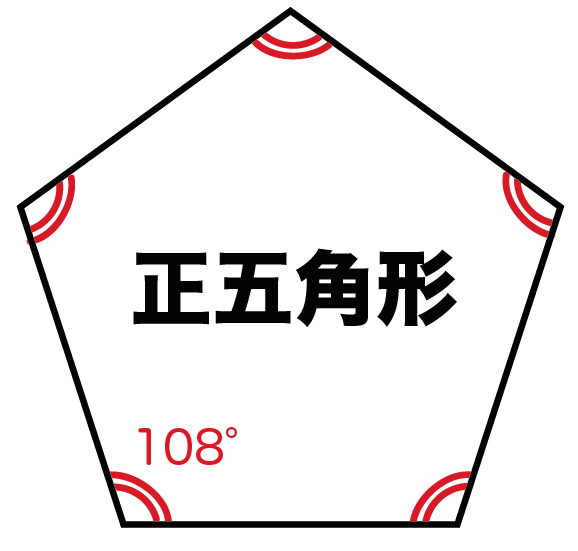
くそ便利でしょ??。
なぜ正多角形の内角が計算できるの??
でもでも、なんで、
180× (n-2)/n
で計算できちゃうんだろう??

都合よすぎるよね?。
なぜそうなるの??
ってことを確認してみよう。
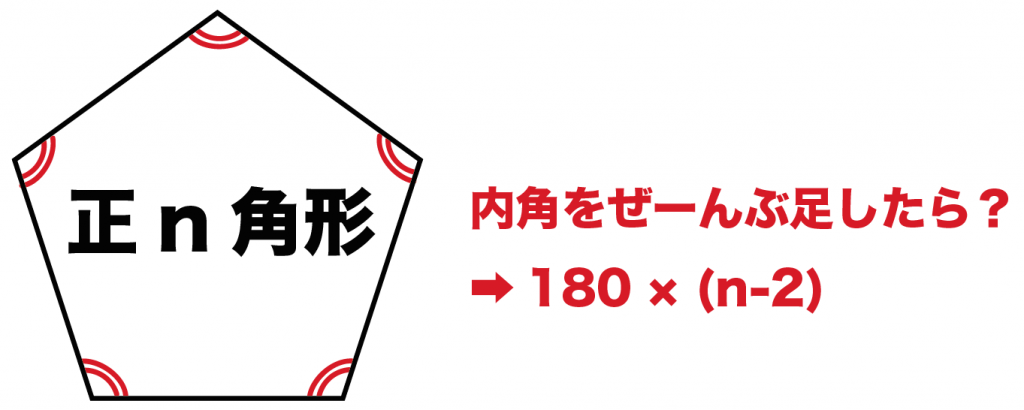
正多角形の内角の和っていくつ??
正多角形の内角をぜーんぶ足したらどうなる??
って考えてみて。
多角形の和の公式を使うと、
正n角形の内角の和は、
180°×(n-2)
になるよね。
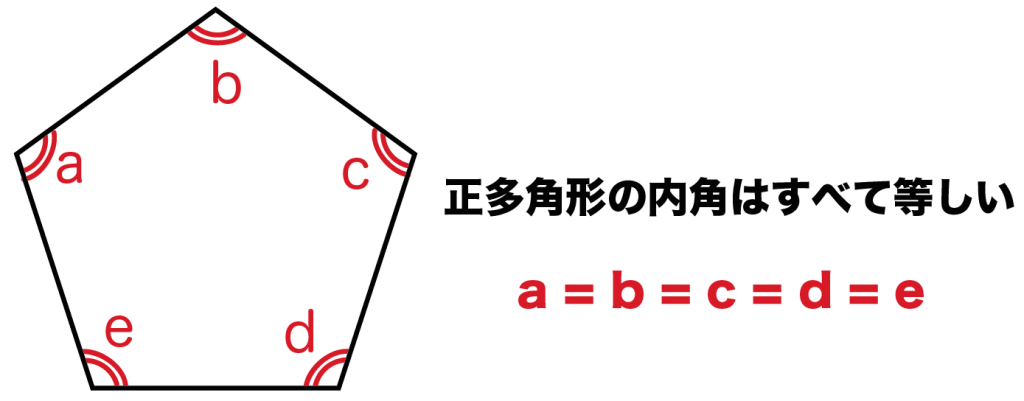
正多角形の特徴は○○である。
正多角形の特徴の1つに、
内角の大きさはすべて等しい
ってものがある。
たとえば正五角形を考えてみよう。
5つの内角を、
- a
- b
- c
- d
- e
とすると、
a = b = c = d = e
になるんだ。
だから、
正多角形の1つの内角の大きさを出したいときは、
内角の和を頂点の数でわればいいんだ。
内角の和「180°×(n-2)」を、
頂点の数「n」でわると正多角形の1つの内角の大きさになるよ。
180× (n-2)/n

どの内角も同じ大きさだからね!
まとめ:正多角形の内角は「総和」を「頂点の数」でわれ!
正多角形の内角の公式は、
180°×(n-2)/n
だったね。
ようは、
「内角の和」を「頂点の数」でわればいいんだね。
よくでる問題だからテスト前に復習してみてね。
そんじゃねー
Ken