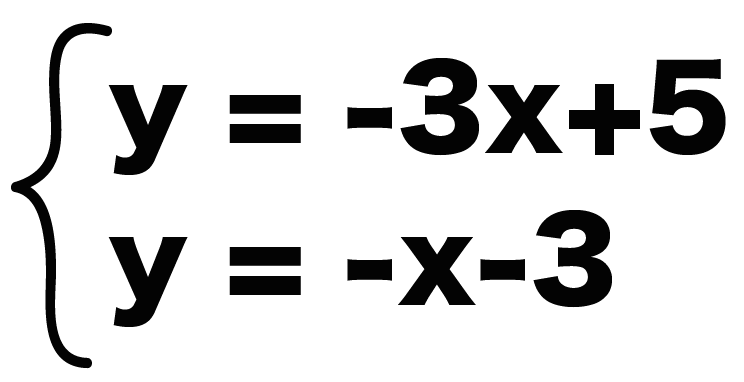2直線の交点の座標の求め方？？
こんにちは！この記事をかいているKenだよ。うどん食い過ぎたね。
一次関数の問題に、
2直線の交点の座標を求める問題
ってやつがある。
たとえば、つぎのようなヤツね↓↓
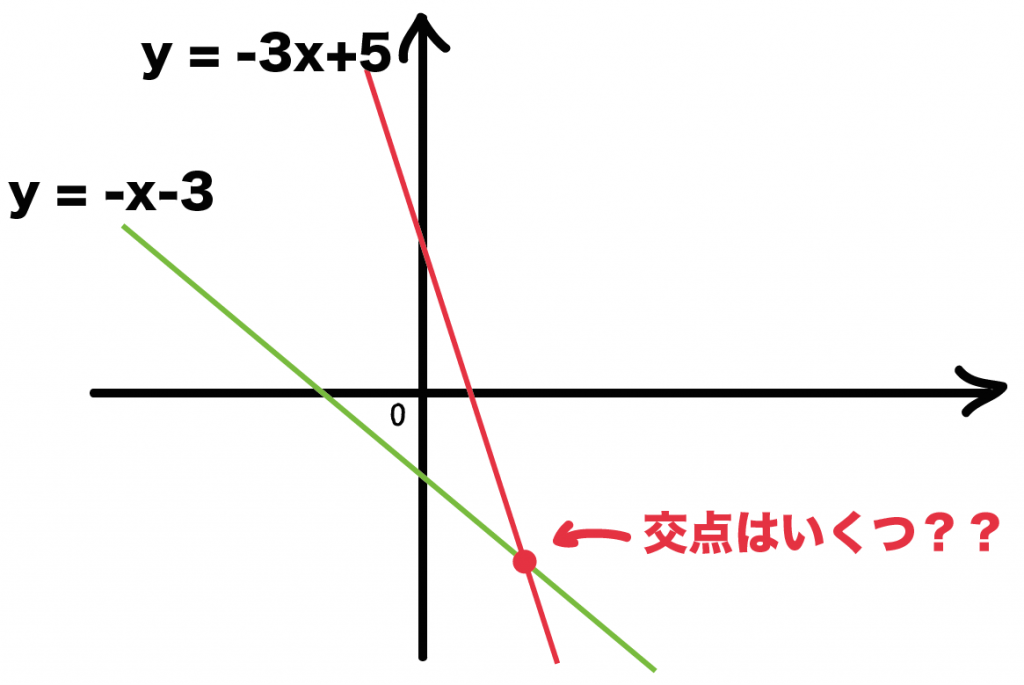
直線 y = -x -3と y = -3x + 5の交点の座標を求めなさい。
このタイプの問題はゼッタイ期末テストにでる。
うん、ぼくが先生だったら出したいね。うん。
今日はこの問題をさくっととけるように、
二直線の交点の求め方を解説していくよ。
2直線の交点の座標の求め方がわかる3ステップ
まずは基本をおさらいしよう。
連立方程式とグラフの記事で、
方程式をグラフにすると、
「2直線の交点」が「連立方程式の解」になっている
って勉強したよね？
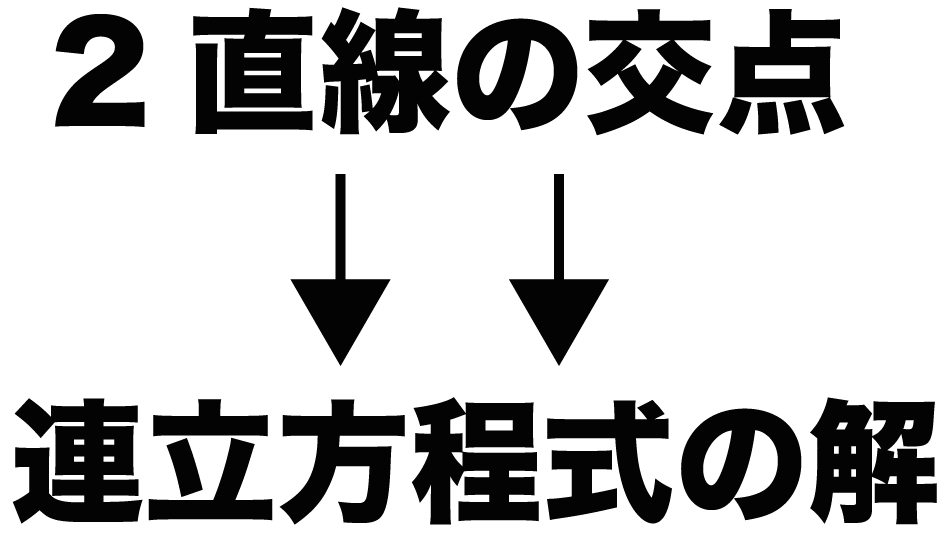
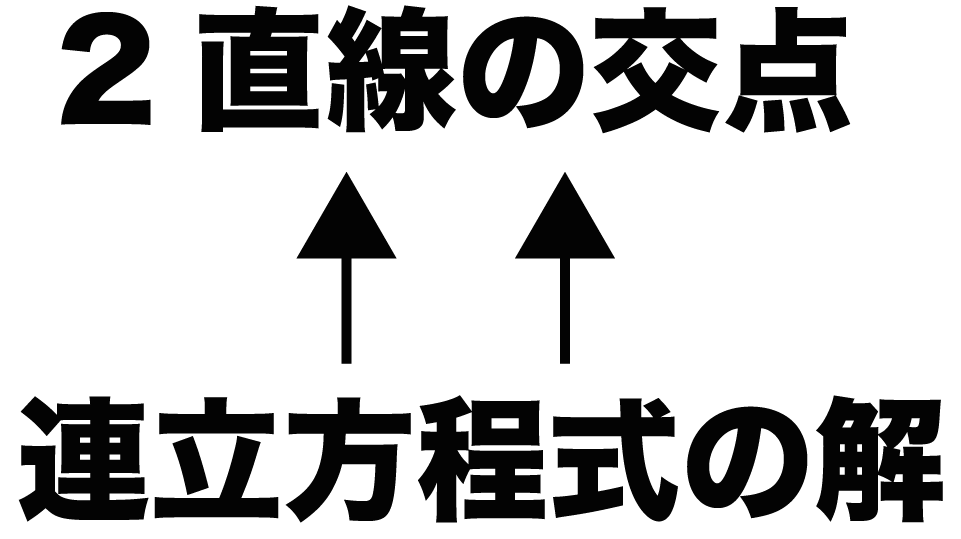
今回はこれを逆手にとって、
「連立方程式の解」を計算して「交点の座標」を求める
ということをするよ。
例題をときながら勉強していこう。
直線 y = -x -3と y = -3x + 5の交点の座標を求めなさい。
つぎの3ステップでとけちゃうよ。
Step1. 連立方程式をたてる
2直線で連立方程式をたてよう。
「方程式の解」が「交点の座標」になるはず！
例題の直線は「y = -x -3」と「y = -3x + 5」だったね。
こいつらを連立方程式にしてやると、
y = -x -3
y = -3x + 5
になるでしょ？
2つの一次関数をタテに並べてみてね。
Step2. 文字をけす！
1つの文字の方程式にすれば、
一次方程式の解き方で計算するだけでいいんだ。
例題では連立方程式の左辺が「y」で2つとも同じだね。
だから、
代入法をつかったほうが早そう。
上の式にyを代入してやると、
-x – 3 = -3x + 5
2x = 8
x = 4
になる。
これでxの解が求まったわけだ。
Step3. 解を代入する
最後に「解」を「直線の式」に代入してみよう。
例題でいうと、
ゲットした「x = 4」を、
y = -x -3
y = -3x + 5
のどっちかに代入すればいいんだ。
とりあえず、xの係数が1の「y = -x -3」に「x = 4」を代入してみよう。
すると、
y = -x -3
y = -4 -3
y = -7
になる。
2直線の連立方程式の解は「直線の交点の座標」だったね？
ってことは、
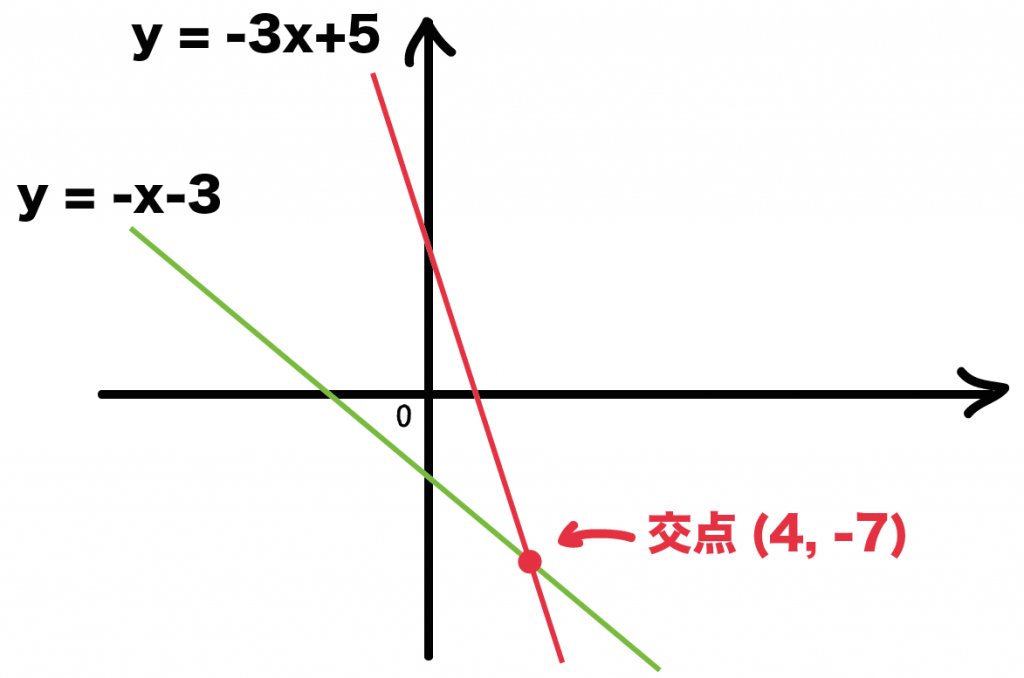
この2直線の交点の座標は、
（x, y ）= (4, -7)
になるってことさ。
おめでとう！
これで二直線の交点の求め方をマスターしたね。
まとめ：2直線の交点は連立方程式の解である
2直線の交点・・・？ しらねえよ・・・・
ってなったとき。
連立方程式をたてて、それを解けばいいんだ。
そのxとyが交点の座標になるよ。
連立方程式の解き方を忘れたときはよーく復習してみてね！
そんじゃねー
Ken
