【一次関数】直線の式がわかる4つの求め方
1次関数の直線の式の求め方がわからない??
こんにちは!この記事をかいているKenだよ。洗濯物ためすぎたね。
一次関数の式を求める問題
ってけっこうあるよね。下手したら、3問に1問ぐらいは出るかもしれない。
テスト前におさえておきたい問題だね。

今日はこの「直線の式を求める問題」をわかりやすく解説していくよ。
よかったら参考にしてみてね^-^
一次関数の直線の式がわかる3つの求め方
まず、直線の式が計算できるケースを確認しよう。
つぎの4つの要素のうち、2つの値がわかっているときに式が求められるんだ。
- 傾き(変化の割合)
- 切片
- 直線が通る座標1
- 直線が通る座標2
たとえば、傾きと切片がわかっているとき、とか、座標と切片がわかっているとき、みたいな感じだね。

求め方のパターンをみていこう!
パターン1. 「傾き」と「切片」がわかっている場合
まずは一次関数の「傾き」と「切片」の値がわかっている場合だ。
たとえば、つぎのような問題だね。
例題
yはxの一次関数で、そのグフラの傾きは-5、切片は7であるとき、この一次関数の式を求めなさい。
このタイプの問題はチョー簡単。
一次関数の式「y = ax + b」に傾き「a」と切片「b」の値を代入するだけだよ。
例題での「傾き」と「切片」は、
- 傾き: -5
- 切片:7
だね。
だから、一次関数の直線の式は、
y = -5x + 7
になる。
代入すればいいだけだから簡単だね。
パターン2. 「傾き」と「座標」がわかってる場合
つぎは「傾き」と「座標」がわかっている場合だ。
たとえばつぎのような問題だね。
例題
yはxの一次関数で、そのグラフが点(2, 10)を通り、傾き3の直線であるとき、この一次関数の式を求めなさい。
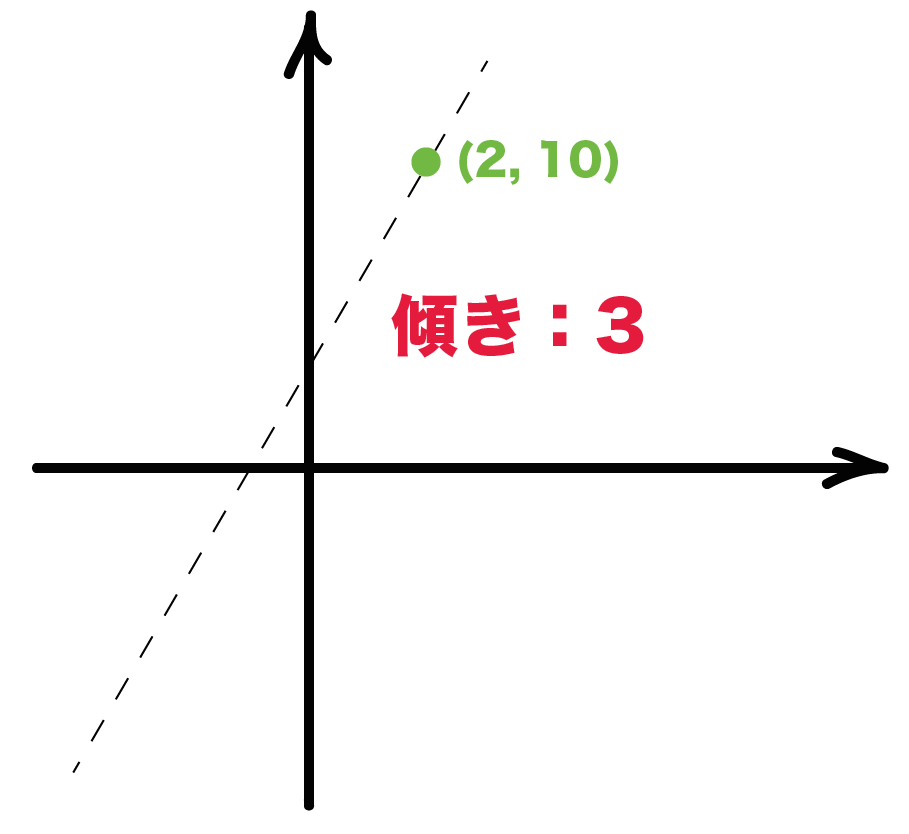
この手の問題も同じだよ。
一次関数の式「y = ax + b」に傾きaと、座標を代入してやればいいんだ。
bの方程式ができるから、そいつを根性でとくだけさ。
例題では、
- 傾き:3
- 座標(2, 10)
っていう一次関数だったよね??
まずはaに傾き「3」を代入してみると、
y = 3x +b
になるでしょ? そんで、こいつにx座標「2」とy座標「10」をいれてやればいいのさ。
すると、
10 = 3 × 2 + b
b = 4
になるね。
つまり、この一次関数の式は「y = 3x + 4」になるよ!
こんな感じで、傾きと座標をじゃんじゃん代入していこう!。
パターン3. 「切片」と「座標」がわかっている場合
つぎは「切片」と「座標」がわかっている問題だね。

たとえば、つぎみたいなヤツさ↓↓
例題
yはxの一次関数で、そのグラフが点(2, 11)を通り、切片3の直線であるとき、この一次関数の式を求めなさい。
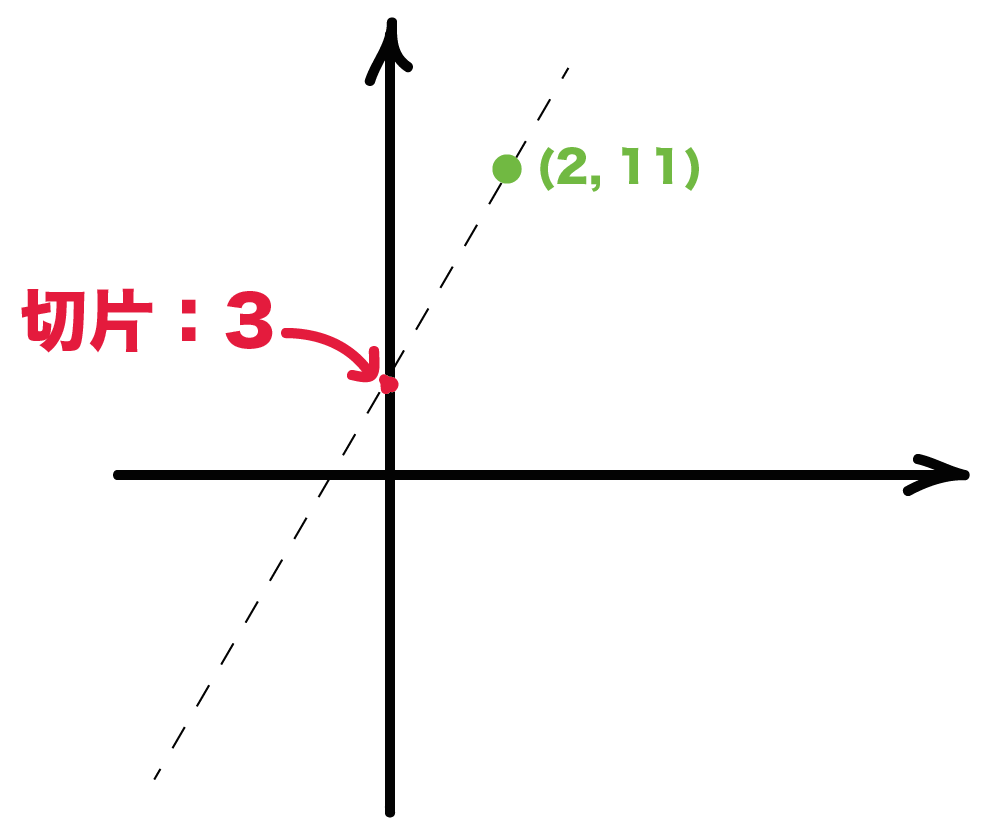
このタイプの問題もいっしょ。
一次関数の式「y = ax +b」に切片と座標を代入してやればいいんだ。
そんで、できた方程式を解いてやれば直線の式が求められるね。
例題では、
- 切片:3
- 座標(2, 11)
だったね?
切片の「3」をy = ax+bに代入してみると、
y = ax + 3
になるね。
そんでコイツに、
- x座標「2」
- y座標「11」
を代入してやると、
11 = 2a + 3
になる。
この方程式をaについて解いてやると、
11 = 2a + 3
2a = 8
a = 4
になる。
つまり、この一次関数の傾きは「4」ってことだ。
だから、
一次関数の式は「y = 4x + 3」になるね。
このタイプの問題も代入して方程式をとくだけさ!
パターン4. 直線を通る2点がわかっている場合
最後は、直線が通る2点の座標がわかっている問題だ。
たとえば、つぎのような問題さ。
例題
つぎの一次関数の式を求めなさい。
グラフが、2点(1, 3)、(-5, -9)を通る直線である。
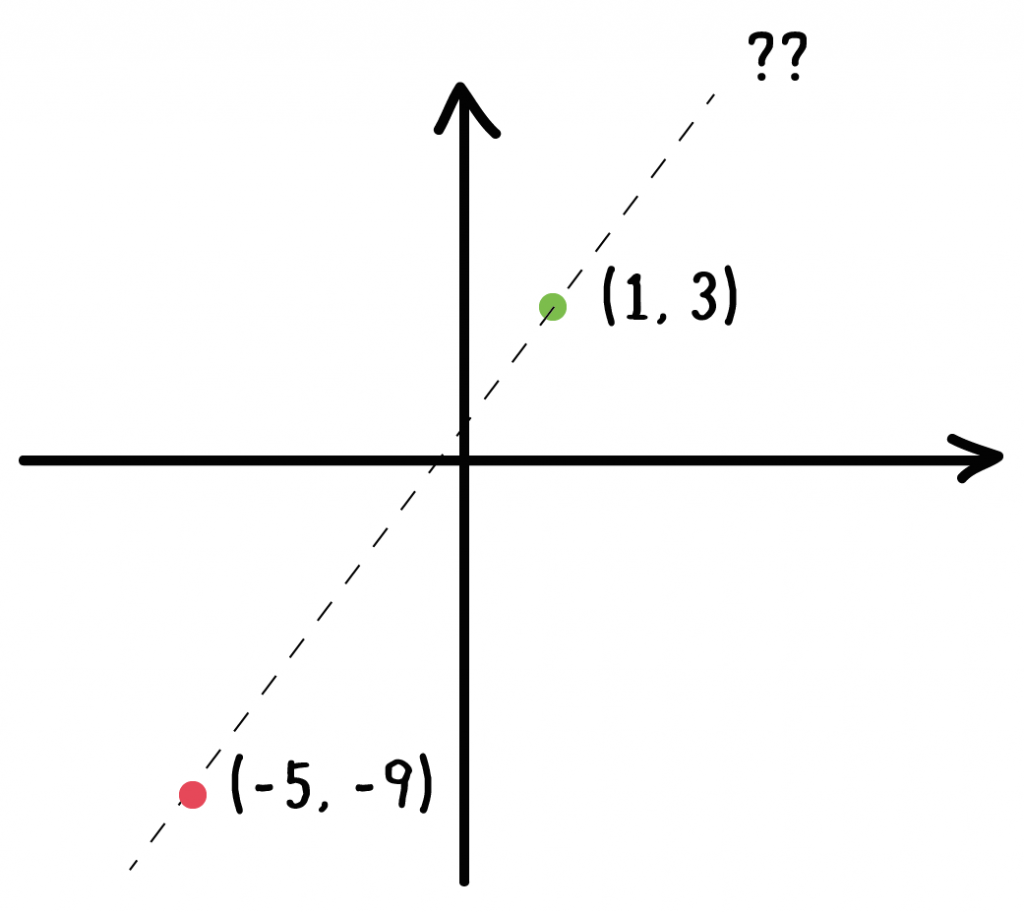
ちょっとめんどくなるけど、解き方はこれまでと一緒。
一次関数の式「y = ax + b」に2点の「x座標・y座標」を代入してやればいいのさ。
問題に慣れるまで練習してみてね。
まとめ:直線の式を求める問題は4パターンで攻略できる!
直線の式を求め方はどうだった??
4パターンあるとか言っちゃったけど、
だいたいどれも解き方は一緒。
一次関数の式「y = ax + b 」に、
- 傾き
- 切片
- 座標
のうち2つを代入してやればいいんだ。
テスト前によーく復習してね。
そんじゃねー
Ken





