【光の屈折】コインが浮かび上がって見える作図問題の解き方
コップにコインを入れて水を入れるとコインが浮かび上がる??
こんにちは!この記事を書いているKenだよ。麦茶、冷えてるね。
中1理科では「光の屈折」という光の性質を勉強してきた。
光の屈折の法則とは簡単にいうと、
光がある透明な物体を通過すると、光の道筋が曲がる
というものだったね。
>>詳しくは「光の屈折」を参照
この光の屈折の効果を確認できる実験として、よく、
コップにコインを入れて、水を注ぐと浮かび上がって見える
というものが実施されるね。
どういう実験か具体的に見ていこう。
まず、何も入ってないからのコップがあるとしよう。
こいつにコインをチャリーンと入れる。
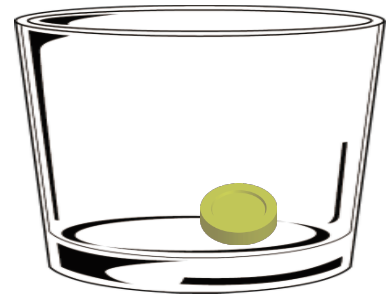
この状態だと、コップのふちに隠れて外からはコインが見えないはず。
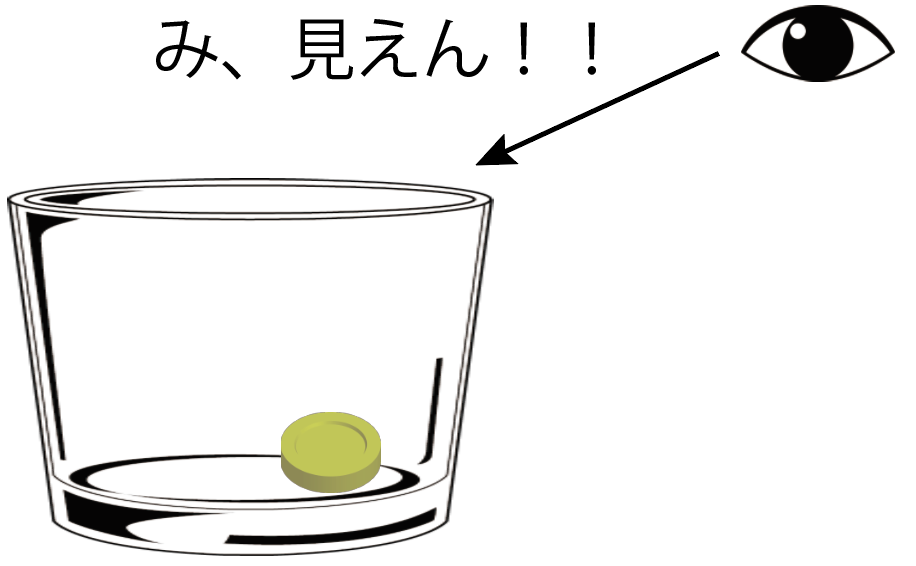
ここで、コップに水をドボドボ注いでみよう。
すると、どうだろう??
さっきまで見えなかったコインが浮き出て見えるようになってるじゃないか!
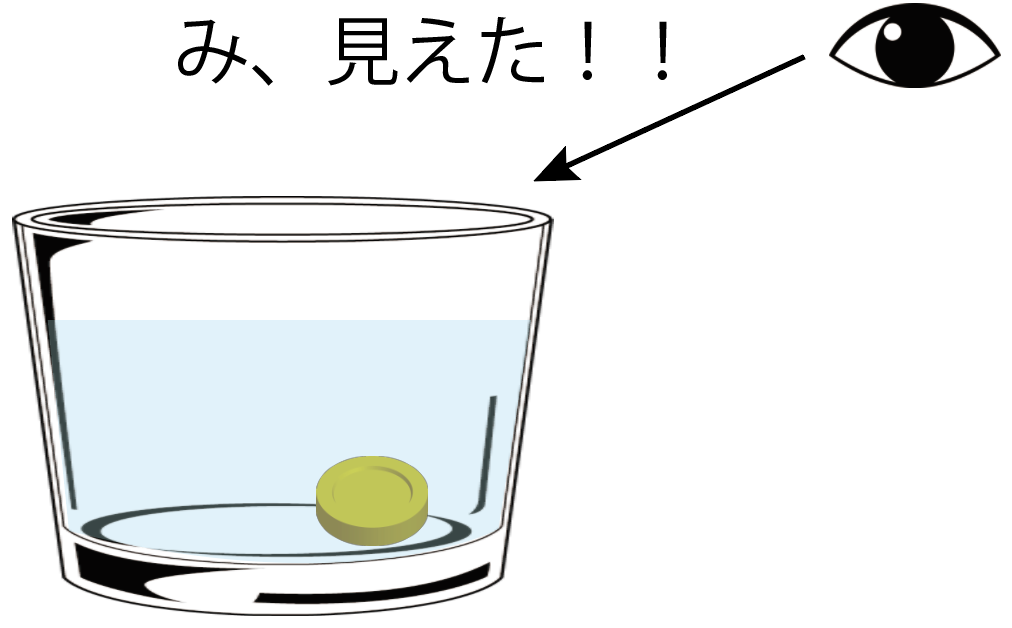
実際にリアルの世界でも実験してみても、やっぱり浮かび上がって見える。
こ、これはどういうことなんだ?!
なぜ、光の屈折でコインが浮かび上がって見えるのか??
それじゃあ、なんで水を入れた途端にコインが浮かび上がって見えるんだろうね??
じつはその理由は、
光の屈折の法則
にあるんだ。
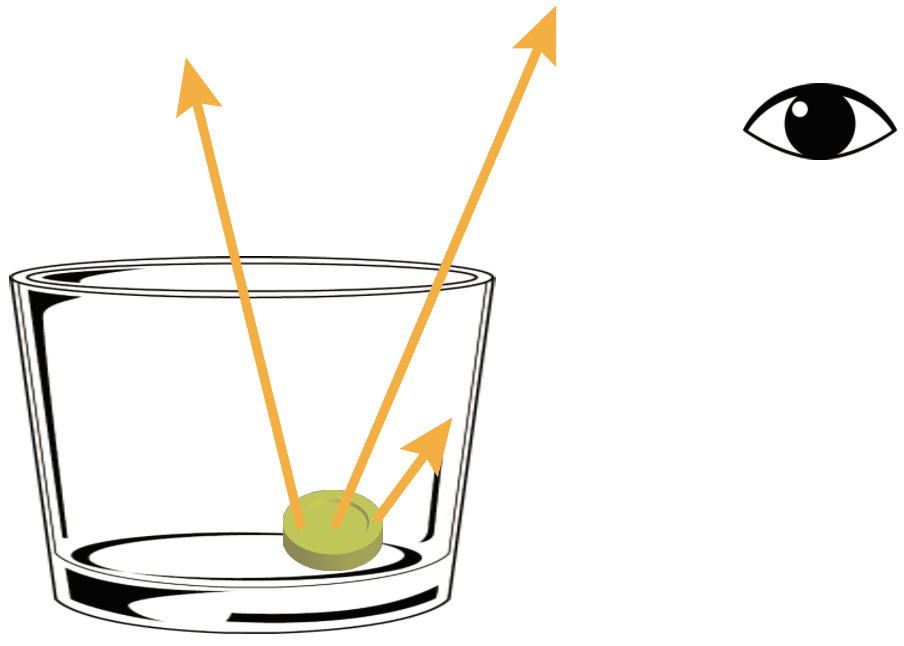
水を入れないと、このコインからの光が目に届かない。
光が目に届かないと、目がコインが見えたっていう指令を脳に送らないから、結果的にいくら踏ん張っても見えないまま。
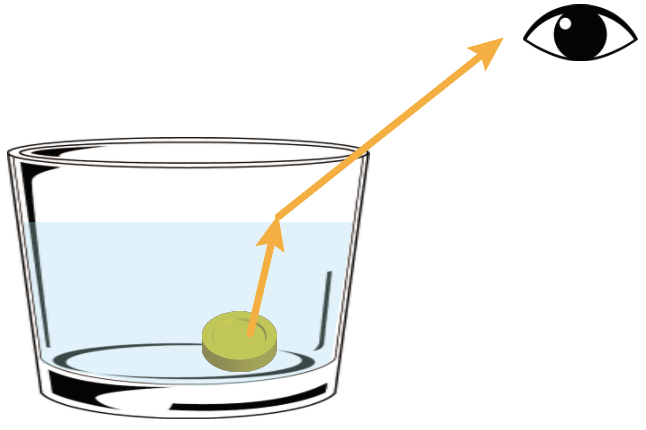
水を入れると、コインからの反射した光が屈折して、無事に目に届くようになるんだ。
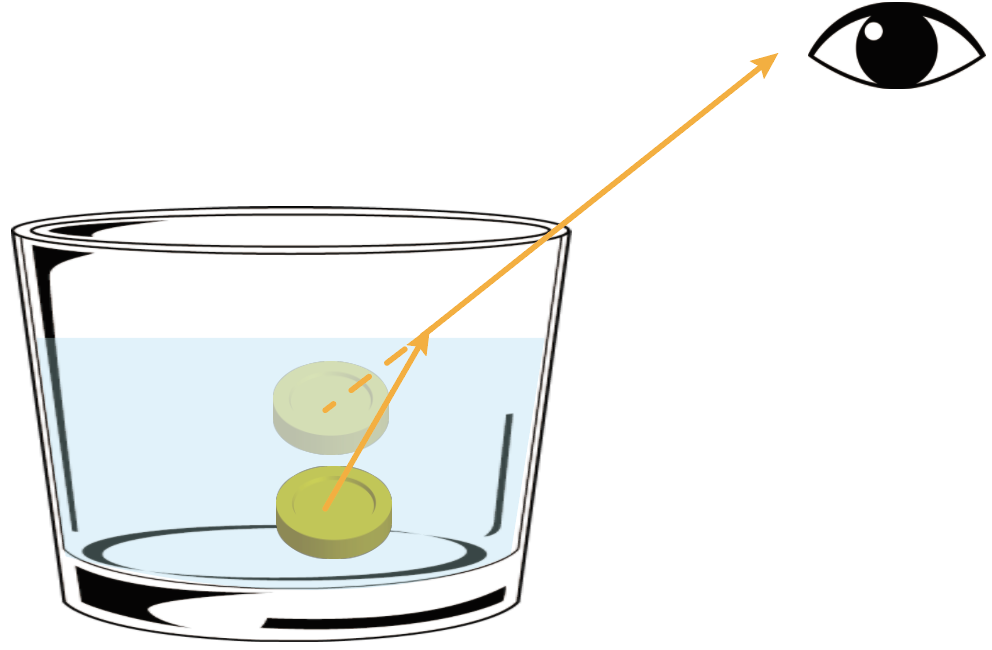
だから、コインは実際の位置ではなくて、目からすると、屈折した光の延長上に見えることになるってわけ。
光の屈折の法則さまさまだ。
光の屈折の法則を使ったコインの作図問題を解いてみよう!
じつは、このコインが浮かび上がる実験はテストでも狙われやすいんだよ。
たとえば、次のような作図問題がよく出題されるかな。
水が入ったコップにコインを入れると浮かび上がって見えた。
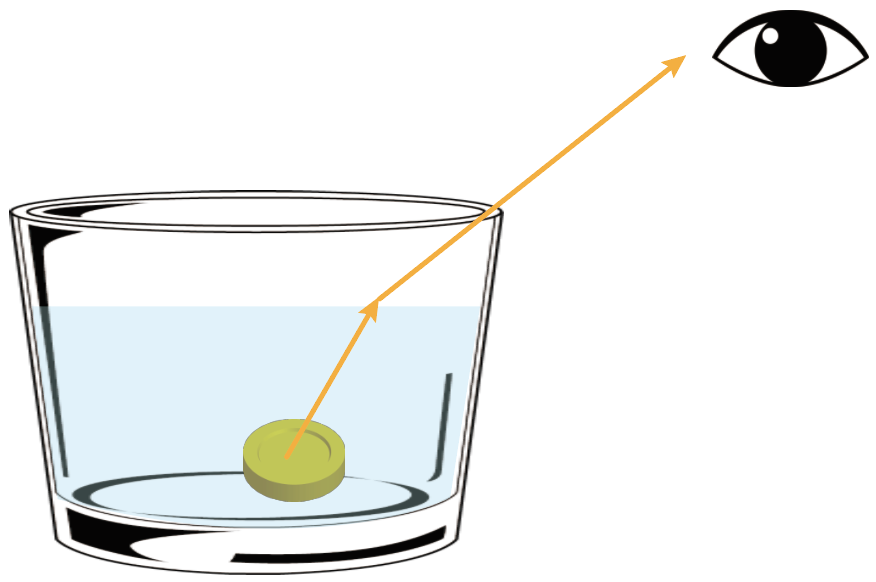
コインの中央からの光が図のように屈折して目に入る時、コインが浮かび上がって見える位置を作図してください。
という問題。
こういう問題では、屈折した光の道筋を逆方向にまっすぐ延長させればいいんだ。
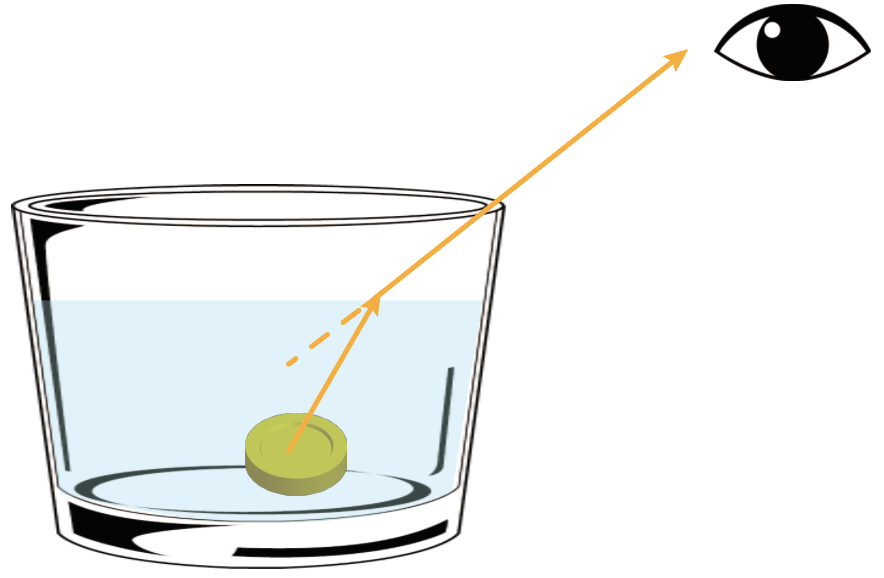
まっすぐ延長線をかくために定規を使ってやろう。
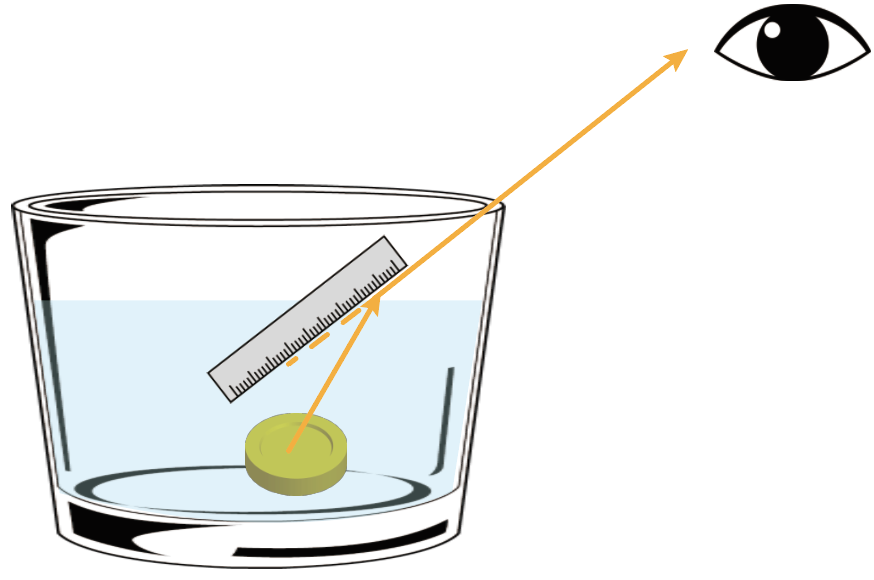
その延長線上にコインが見えているはずだから、だいたい元のコインの位置の真上にコインを作図してやればオッケー。

この手の問題はよくテストに出るから復習しておこう!
そんじゃねー
Ken



