3分でわかる!「整数の集合」と「自然数の集合」の違い
整数の集合?自然数の集合って何よ!?
中学1年生の「正の数・負の数」の単元に、
- 整数の集合
- 自然数の集合
という意味のわからない数学用語が2つ登場します。数学を勉強したての中学1年生にとって、
はあア?整数の集合??え?どこのゲーセンに集合するんだって??
自然数の集合?? あ、おれの地元は自然の集合だからね、なんちゃって
という感じで「整数の集合」や「自然数の集合」の意味がわからなすぎて数学が嫌いになってしまいそうです。これでは日本の数学勉強人口がぐんぐん減ってしまいます。これはいけすかない!

そこで今日は「整数の集合」と「自然数の集合」という数学用語を理解できる記事を書いてみました。その名も、
3分でわかる!「整数の集合」と「自然数の集合」の違い
数学が好きでない中学生の方でも3分でわかるように書いてみました。「正の数・負の数」の単元でつまづきそうになった中学生の方は参考にしてみてください。
「整数の集合」の「集合」ってなに??
「整数の集合」と「自然数の集合の違い」を確認する前に、
集合とは何者か?!?
ということを解説しましょう。
数学の「集合」って何??
オンライン大百科Wikipediaで「集合(set)」の意味を調べてみると、
「もの」からなる「集まり」である
とあります。ものの集まり?? なんじゃそりゃ!ってなりますよね。
ぼくは個人的に「集合」の意味をつぎのように捉えています。
集合とはグループのようなもの
です。えっ。Wikipediaよりわかりづらいですって?!? そうですね、理解をふかめるために具体例をだしてみます。
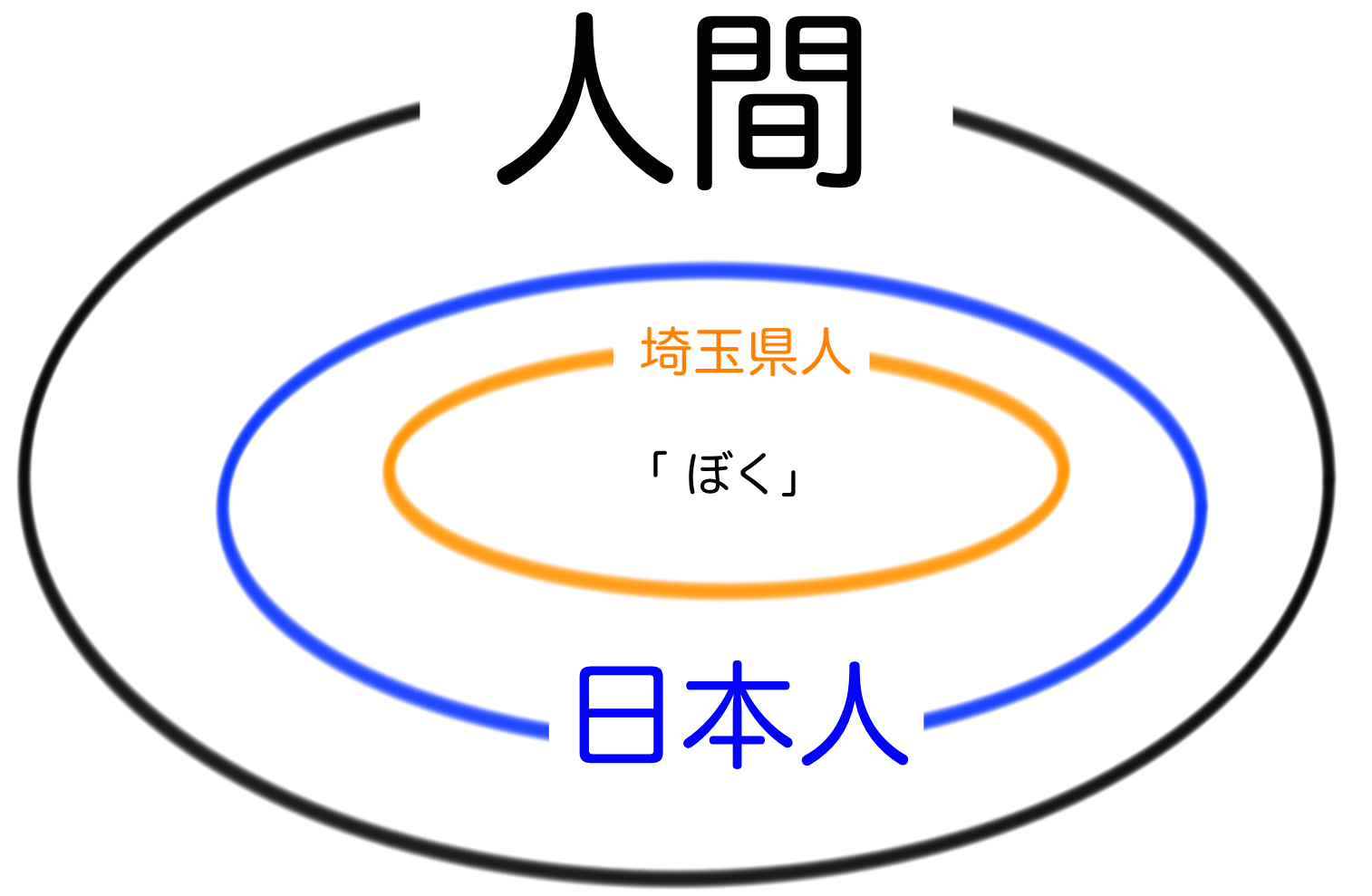
たとえば、「自分」という1人の人間を考えてみてください。ぼくは日本人で埼玉県に住んでいるおにいさんです。この「ぼく」という人間は以下の3つのグループ(集合)に属していることがわかります。
- 日本人
- 埼玉県人
- 人間
これらが集合の良い例です。
つまり、集合に属する「もの」は集合内で似たような性質を持っているのです。
先の「日本人」という集合では「日本に住んでいる、もしくは生まれ育った人間」だけが「日本人」という集合に属することができるのです。なんか人種問題に発展しそうなのでここら辺に言及をとどめておきましょう。
集合には大小関係がある??
集合には大小関係があります。小さい集合もあれば巨大な集合もあるというわけです。
それじゃあ、
- 日本人
- 埼玉県人
- 人間
という3つの集合で一番大きなものはどれでしょうか?? こ、答えは、CMのあとで・・・・・
<<CM>>
答えは、
人間という集合
です。人間には日本人もアメリカ人も含まれます。さらに、埼玉県人や神奈川県人は日本人に含まれます。つまり図で表すと次のようになります。
数学で集合が登場したときにはこのように、
どの集合がどの集合に属するのか??
ということを見極めることが大切です。人間というグループの中に日本人がいる。日本人というグループの中に埼玉県人がいる。といった具合にです。
「整数の集合」と「自然数の集合」って何??
集合の意味を何となく理解できましたか!?
つぎは中学1年生の数学教科書で登場した「整数の集合」と「自然数の集合」について考えてみましょう。
集合とはグループのことでしたね??
つまり整数の集合とは
整数の数のグループのこと
です。自然数の集合も同様に、
自然数の数のグループのこと
です。
「整数の集合」と「自然数の集合」はどっちが大きい??
人間、日本人、埼玉県人、という集合のときと同様に、
「整数の集合」と「自然数の集合」のどちらが大きいか考えてみましょう!!
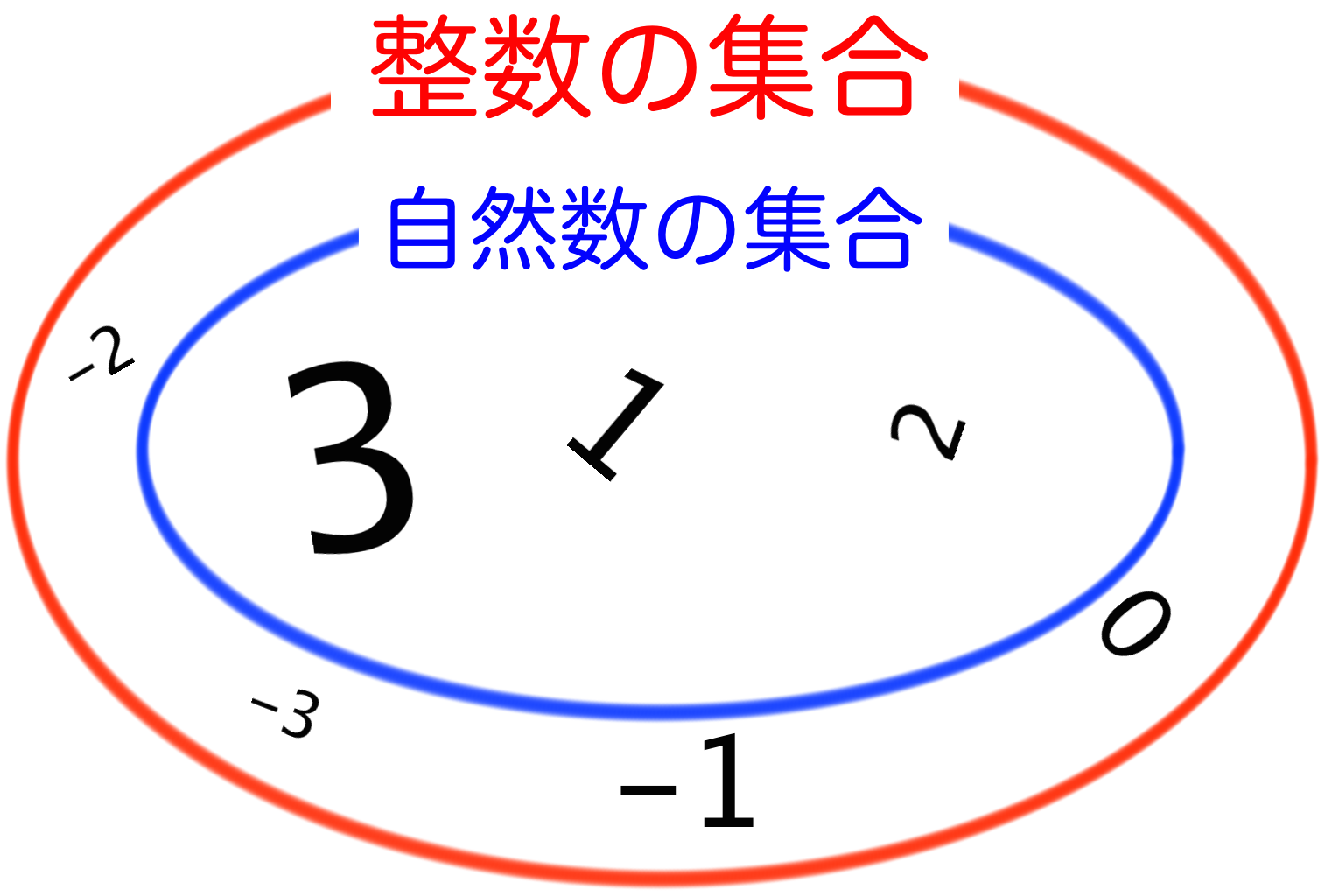
整数とは…-3, -2, -1, 0, 1, 2, 3…..でしたね? 自然数とは指で数えられる数1, 2, 3, 4, 5…..です!
数直線で考えてみると次のようになります。
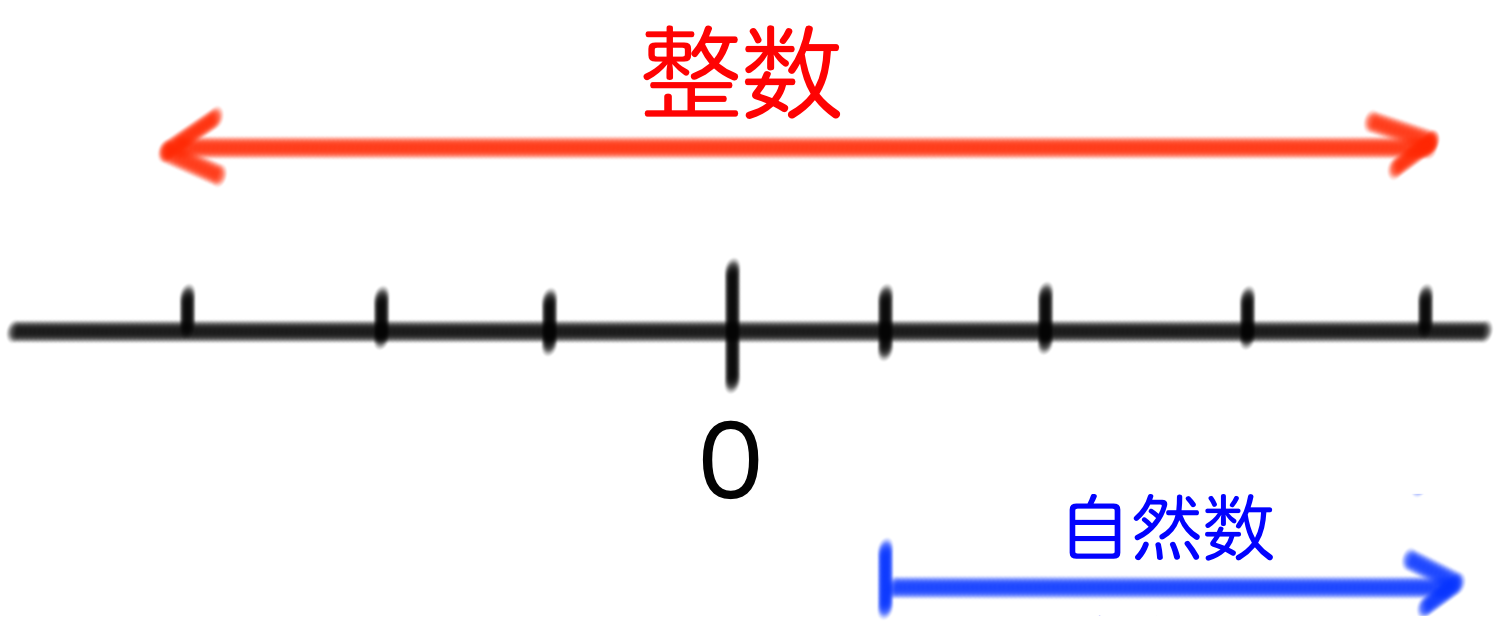
この数直線から視覚的にわかるのは、
「自然数の集合」が「整数の集合」に含まれている
ということです。1という数は自然数でもあり整数でもあります。2も3も同様。
がしかし、-1や0といった数はどうでしょう??これらは整数ですが自然数ではありません。つまり、整数の集合のほうが自然数の集合より守備範囲が広いんです。
この2つの集合の関係を図にあらわすと次のようになります。
数学の集合では、
どっちの集合がデカいのか!?
という疑問をなげかけることが大切。頭でじっと考えてもわからないときは上のような絵を描いてみましょう!
「整数の集合」と「自然数の集合」よりも大きな集合は??
じつは整数の集合よりも大きな数の集合があります。
それは「数全体の集合」というヤツです。これはいったいどういうことなんでしょうか!???
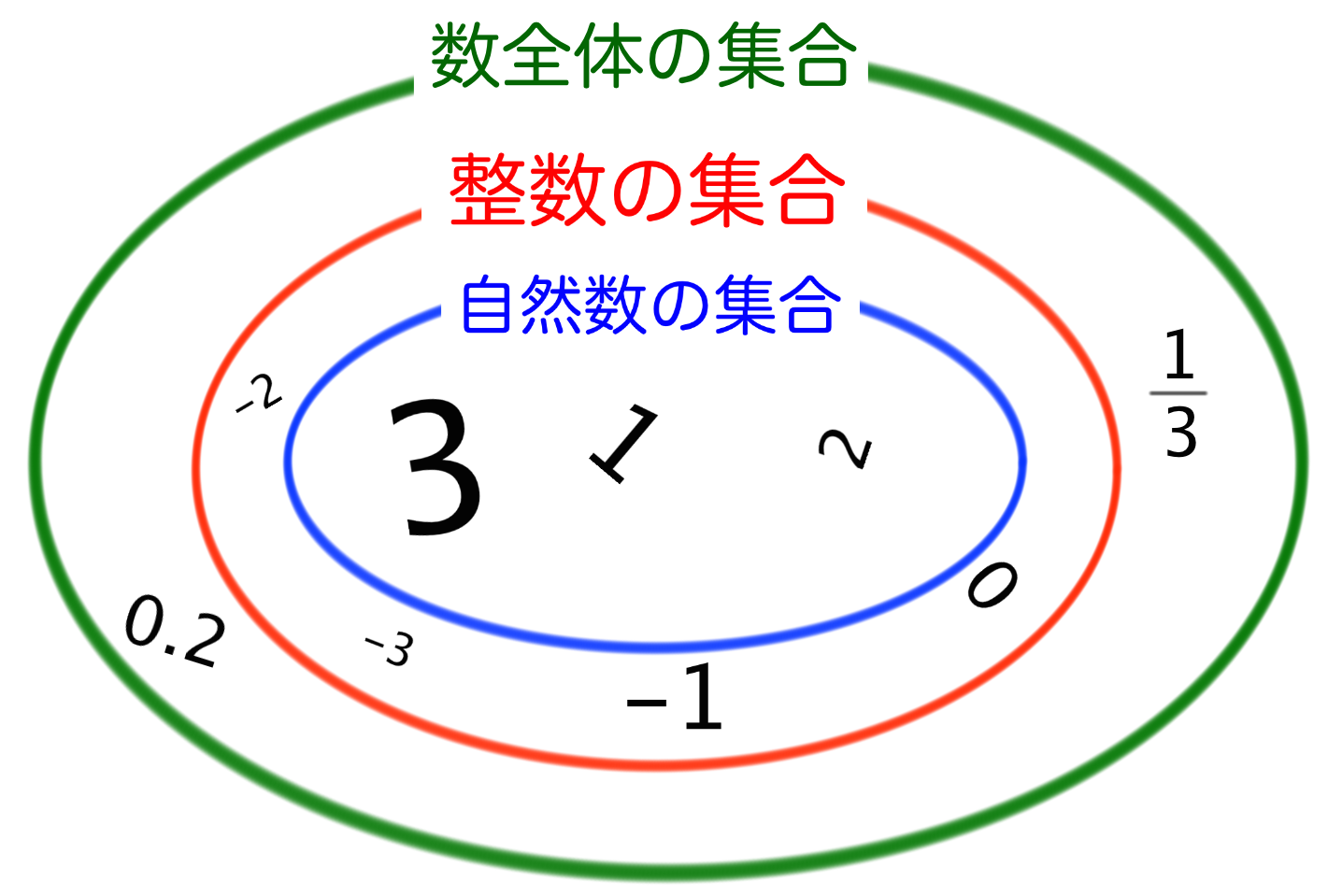
ご存知の通り、整数には分数、小数・・・といった中学数学で登場する数が含まれません。たとえば0.2、といった数たちですね。
これらは中学数学では「数全体」という集合で表現されます。なぜなら、数字なら何でも「数全体」という集合に属することができるからです。
「数全体」「整数」「自然数」という3つの数の集合の関係をさきほどのように図で表現すると、
という感じになります。
「整数の集合」「自然数の集合」よりも大きな「数全体の集合」を忘れないであげてくださいね!。
もしかしたらテストにひょっこり出題されるかもしれません。
「整数の集合」と「自然数の集合」の違いOKですね!
ここまでスピーディーに「整数の集合」と「自然数の集合」の違いを確認してきました。
中学数学で「数の集合」の問題が出題されたら、
どちらの集合がより大きいのか
ということを確認してみましょう。どんな難しい問題でも瞬殺できるはずです。
それでは、また今度です!
Ken