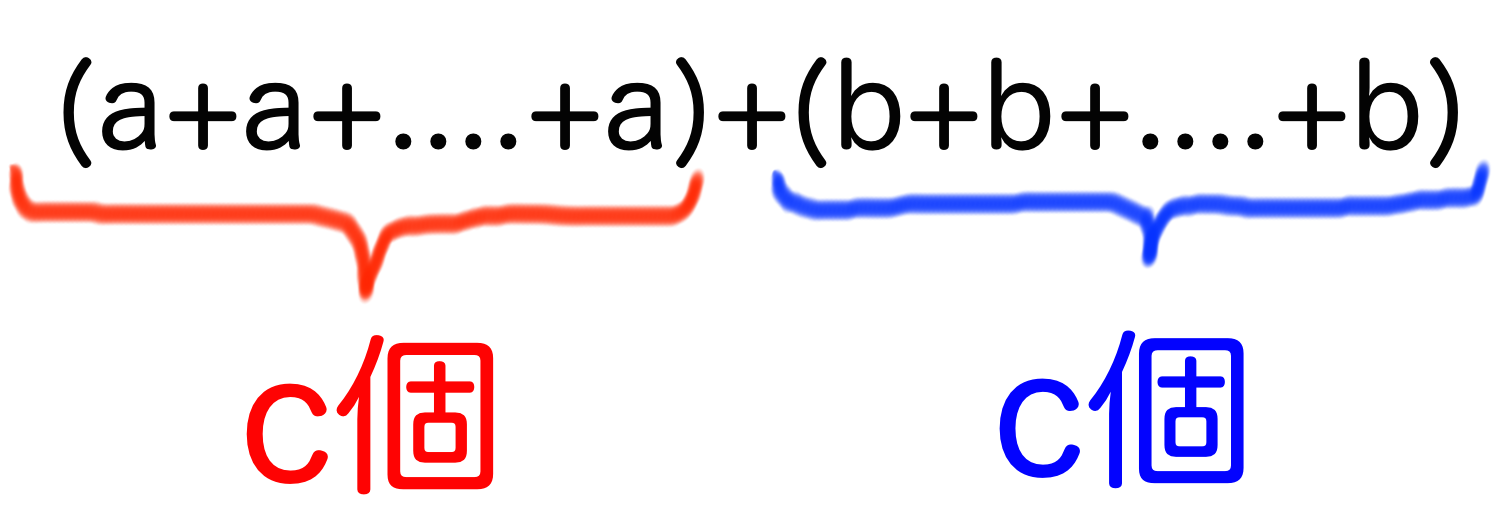5分で理解できる！分配法則の証明

分配法則の証明を5分ぐらいで理解したい！

中学数学でもっとも頻繁に利用する計算法則。それは、

分配法則（distributive property）

というものです。「分配法則のチョー便利な1つの使い方」という記事でもお伝えしましたが、もう一度「分配法則」を復習してみましょう。分配法則とは次のような計算法則でした。

a, b, cという3つの数があったとすると、
$(a+b)\times c=a\times c + b\times c$

分配法則のことをちまたでは「カッコをはずす法則」と呼んでいます。

()を含んだ複雑な計算式も分配法則を使えばイチコロ。1発か2発でカッコなしの計算式に直せるのです。

これは便利ですよね？？　分配法則は3年間を通して頻繁に登場します。がっちり押さえておきましょう！

ところが、です。ところが。

なぜ分配法則は成立するのでしょうか？？

たしかに分配法則は超便利な計算法則。だがしかし、分配法則が使える理由を考えずに乱用していては数学が得意になりません。

たとえるなら、野球のルールを知らずにバットを振り回しているようなもんです。今日は、そんな便利な分配法則の証明をわかりやすく解説してみました。

分配法則がなぜ使えるのか証明したい！！

そんなアツい志をもった方に参考にしてほしいですね。

分配法則の証明をするため、さきほどの $(a+b)\times c=a\times c + b\times c$ という計算式を例にとりましょう。数学が苦手な方でも理解できるように3ステップで分配法則を証明してきますねー。

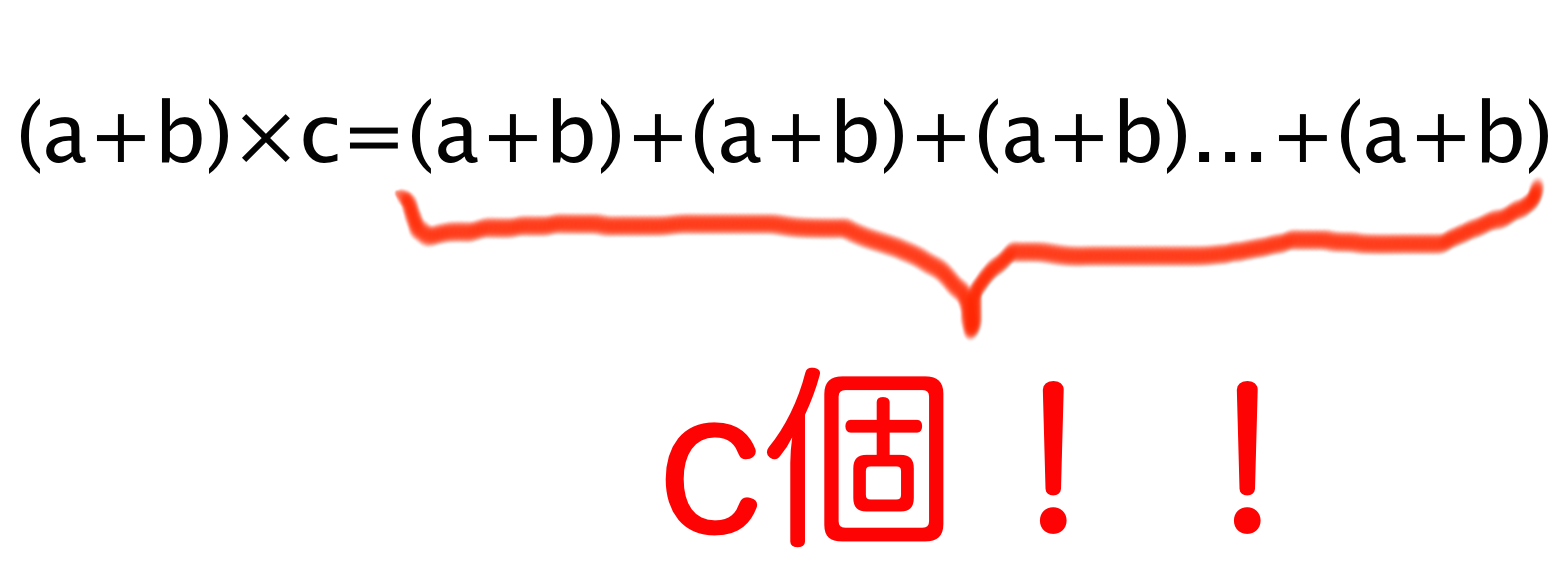
$(a+b)\times c$ という計算式の意味をまず振り返ってみましょう。これは、

$(a+b)$ という数のセットを $c$ 回たし合わせたもの

でしたよね？？　図で表すとつぎのようになります。

次は同じ英文字ごとに足し合わせてみましょう。aはa、bはbという感じです。この状態ではカッコの外に数字がかけられていないので()を自由に取り外せますね！

すると、aがc個、bもc個たし合わされていることに気づきます！だって、(a+b)のセットがもともとc個ありましたからね。ハンバーガーとポテトのセットが2つあったらハンバーガーが2個、ポテトも2個あるのと同じです。

最後にもう一度「掛け算」の意味を振り返ってみます。

掛け算とは、

ある同じ数のセットを繰り返し足し合わせたもの

でしたね？？　この掛け算の意味を考慮すれば、

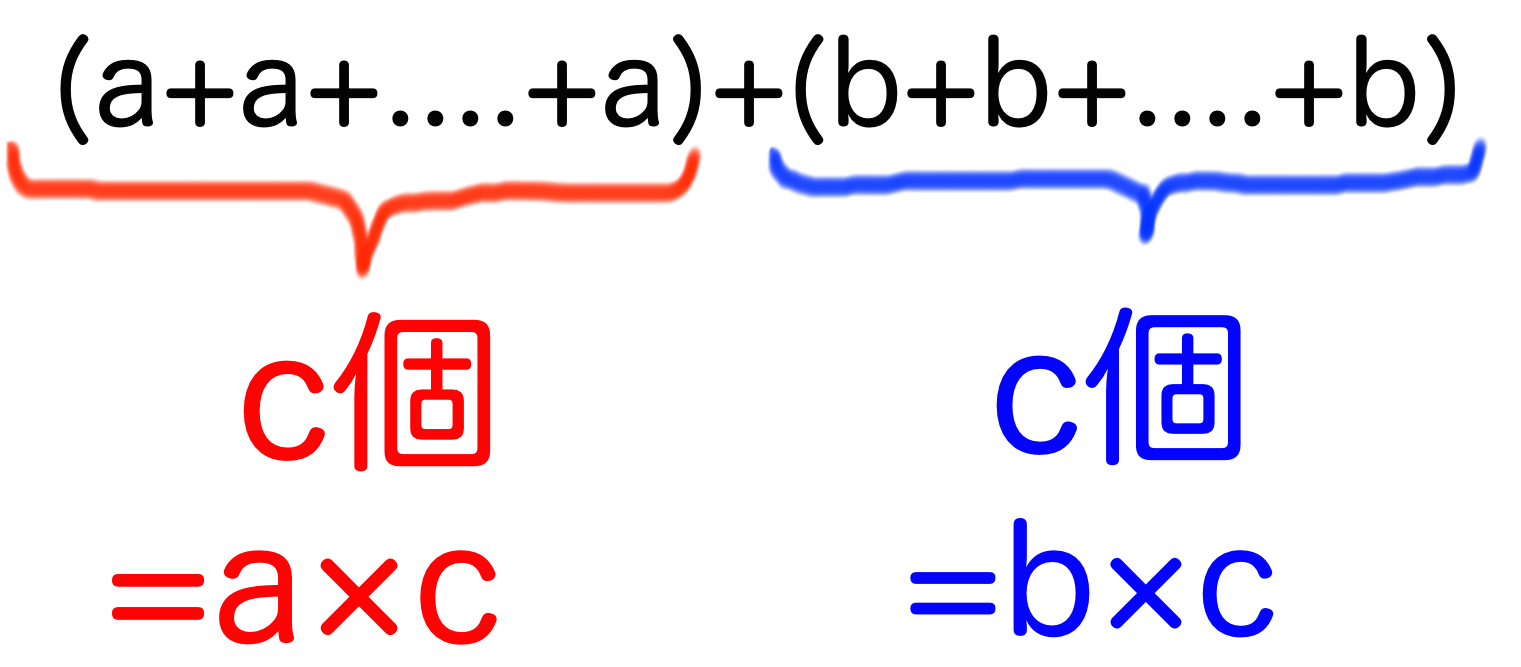
「aをc個足し合わせた数」= $a\times c$

「bをc個足し合わせた数」= $b\times c$

と掛け算に書き直すことができるのです。

この3ステップを経てようやく、

$(a+b)\times c=a\times c + b\times c$

といえるわけですね！分配法則が証明できてよかったよかった！

一番はじめに5分で分配法則を証明することを目標としていました。

さて実際、どうだったでしょうか？？？　ものの3分、いや35秒ぐらいで分配法則を証明できちゃいましたね。

中学数学の教科書には分配法則の証明はのっていません。

だがしかし、自分の頭をつかってみて、

なぜ分配法則がいえるのか？？

と考えて証明してみることが大切。数学を今後も勉強していく上で「なぜ？なぜ？？」という問いをしながらすすめてみてください。

それでは！また今度です。

Ken