交換法則と結合法則の違いがよくわからない！？？
中学数学の最初の単元「正の数・負の数」で2つの計算法則が登場します。
それは、
交換法則 (commutative property)と結合法則(associative property)
です。数学を勉強しはじめた中学生のたちは、
交換？ 結合？？ 法則とかうさんくせえー
なんて不平をもらし、数学を嫌いになってしまうかもしれません。
数学が嫌いになりそうになったので、Wikipediaで結合法則の意味を調べてみると、
数学、殊に代数学における結合法則（けつごうほうそく、英: associative law) 、結合則、結合律あるいは演算の結合性（けつごうせい、英:associativity）は二項演算に対して考えられる性質の一つ。ひとつの数式中で演算が一度よりも多く行われるとき、その演算を評価する順番に関わらず結果が同じになるような演算は結合的 (英: associative) であるといわれる。
と書いてあります。余計に意味不明で泣きそうになりますよね、コレ。
そこで今日は数学を勉強し始めた中学生の方でもよくわかるように、
交換法則と結合法則の使い方
を説明します。交換法則とか結合法則の意味がわからなすぎて泣きそうになっている！？？
そんなときに参考にしてくださると嬉しいです。
中学数学で勉強する「交換法則」とは何か？？？
まずは最初に「交換法則」の正体を暴いていきます。交換法則とはずばり、
計算式に含まれる項の順序を入れ替えていいよ！
という法則です。したがって、項の数が2つ以上の計算式から「交換法則」を適用できるわけです。たし算（加法）とかけ算（乗法）の2つの場合に適応できることが知られています。
たとえば、
という計算式があったとしましょう。この文字式に交換法則をあてがってやると、
という具合に計算順序をかえてもいいんです。これは加法の場合の交換法則です。教科書では俗に「加法の交換法則」と呼ばれています。
えっ。乗法の交換法則の例もみてみたいですって！？？
そうですね、先ほどの足し算の記号＋を×に直して、
という計算式をつくってやれば、乗法の交換法則の出来上がりです。
計算式の項の順序をいれかえても加法・乗法の計算結果は変わらない
という法則が交換法則です。わかりやすいですよね！？？
それじゃあ、「結合法則」って何よ？？
それでは、もう一つの計算法則である「結合法則」とはいったい何者なのでしょうか。
先ほどWikipediaでの結合法則の意味を確認してみましたね。ただ、あの定義は難しすぎて数学を猛烈に勉強した人にしかわかりません。
そこで改めてここで「結合法則」を再定義してやると、
3つ以上項がある計算式で、どのペアーから計算しても構わないYO!!
というものです。この「結合法則」は「交換法則」と同様に「たし算とかけ算」の2つの場合に適応することができます。
し、しかも項の数が3つ以上？？ なんだかうさんくさい数学の法則ですね。具体例といっしょに理解を深めてみましょう。
たとえば、
という計算式があったとします。3つも項があるので厄介な計算式です。
ふつうに何も考えずに計算すると、まず
つまり、
のように無意識に前の2つの項を()でくくっています。
ただ、
そこで登場するのが「結合法則」です。結合法則を適応してやると、
という計算式の
を先に計算したっていいことになります。つまり、
のように後ろ2つの項をくくっても良い訳です。
この計算をすると、
そして、この20という数値に第一項の9をかけて、
という計算をすることになります。これは先ほどのという計算式と比べるとかなり楽勝になっています。だって、20ってきりのいい数字ですからね。そろばんを習ってなくても答えは、
と導くことができます。一見、複雑な計算式をカンタンにできる。これこそが結合法則の武器です。
先ほど紹介したのは「乗法の交換法則」です。かけ算の場合ですね。この結合法則は足し算（加法）の場合にも適応できます。足し算の計算式でも臆せずじゃんじゃん使って行きましょう。
交換法則と結合法則を合わせると何が生まれるのか？？
それじゃあ、ここまで勉強した「交換法則」と「結合法則」を抱き合わせるとどんなことが分かるのでしょうか？？
じつは交換法則と結合法則から、
加法・乗法の計算式では、どの項から計算してもいいし、どの項同士をくっつけてもいい
ということが言えます。つまり、自分が計算しやすいように項を自由に動かしていいのです。かつてフランス革命によりフランス国民に自由が与えられたように、「交換法則と結合法則」によって中学生に計算の自由が与えられたわけです。
ただし、ここで1つ注意点があります。
加法と乗法（たし算とかけ算）が混じった計算式では、
カッコ内の計算→乗法→加法
という計算順序があります。十分に注意して取り組みましょう。
交換法則と結合法則を応用して計算問題を瞬殺してみよう！
最後に実際に「交換法則」と「結合法則」を利用して計算問題をといてみましょう。
計算問題1.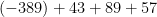 
見た目がかなりごっつく厳つい顔をしています。交換法則と結合法則を使わなかったら返り討ちをくらいそうな勢いです。
このモンスターを退治するために、さっそくモンスターを倒してみましょう。
どうやらこの式を眺めていると、
をしてしまえば、89という端数が消えて計算がカンタンに成りそうな気がします。しかも、残りの2つの項だって足せば丁度いい数になりそうな気がします。そこで、まず交換法則を用いて、
という具合に計算順序を入れ替えます。次に、結合法則により、 前後の2つの項のカップルをくっつけ合わせると、
という計算式になります。シンプルになった計算式を根性で計算してみると、
という解が得られます。これは前から順番通りに計算していた頃よりかなり計算過程が楽でしたよね？？ その理由としては端数が消えるように「交換法則」と「結合法則」を使ったからです。
問題2. 
この計算式も見た目がかなりごっついですね。 光の速度でこの問題をとくために、交換法則と結合法則をつかってやりましょう。
まず、交換法則を使って計算の順番を入れ替えます。なぜなら、8134というモンスターを倒す前に
交換法則をつかうと、
という計算式に変化します。結合法則を利用して計算を進ませてやれば、
という答えを抽出できます。ね？カンタンになりましたよね！？
交換法則と結合法則は以外にも便利だった。
ここまで紹介してきた「交換法則」と「結合法則」はいかがだったでしょうか？！？数学の教科書ではちらりと一瞬しか2つの法則を紹介していません。ただ、例題で分かる通り、
交換法則と結合法則を使えば計算問題がカンタンになります。
まるでその様子はドラえもんのスモールライトのごとく。交換法則と結合法則という2つの道具を難しい計算式にあててやれば、小さくなってしまいます。しかも交換法則と結合法則はドラえもんがいなくても使えちゃいます。 22世紀まで待たなくて済みそうですね。
それでは、また今度です。
Ken
