【中学数学】絶対値の問題を2秒でクリアするコツ
中学数学で登場する絶対値の問題を2秒でしとめる??
絶対値の意味を理解したけど、問題がイマイチ苦手だ・・・・
絶対値の問題を2秒か3秒ぐらいで解いて女子にモテたい・・・
そんな悩みを抱えていませんか??
絶対値の問題は必ず中学1年生の最初の中間テストで出題されます。絶対値の数学問題をスラスラとけないと他の問題に時間をさけなくなります。ひとによっては、絶対値の問題で頭をひねりすぎて試験時間いっぱいになってしまうかもしれません。
そんな苦しい状況にはまらないためには、絶対値問題の出題パターンをおさえることが大切です。中間テストでいい点数をとって悠々自適に暮らしましょう!

はい。
今日はそんな流れで、中間テストで使える「絶対値の問題を2秒でとくコツ」について記事をかいてみました。テスト勉強で絶対値の問題に苦手意識を持っている方は参考にしてみてくださいね。
中学数学で登場する絶対値の問題は2種類しかない
中学数学テストで現れる絶対値の問題は2種類しかありません。
ポケモンの数である719種類と比較すると小さい数であることがわかります。
テスト問題をつくる数学の先生ごとに問題の詳細は異なります。厳しい先生は生徒を泣かすような数学問題を練り上げ、いつもニコニコしている優しい先生は思わず。顔になってしまう問題を出題しますよね。??
ただ、絶対値の問題の本質を追い求めると、次の2種類の問題が浮かびあがってきます。
- 整数の絶対値をこたえる問題
- 絶対値を整数に変換する問題
つまり、図で表現するとこうなります。
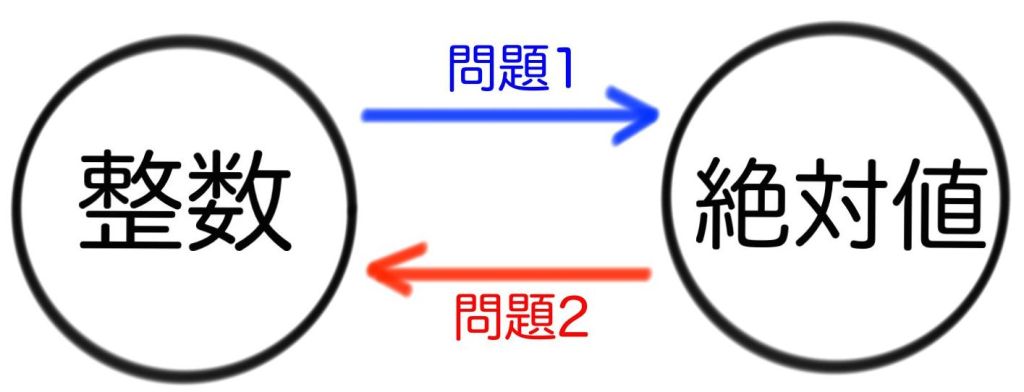
中学数学で出題される絶対値の問題は以上の2つしかないのです。種類が少ないと考えれば、テスト対策も簡単にできますよね。
絶対値の問題をクリアするために、絶対値の問題タイプについて詳しく見ていきましょう!
整数を絶対値に変換する問題
まずは整数を絶対値になおす問題です。たとえば、-90や-37や+2の絶対値を答えろこらお!といった問題です。ここでの問題解法のコツは、
整数の符号を100%無視する!
ということです。超シンプルですね。
数字の前についてる符号(+か−)をなかったことにすればいいのです。現実世界で人の存在を無視することはイジメになります。だが、しかし、絶対値の問題ではとことん符号くんを無視しましょう。
「整数を絶対値に変換する問題」の具体例として、以下の2つの問題があげられます。
(1)次の数の絶対値を答えなさい!
ひとつめの典型的な絶対値の問題は、「○○の絶対値を教えて?ねえ?」という問題。これはむちゃくちゃシンプルな問題です。筆をにぎる瞬発力があればものの2秒で解法できます。
たとえば次のような絶対値の問題があったとしましょう。
次の数の絶対値をいいなさい。
(a) -9
(b) +16
(c)-0.0008
(d) 3/8
ここでぼくらがすべきことは「数字の符号」を無視すること。これだけです。たとえば、(a)の-9でしたら、
数字の前のマイナスの符号を無視して、答えは「9」ということになります。
もし(d)の問題のように「+も−も数字についていないパターン」の場合はどうすればいいのでしょうか??
こういう場合は、問題の数字をそのまま答えてやりましょう!符号がついていない整数は「正の数」ですので、絶対値と実際の整数の値は一致しています。
ちなみに各問題の答えは、
(a) 9
(b) 16
(c)0.0008
(d) 3/8
です。数字の符号を無視するだけ?? とてもシンプルでしょう!?
(2)次の数字を絶対値の小さい順に並べ替えろ!
お次は、無造作に並べられた数字を「絶対値の大小」によって並べかえる問題です。さきほどの問題より複雑そうにみえます。がしかし、やることは(1)の場合と一緒です。冷静に符号を無視しましょう!
例題としてたとえば、
次の数を、小さい方から順に並べなさい。
また、絶対値の小さい方から順に並べなさい。
-0.0008, 0.3, 98, 0, 24, -80
なんて問題があったとしましょう。まずぼくらがやることは「マイナスの符号を無視すること」です。すると先ほどの問題の数たちは次のようになります。
0.0008, 0.3, 98, 0, 24, 80
です。その次は、これらの数字を小さい順に並べ替えてやるだけ、です。すると答えは次のようになります。(左から小さい数字)
0, 0.0008, 0.3、24, 80, 98
となります。やっていることは結構シンプルですね!
これら2つの絶対値の問題のタイプをおさえておけば大抵の絶対値問題をゼッタイにクリアできます。よかったよかった。
絶対値を整数に変換する問題
2つ目の問題のタイプは「絶対値から整数になおす」問題です。ある絶対値をもちうる整数を答えろごらあ!という問題です。ここでの問題解法のポイントはただ一つ。それは、
ある絶対値をもつ整数は正・負の2つ存在している(0をのぞく)
ということです。

理解を深めるために以下の例題を覗いてみましょう。
絶対値が7以下の整数をすべていいなさい。
この問題でまずはじめにぼくらがすることは、「絶対値が7である整数」を考えることです。「ある絶対値をもつ整数は正・負の2つ存在している」ということに気をつけると、
絶対値7をもつ整数 = -7と7
ということがわかります。これがわかればこの絶対値の問題がとけたも同然。問題が求めていることは「絶対値が7以下の整数」です。7の場合と同様に6以下のケースを考えてみます。すると、
絶対値6をもつ整数 = -6と6
絶対値5をもつ整数 = -5 と5
絶対値4をもつ整数 = -4と4
絶対値3をもつ整数 = -3と3
絶対値2をもつ整数 = -2と2
絶対値1をもつ整数 = -1と1
絶対値0をもつ整数 = 0
となります。ここで注意が必要なのは最後の「整数0」の場合です。整数ゼロは例外で「正負」の2つの整数が存在していません。絶対値0をもつ整数は0しかないという点に気をつけましょう。
すると、この問題の答えはつぎのようになります。
-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7
の合計15個ですね!
中学数学で登場する絶対値の問題はシンプル
中学数学には大きくわけると以上の2種類しかありません! たった2種類ですよ?? 割り箸を1つ使えば数えられちゃいます。わ、割り箸ですよ?? ものすごくシンプルですね。
中間・期末テストで「絶対値の問題」が出題されそうになったら、この数学の記事を読み返してみてください。きっと、いま取り組もうしている問題が上の2種類のどちらかであるはずです。
それでは、また今度です!
Ken