文字式の分数計算問題は4つのパターンしかない！？
こんにちは、2日連続でスパゲッティーを食べたKennyだよ。
文字式の分数の問題に苦手意識持ってないかな！？ そうそう、文字式の分数問題。
たとえば、
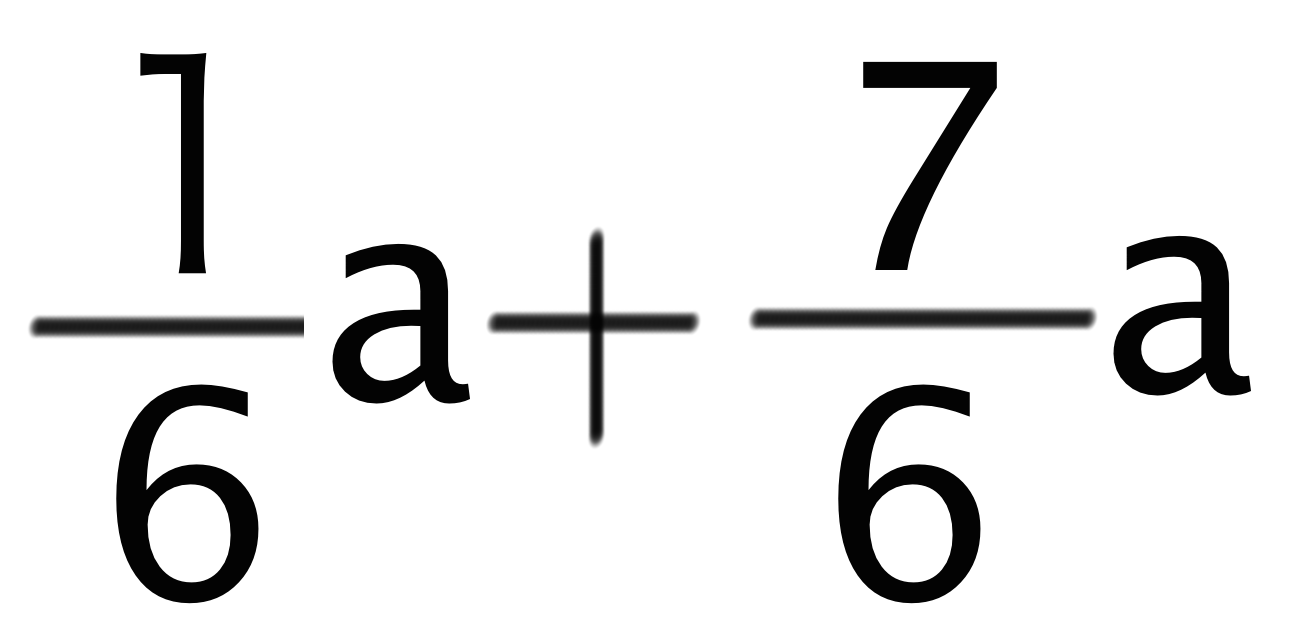
とか、
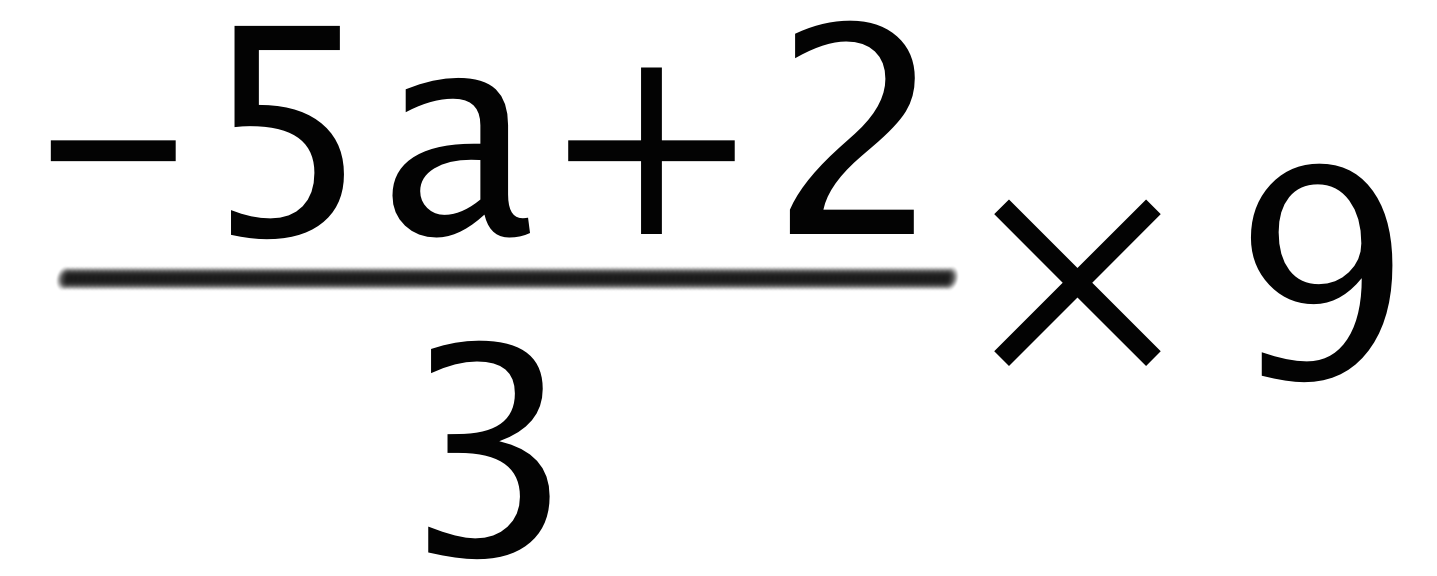
とか。こんな感じの分数の文字式の計算ってじつは4つのパターンしかないんだ。
えっ。文字式の分数問題が苦手だって？！？
今日は苦手を克服するためにもKennyが「文字式の分数問題」のパターンを4つ紹介するね。そんでもって、とっておきの解き方も紹介しちゃうよ。中間テストが近づいた時に参考にしてもらいたいね。
文字式の分数問題の4つのパターン
それじゃさっそく4つの文字式の分数問題のパターンを紹介してみるね。
パターン1. 分数＋分数（分母がいっしょ）
1つ目のパターンは分数と分数の計算。
これは文字式の分数の計算の中で一番カンタンなパターンだからしっかり覚えておこう。
たとえば、
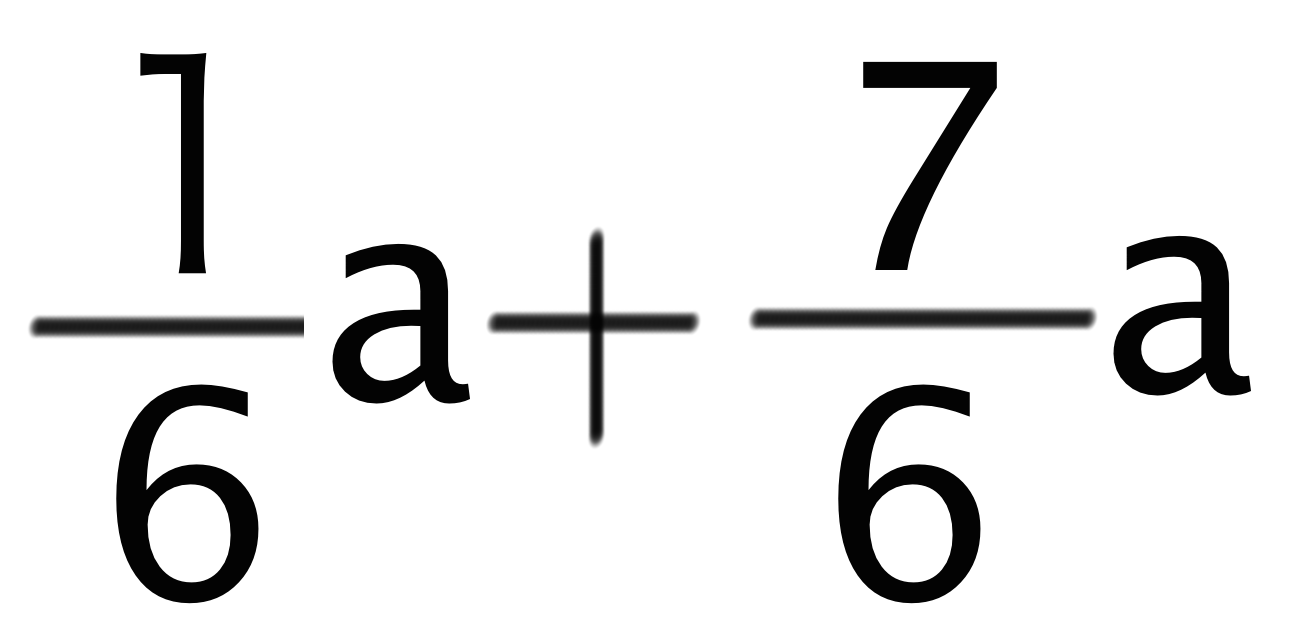
この文字式では2つの項の分母が「6」で等しいよね？？ こういうときは、
分子をそのまま足してあげちゃえばいいんだ。
2つの項の分子はそれぞれ「1」と「7」だから「1+7=8」だよね？？ よって、この分数の文字式の計算問題は、
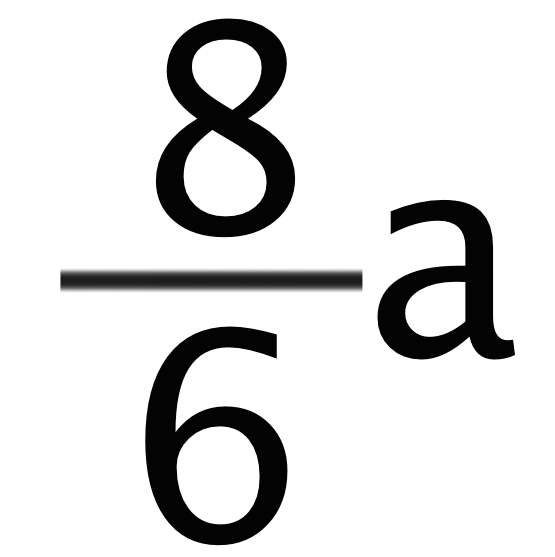
という答えになるね。ただし、
分数の文字式の計算では必ず「約分できるかどか」を確認するようにしよう。この文字式の答えでいえば分母の「6」と分子の「8」はお互い「2」で割れるよね？？ っていうことは約分できるってこと。よってこの分数の文字式の計算の答えは、
になるよ。約分をくれぐれも忘れずにね！！
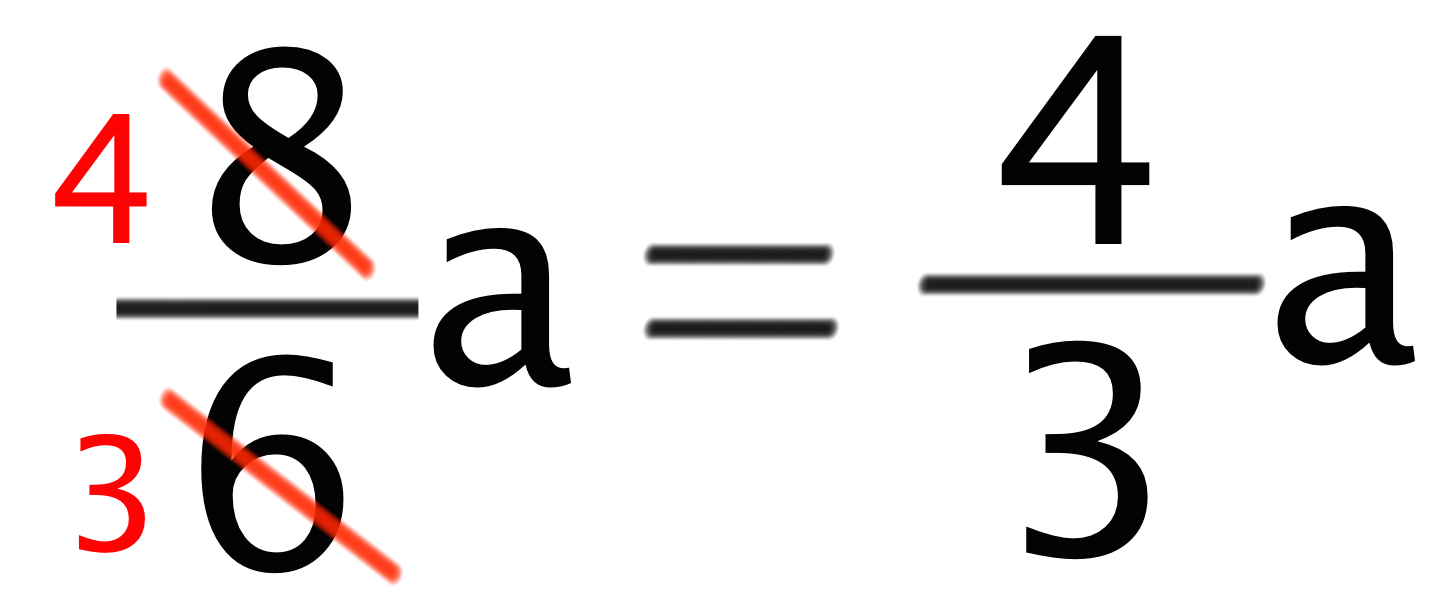
パターン2. 分数＋分数（分母がちがう）
2つ目のパターンは、分母がちがう分数を足し合わせる文字式だ。
このパターンでは、
分母を通分する
というステップが入るからちょっとややこしいね。例題をみてみよう。
たとえば、
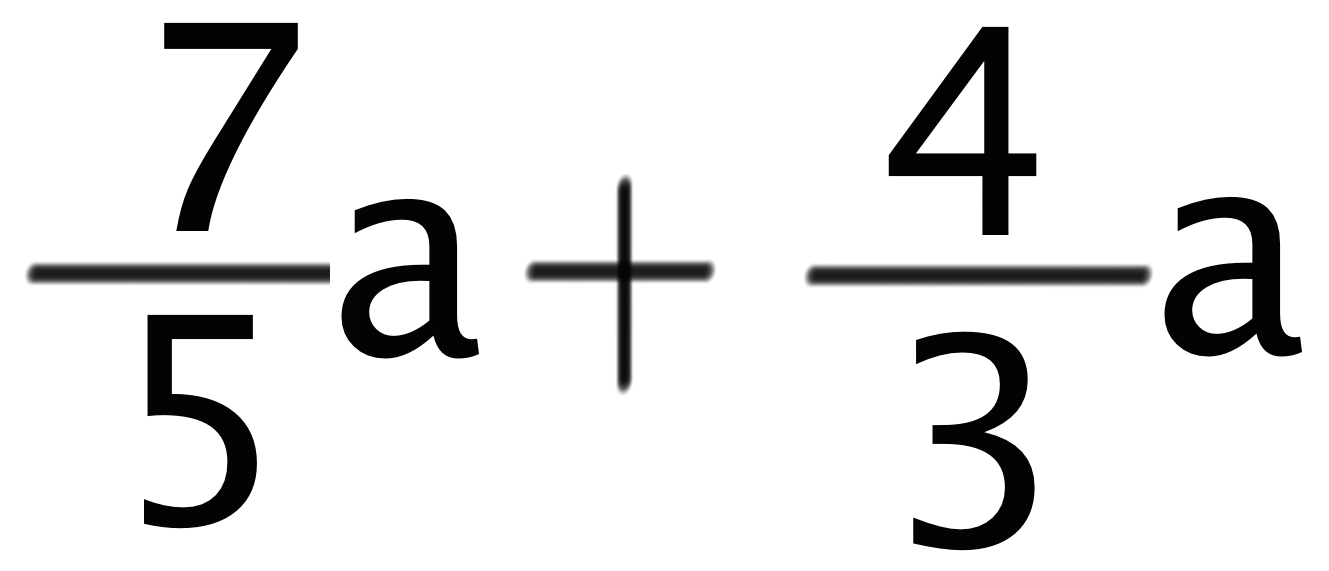
分母が違う文字式の分数足し算では、まず通分しなきゃいけないんだ。通分って小学校で習ったよね？？
分母の「5」と「3」の最小公倍数を探して、そいつを新しい分母にしちゃえばいいんだよ。
この場合、「5」と「3」の最小公倍数は「15」だから、2つの項の分母を15にそろえちゃおう。すると、
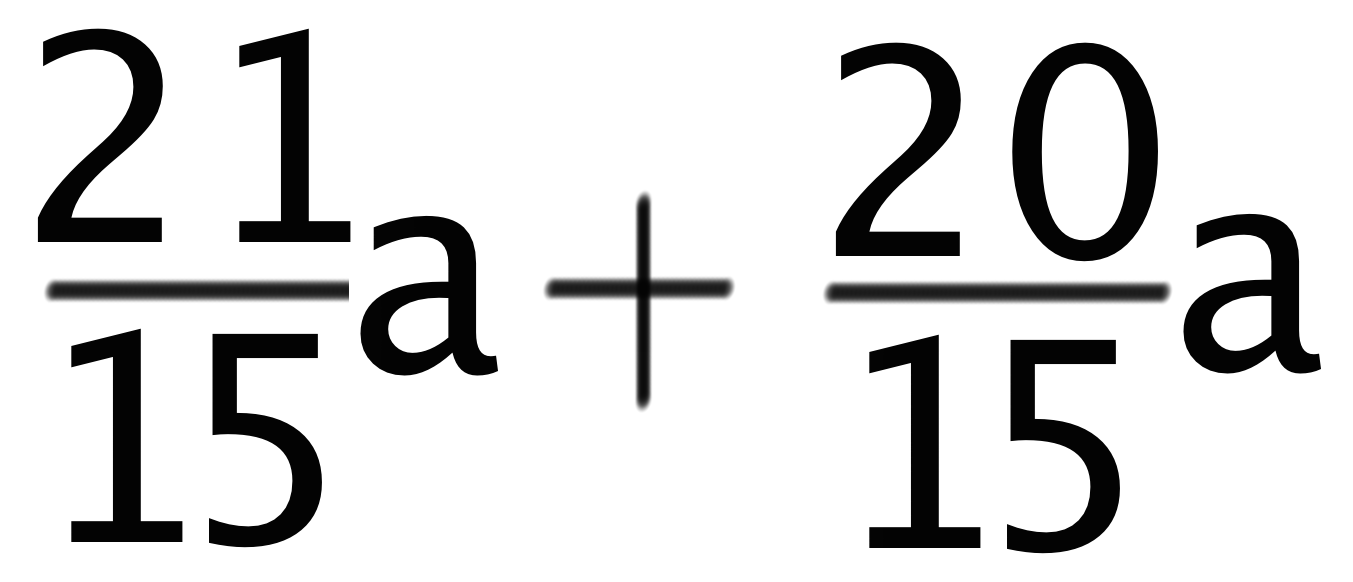
こうなるね。分母が等しくなったから、2つの文字式の分数を足しちゃおう。
すると、
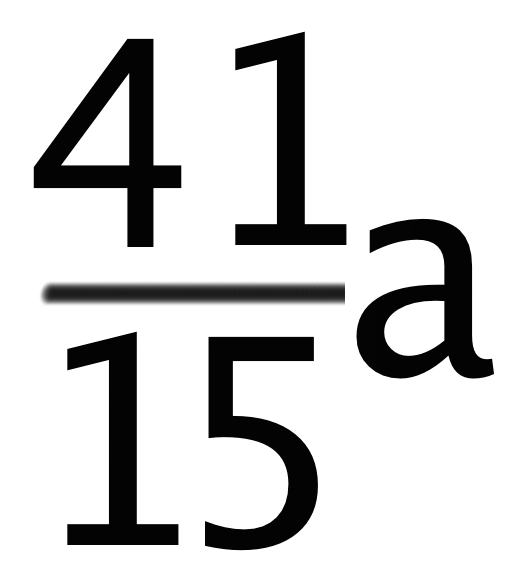
パターン3. 分数＋分数以外（整数・文字）
3つ目のパターンは分数と分数以外の文字の足し算だよ。たとえば、
という文字式を例にとって説明しよう。
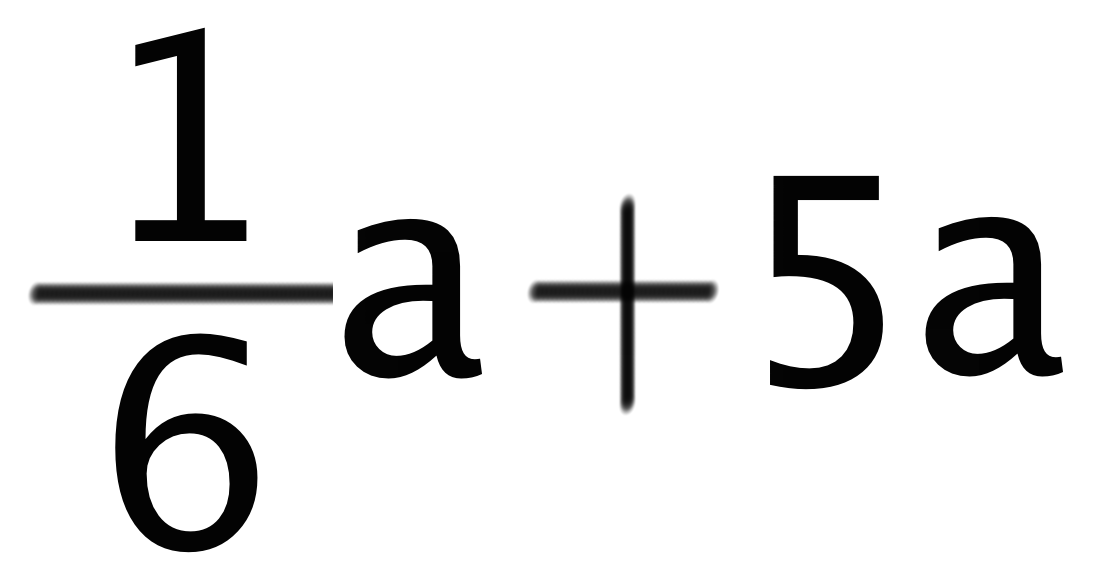
こういうときは、分数＋分数の形に直してから計算するようにしよう。さっきの
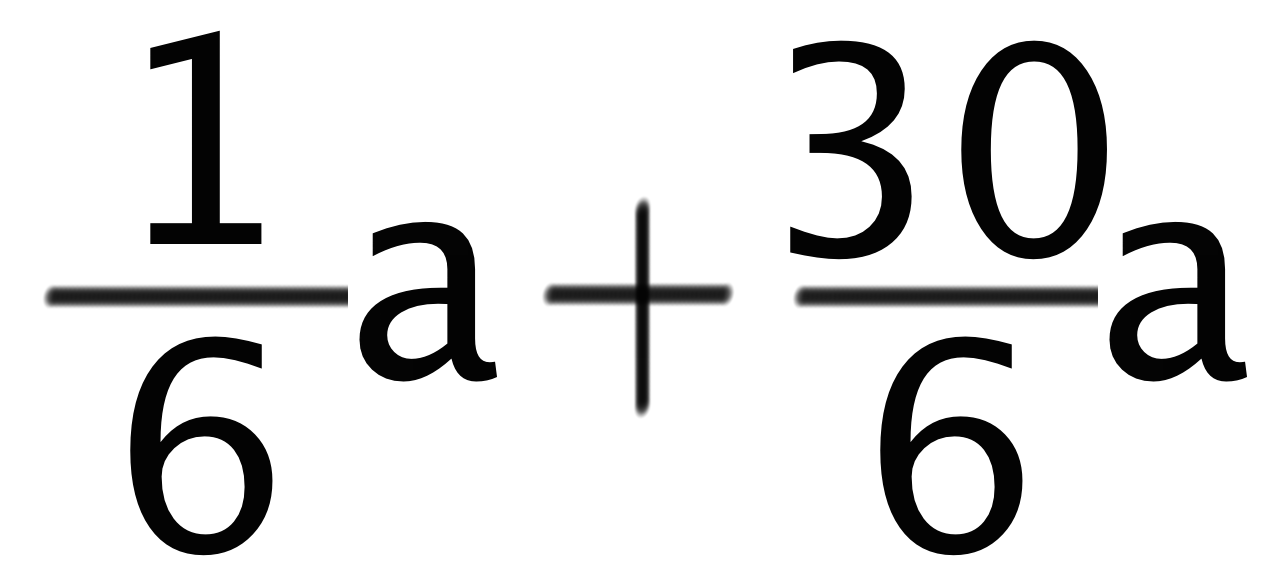
ってなるよね？？ あとは分子を足してあげるだけ。よって、答えは
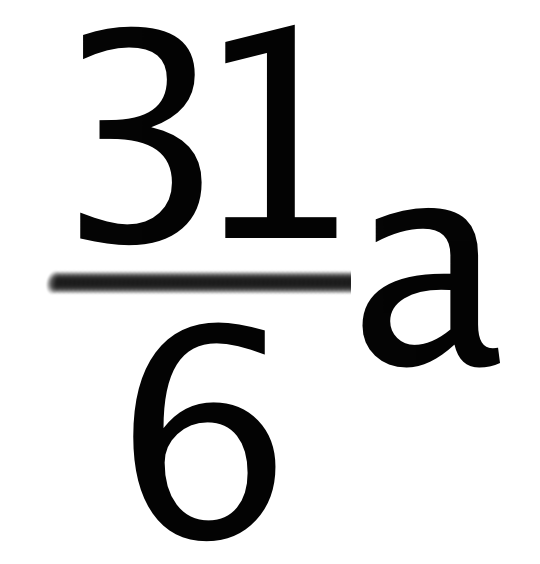
パターン4. 「分数」×「整数」
最後のパターンは分数の文字式に「整数」を掛けたり割ったりした問題。たとえば、
という分数の文字式をみてみよう。
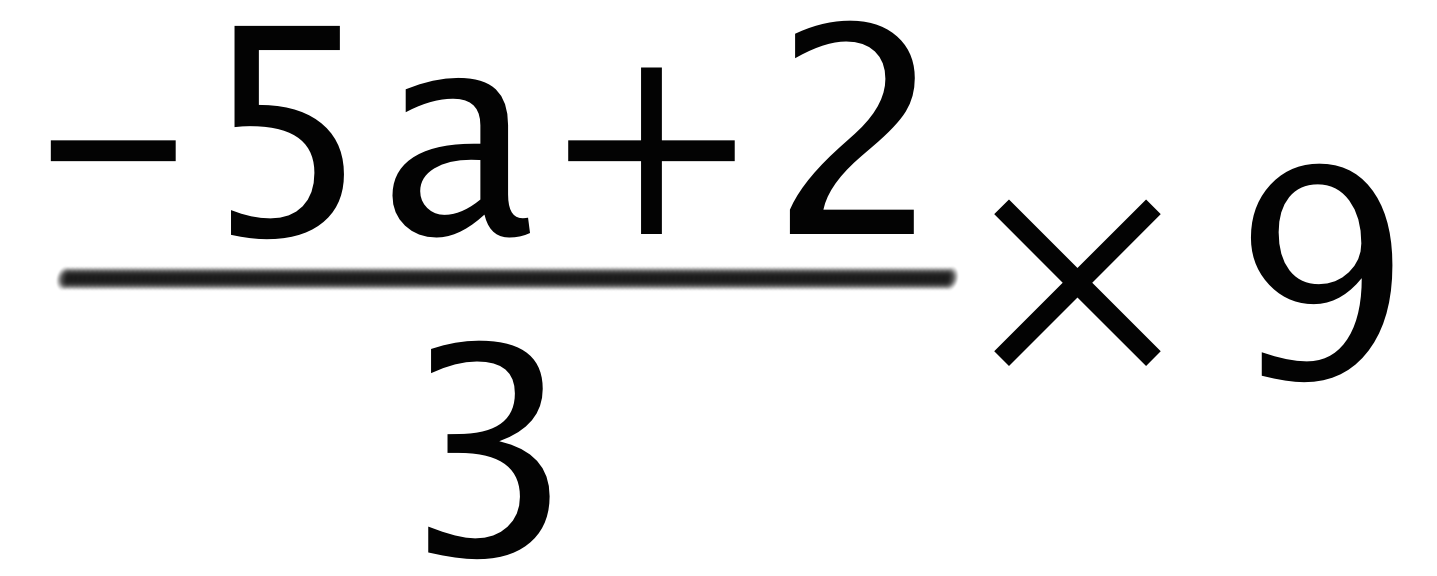
このタイプの文字式問題は次の2つのステップで攻略しちゃおう。
- 分数を分子と分母にわける
- 分母と整数の計算をする
さっきの例題でいえば、まずはこんな感じで分数を分母と分子に分解しちゃうんだ。
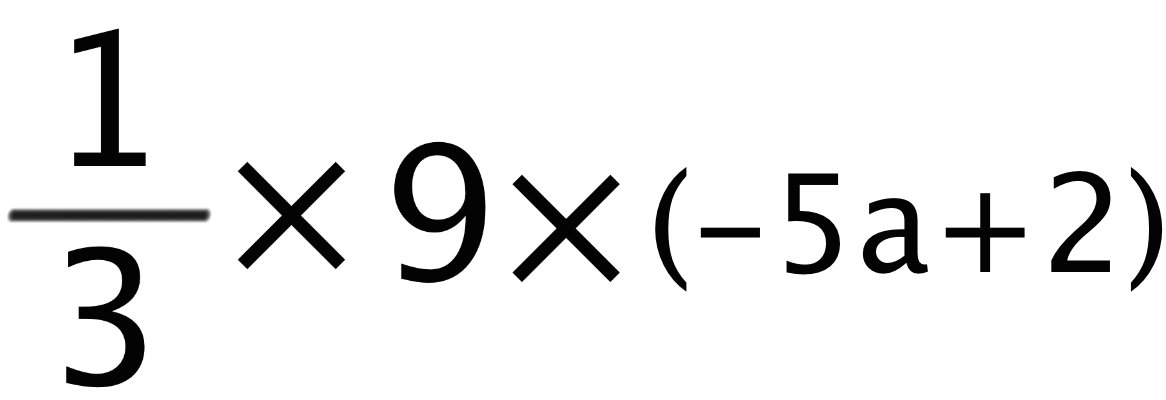
そっから、分母だけの分数と整数を掛けてみると、
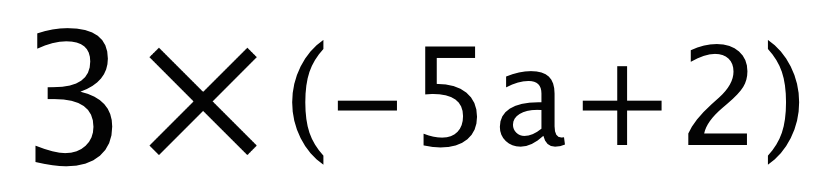
ってなるんだ。これを分配法則をつかって解いてあげると、
このタイプの計算で注意することは、
分配法則を間違えずに計算し終えることだ。カッコ内の1つの項にしか掛けなていないミスがあるからね。十分に気をつけよう！
分数の文字式の計算問題も楽勝だね！
ここまで分数の文字式の計算問題を解いてきたね。どうだったかな？？
学校のテストの分数の文字式の問題はゼッタイに4つのパターンに当てはまるよ。だから、テスト前にこの記事を読んじゃえばゼッタイに大丈夫。復習を忘れずに。
それじゃねー
Kenny
