中学1年数学で勉強する「項」の意味は？？
中学数学の単元「正の数・負の数」では、「項 (こう)」という言葉が登場します。
「項」なんて小学校で勉強しなかった数学用語ですよね？
数学が苦手な中学生の方はきっと、ぜんぜん、ピンときてないはず。
そこで今日は、中学数学で登場する「項」の意味を復習していきます。
中学数学の「項」の意味とはいったい？？
さっそく、中学数学で勉強する「項の意味」を復習してみましょう。
中学1年生の数学の教科書には「項」の意味がつぎのように紹介されています。
加法だけの式、
$$(+7)+(-8)+(-5)+(+9)$$
で、
$$+7, -8, -5, +9$$
を、この式の項（こう）といいます。
つまり、
ある式を「足し算だけ」の式に直したとき、＋記号に挟まれてる奴らが項なのです。
たとえば、
$$2-8+7$$
という式があったとしましょう。
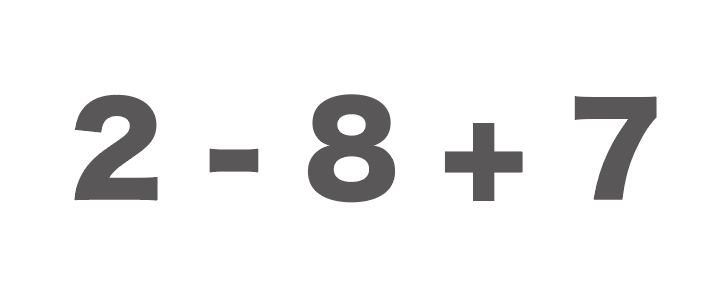
このとき、この式を加法（足し算）だけの式に直してみると、
$$2+(-8)+7$$
になりますね。
そのため、この式の項は、＋記号にはさまれている３つの塊である、
- 2
- -8
- 7
になるわけです。
掛け算・割り算が混じっていたら項はどうなる？？
だいたい項の意味もわかってきましたが、あと注意することが一点。
それは、掛け算・割り算が混じっている場合の項の見つけ方です。
掛け算・割り算が混じっている式の場合は、
掛け算や割り算を一度計算してしまってから、項を探すようにしましょう。
たとえば、
$$2 × 3 -3 ÷ 6 × 2 – 7$$
という式があったとしましょう。
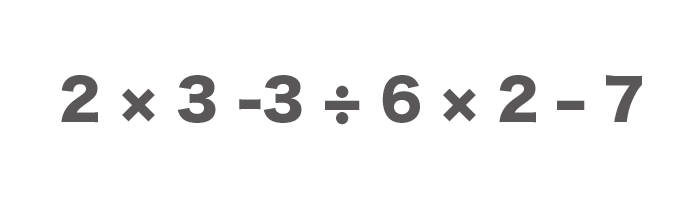
こんな感じで、掛け算と割り算が入り乱れている式の場合は、
まずは掛け算割り算を計算します。
すると、
$$2 × 3 -3 ÷ 6 × 2 – 7$$
$$= 6 -1 -7$$
となりますね。
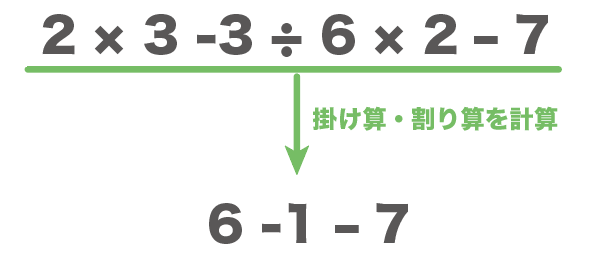
ここまでくれば、先ほど同様に、式を足し算だけの式に直してあげればいいので、
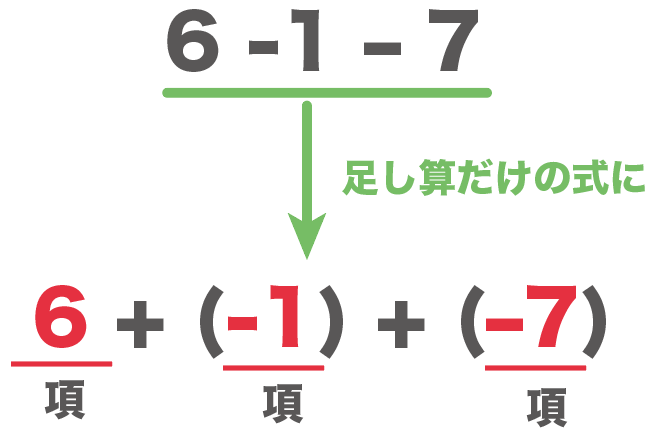
$$6 -1 -7$$
$$= 6 +(-1)+( -7)$$
となります。
結論、この式における項は、＋に挟まれている、
- 6
- -1
- -7
の3つということになります。
項は「足し算だけの式に直した時に、＋に挟まれてる塊たち」のこと
以上が、項の意味でした。
最後に復習しておきましょう。
項とは、
足し算だけの式に直した時に、＋記号に挟まれている塊のこと
でしたね。
だから、とある式で項を探したいときは、まずはその式を足し算だけの式に書き換えてみればいいのです。
項はこれから３年間活躍する重要な数学用語なのでしっかりここら辺でマスターしておきましょう。
それでは！
Ken
