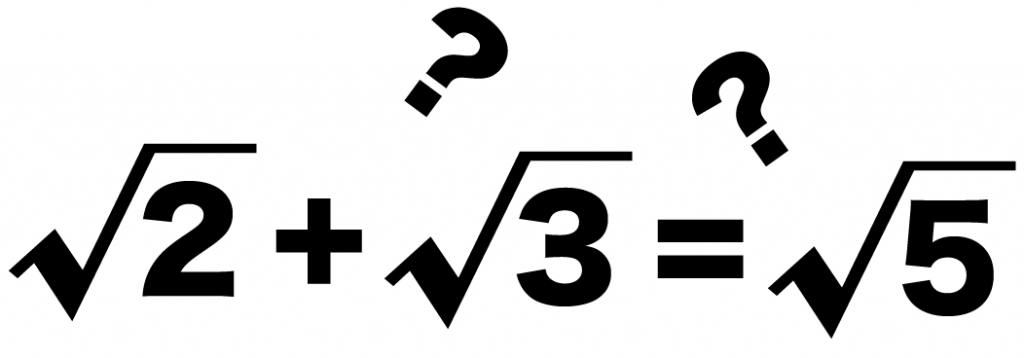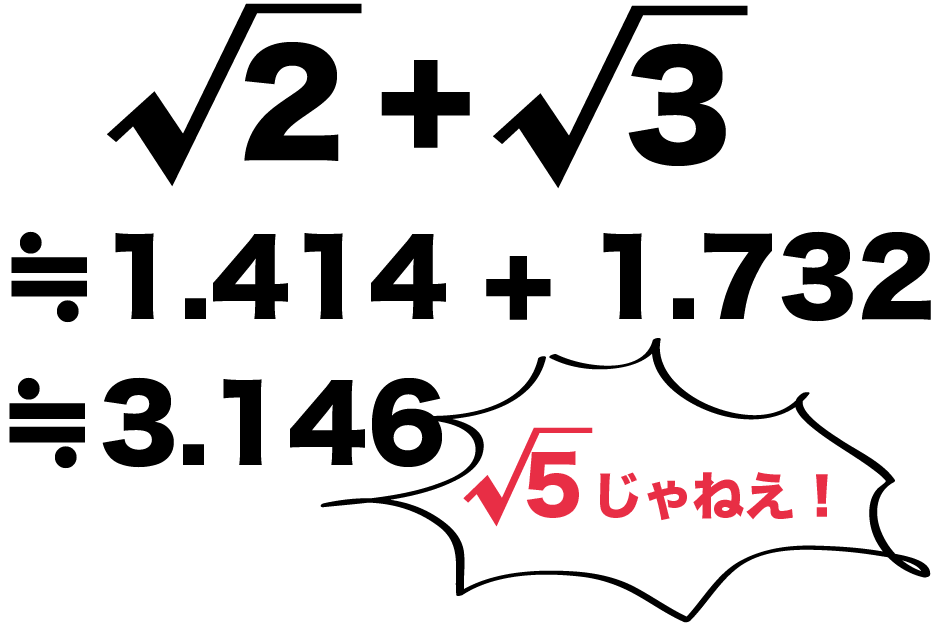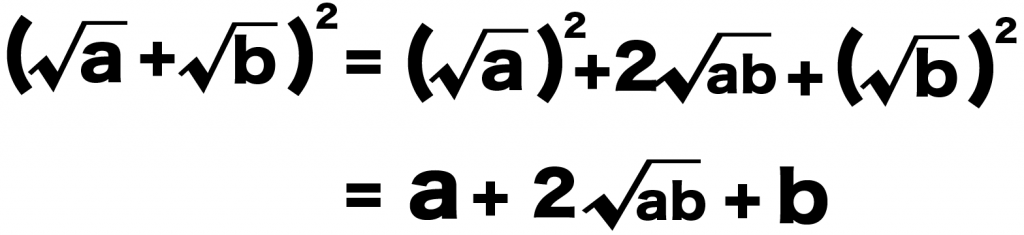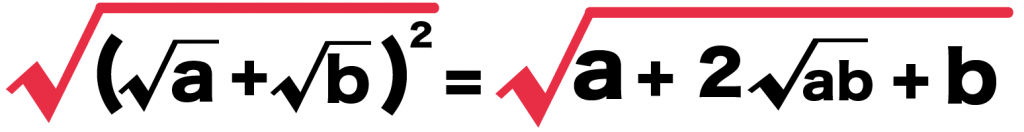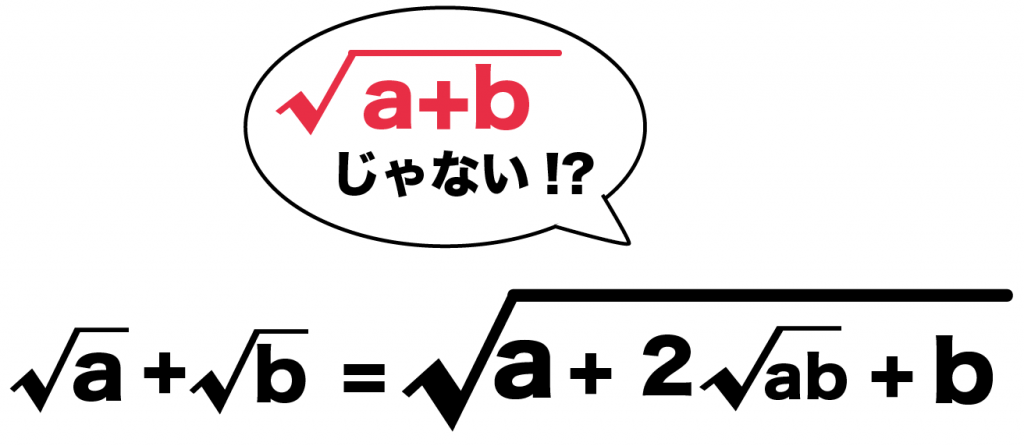ルートの中身は足し算・引き算しちゃダメ？？
こんにちは！この記事をかいてるKenだよ。時差に要注意だね。
ルートの計算で間違いやすいのは、
足し算・引き算
だ。
よくあるミスで、
ルートの中身を足し算・引き算しちゃう
ってやつがある。
たとえば、
√2 + √3
だったら、中身の2と3をたして、
√2 + √3
=√5
みたいな感じでね。
だけどね、この平方根の足し算の仕方は、
とんでもなく間違っているんだ。
ほんとうに。
とんでもなくね。
ルート（平方根）の中身を足し算・引き算しちゃダメ！！
なにがっあってもダメ。
地球が反転しても、磁力がおかしくなっても、ダメ。
√の中身はゼッタイに足し算・引き算しちゃいけないんだ。
まじで、ムリ。
平方根の近似値で計算してみればきづくはずだ。
√2と√3の近似値はそれぞれ、
だったよね？？
計算すると、
√2 + √3
≒ 1.414 + 1.732
≒ 3.146
になるね！
3.146っていう数字はあきらかに√5の近似値じゃない。
だって、√5の近似値は、
2.2360679（富士山麓オームなく）
だったもんね？？
足し算・引き算では中身がおなじ平方根の整数だけ計算しよう。
たとえば、
√a +√a
= 2√a
みたいな感じでね。
計算の仕方は文字式の足し算・引き算に似てる。
文字式の計算でも、おなじ文字しか足し引きしちゃいけないよね？？
それと同じさ。
なぜ、ルートの中身を足し算・引き算しちゃいけないの？？
でもさ、
なんでルートの中身を足し算・引き算しちゃいけないのかな？？
雰囲気的にはいけそうな気がするもん。
今日はせっかくだから、
なぜ平方根の中身を足し算、引き算しちゃいけないのか
をみていこう。
Step1. 「√a + √b」を2乗してみる
まずは、
√a + √b
を2乗してみよう。とりあえずね。
展開の公式で計算すると、
( √a + √b )^2
= (√a)^2 + 2√ab + (√b)^2
= a + 2√ab + b
になるね！
Step2. 「√をつける」
さっき生み出した等式の、
( √a + √b )^2 = a + 2√ab + b
両辺に√をつけてみよう。
なぜ、ルートをつけるのかというと、
( √a + √b )^2
から2乗をとっぱらいたいからだ。
さっそく、左と右にルートをつけてやると、
√{( √a + √b )^2} = √(a + 2√ab + b)
になるね！
左辺の中身は（√a+√b）の2乗になってるから、
√と2乗をそのまま消せる。
すると、
√a + √b = √(a + 2√ab + b)
になるね。
このことからわかるのは、
√a + √b = √(a + b)
にならないってことだ。
余計な「2√ab」が入ってるのさ。
まとめ：ルートの足し算・引き算は文字式のように計算せよ！
ルートの足し算・引き算で気をつけるべきこと。
それは、
ルートの中身をたしひきしちゃいけない
ってことだ。
文字式の足し算・引き算とおなじ計算方法
っておぼえておこう。
そんじゃねー
Ken
