3分でわかる!相似比から体積の比・表面積比を求める公式
相似比から体積の比を求める公式ってあるの??
こんにちは!ぺーたーだよ。
相似の単元の勉強はどうかな??
相似の証明問題だったり、
相似比を求める問題が出たり
あれこれ大変だね。
今日はもう1つ新しい、
相似比をつかった体積の比の求め方
を解説するよ!
ついでに表面積の比の出し方も説明するから、
セットで覚えてあげよう。
相似比をつかって体積比を求める公式
相似比から体積比をだすときは、
つぎの公式をつかってみよう。
それは、
相似比の3乗が体積比になるよ
っていう公式だ。
くわしくいうと、
2つの相似な立体があって、相似比がn:mのとき、
2つの立体の体積比は、
n^3 : m^3
になるってこと。
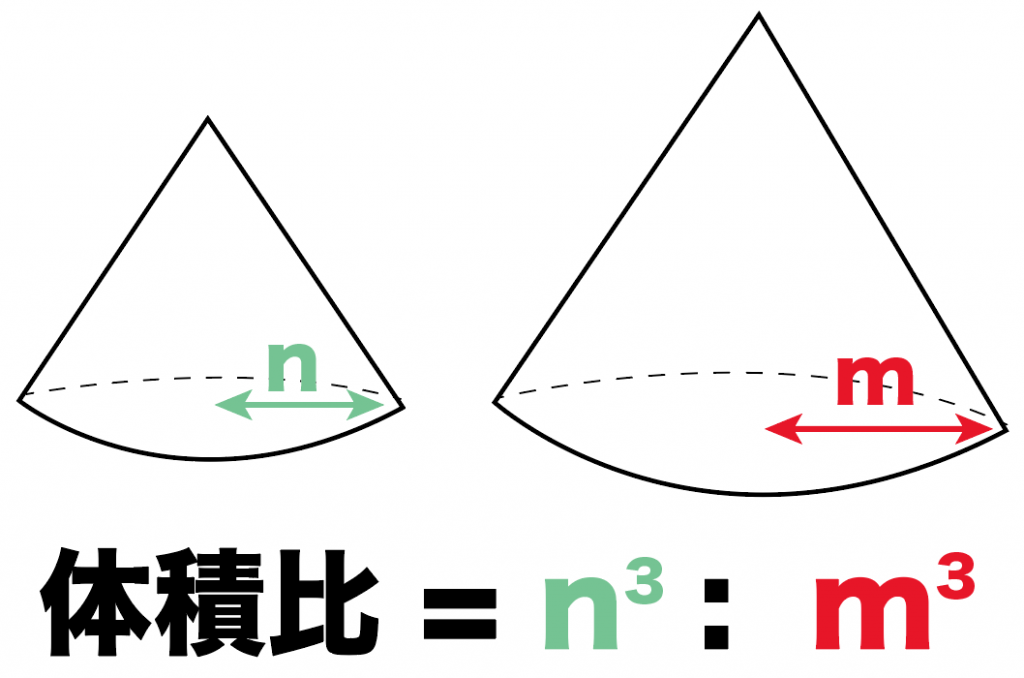
この公式で練習問題をといてみよう。
練習問題
次の円錐は相似の関係です。
体積比と表面積の比を求めてください。
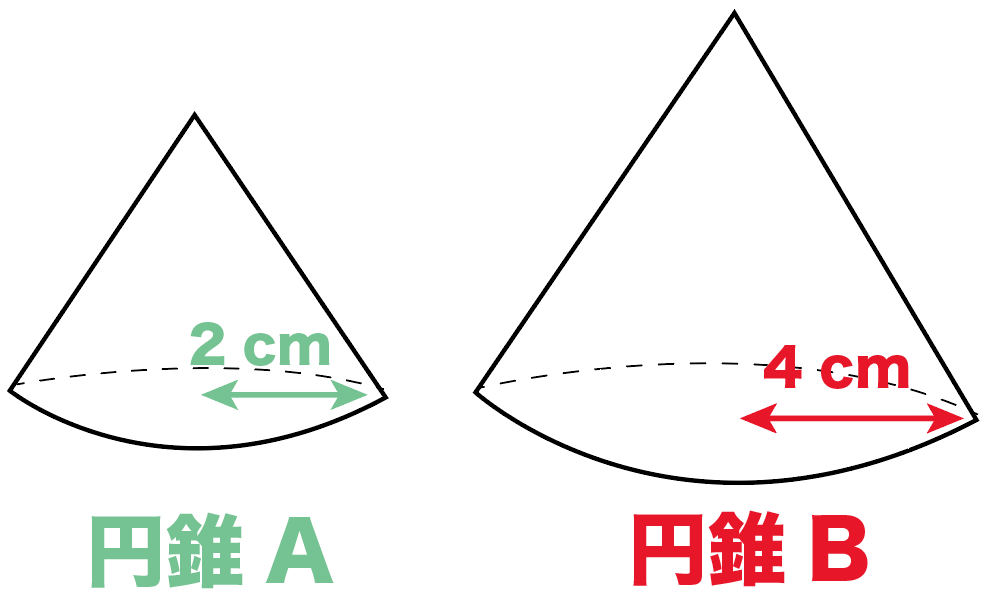
この体積比の問題は、2ステップでとけちゃうんだ。
Step1. 相似比を求めよう
立体の体積比を求めるには、
相似比
が必要なんだ。
練習問題をみてみると、
2つの円錐は相似である
ってかいてあるね。
わざわざ相似を証明する必要ないからうれしい!
さっそく相似比を求めてみよう。
対応する辺を「半径」として、相似比をもとめてみてね。
2つの円錐の底面の半径はそれぞれ、
- 2 cm
- 4 cm
だったよね??
ってことは、こいつらの相似比は、
2: 4
= 1: 2
になるんだ。
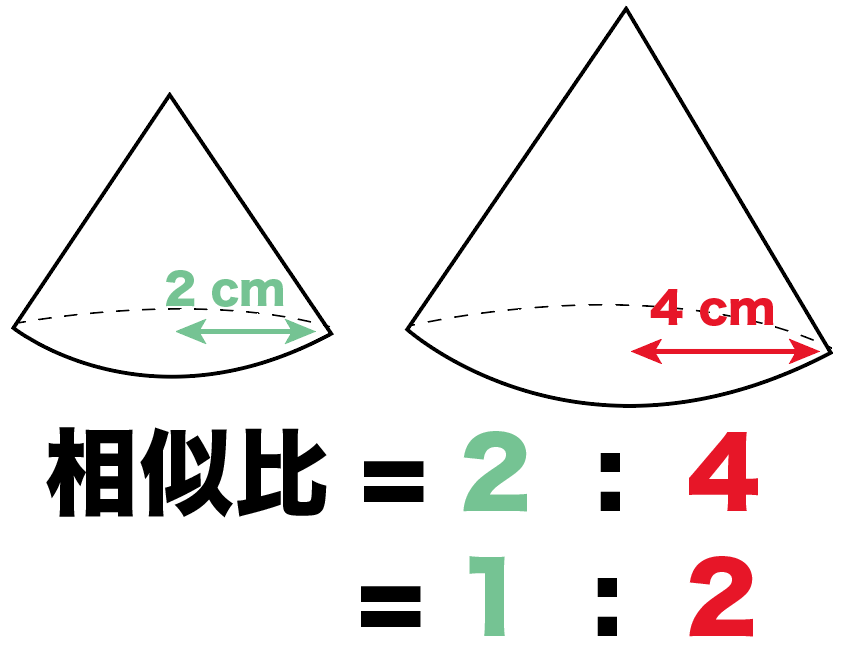
Step2. 体積比を計算
相似比が出たら、
体積比はとっても簡単!
体積比の公式の、
相似比を3乗してやると体積の比になる
を使えばいいのさ。

練習問題でも体積比の公式をつかっていこう。
相似比は1:2っていうことがわかったね。
体積比はその相似比を3乗した、
1^3:2^3
= 1 : 8
になるね。
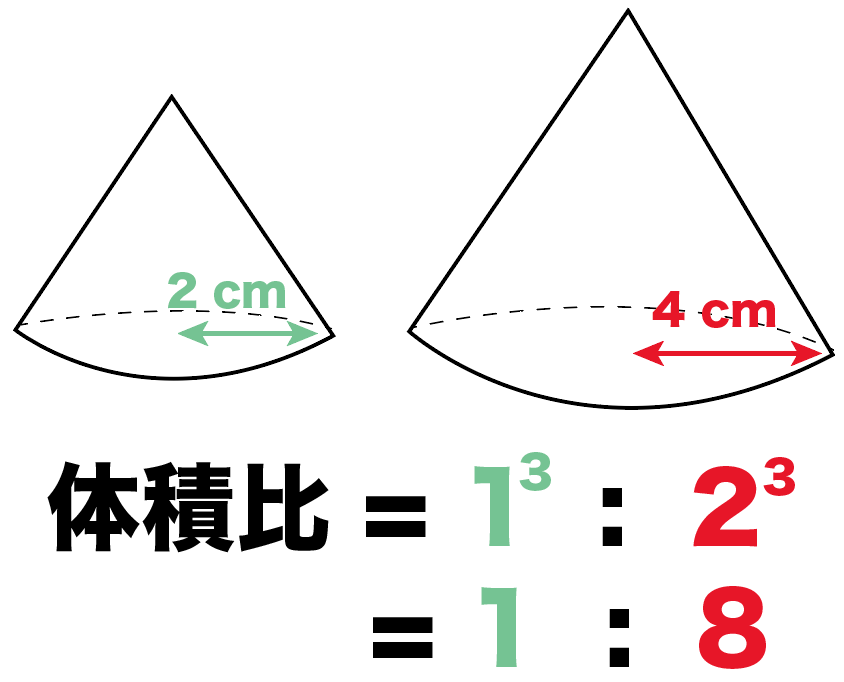
ってことで、
この2つの立体の体積比は「1 : 8」。
やったね!
体積比は何の役にたつの??
えっ。
体積比は何の役にたつのかって??
じつは、体積比がわかると、
「ある立体の体積」から「べつの立体の体積」が計算できちゃうんだ。
たとえば、さっきの練習問題で、
円錐Bの体積が80 [cm^3]だったとしよう。
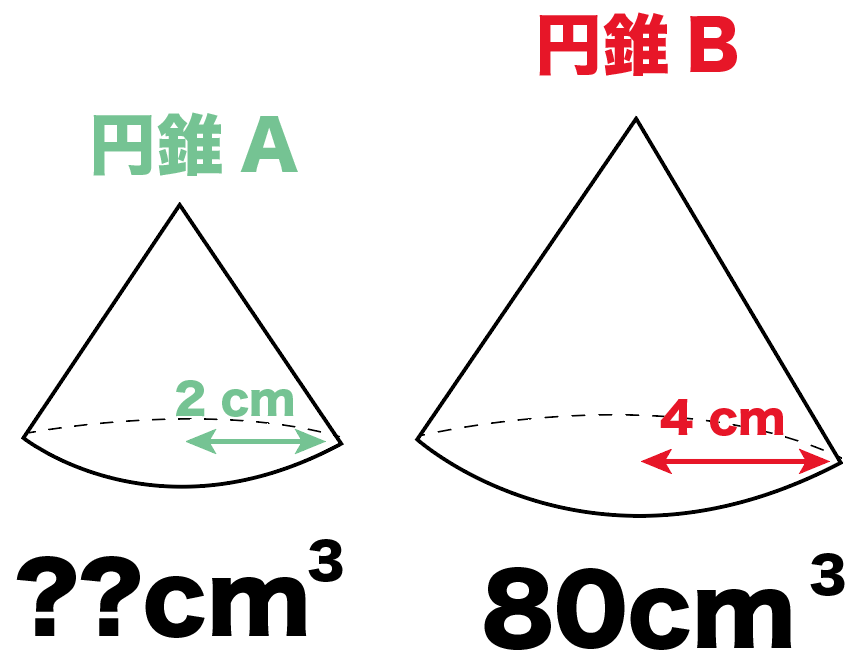
この2つの立体の体積比は、
1: 8だったよね??
ってことは、
「円錐Aの体積」は「円錐Bの体積」の8分の1。
ってことは、円錐Aの体積は、
(円錐Bの体積)×1/8
= 10 [ cm^3 ]
になるんだ。
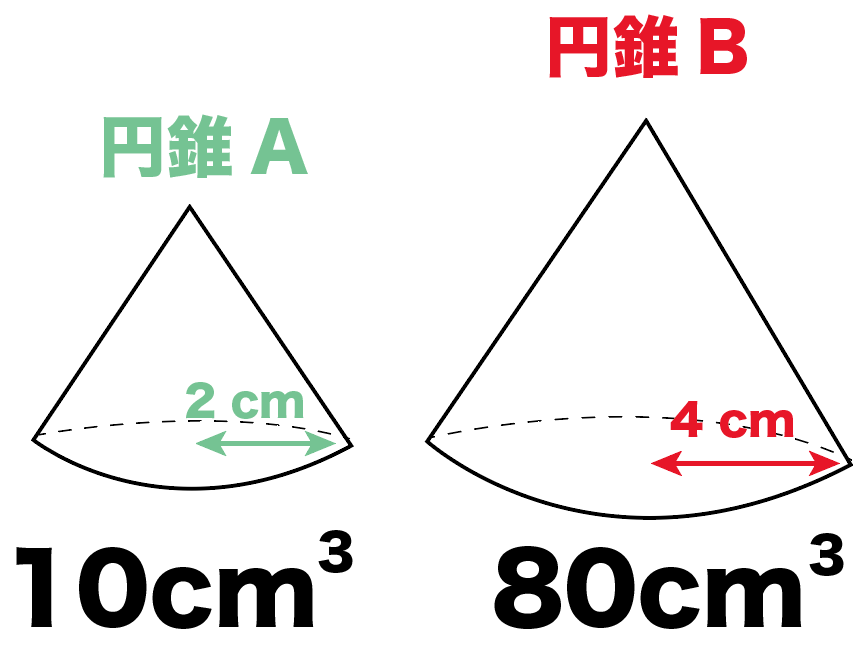
ね??
体積比をつかうと立体の体積がわかっちゃうんだ!
おまけ:相似比から表面積の比も求めてみよう!
相似比から体積比が求められたね!
おめでとう・・・・・・!!
っていうのはまだはやい。
じつは、練習問題の最後に、
表面積の比も求めなさい
ってかいてあるじゃん?
せっかくだから、表面積の比も相似比から計算してみよう。
ずばり、表面積の比の求め方は、
面積比の求め方といっしょ。
つまり、
相似比の2乗の比になってるのよ。
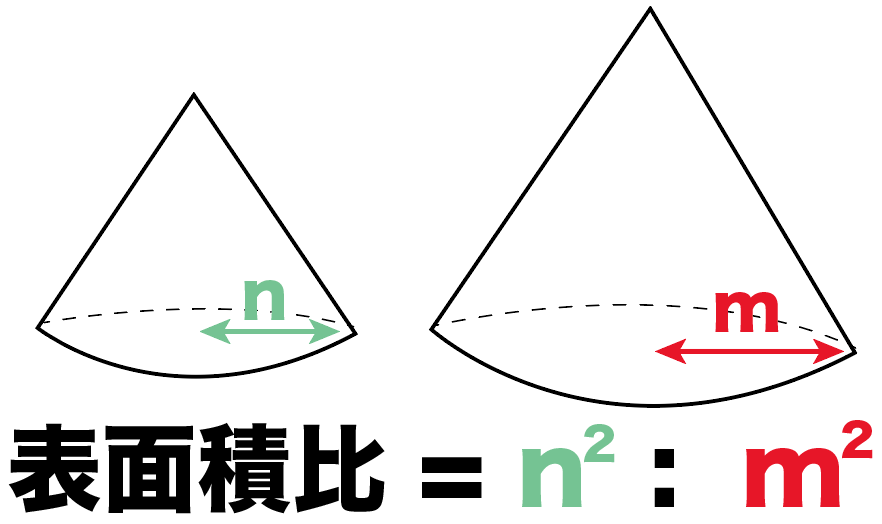
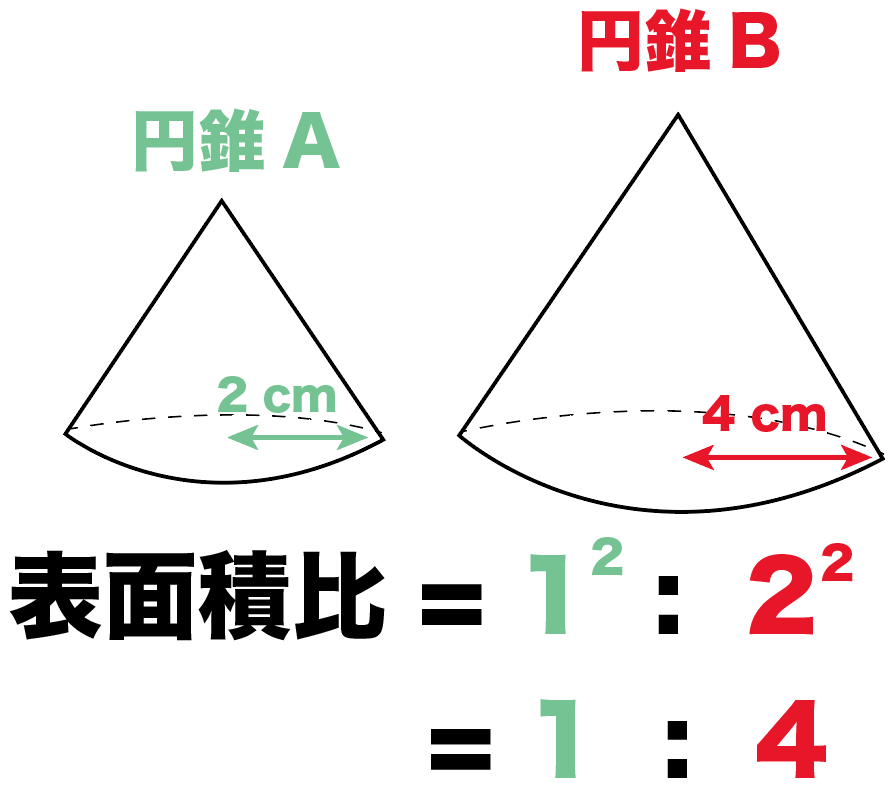
相似比が1:2の「円錐A・Bの表面積の比」は、
1^2 : 2^2
= 1 : 4
になるわけね。
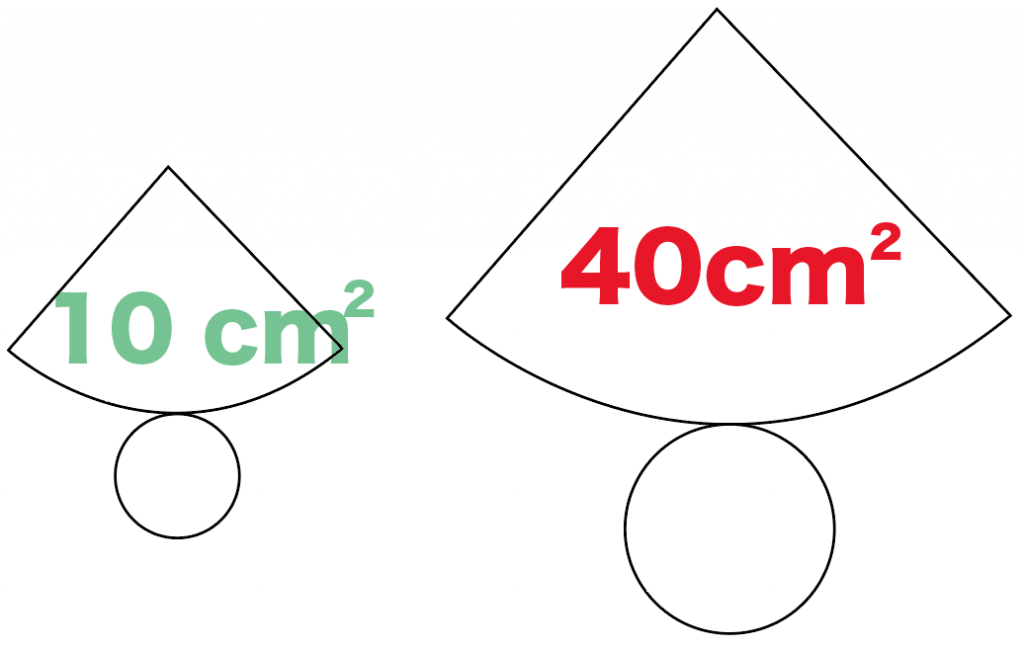
もし、円錐Bの表面積が40 [cm^2]だったら、
円錐Aの表面積は10 [cm^2]
になるわけだね。
おめでとう!
相似比から表面積の比も求められたね!
まとめ:体積の比・表面積比の公式をしっかり覚えよう!
体積の比も、表面積の比も公式を覚えちゃえば楽勝。
しっかり公式を覚えてあげようね。
問題をときまくって段々なれていこう!
じゃあ、またね
ぺーたー


