5分でわかる!三角形の3つの合同条件
三角形の合同条件ってなんなの??
こんにちは!この記事をかいているKenだよ。今日は布団をほしたね。
ある日突然、三角形が2匹出現したとしよう。
サトシならモンスターボールを用意するかもしれない。
ルフィならば仲間にしちゃうかもしれない。
でも、図形を勉強している中学生はこう思うはずだ。
どういう条件がそろえば合同になるんだろう??
ってね。

この、
「三角形が合同になる条件」のことを数学界では、
三角形の合同条件
ってよんでいるんだ。
今日はその「合同条件」をわかりやすく説明していくよ。
よかったら参考にしてみてね。
5分でわかる!三角形の3つの合同条件
三角形には、
3つの辺と、
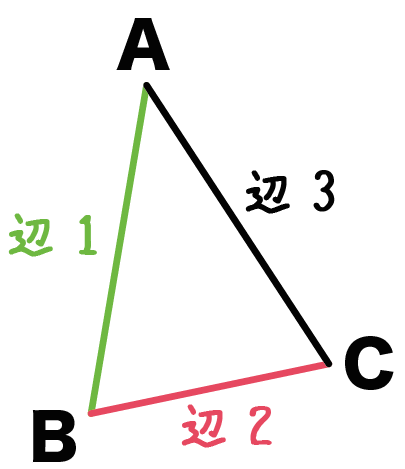
3つの角
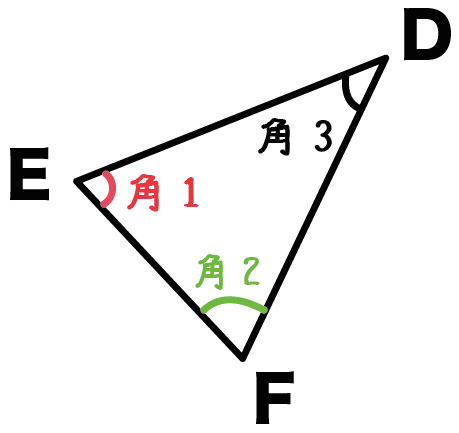
があるよね??
三角形の合同条件は、
こいつらの「どれ」が「どの位置」で等しくなっているか??
によって3つにわけられるんだ。
つまり、
「どの辺」と「どの角」が等しいかによって、
合同かどうかジャッジできるってわけさ。
順番に確認していこう!
合同条件1.「3組の辺がそれぞれ等しい」
1つ目の合同条件は、
3組の辺がそれぞれ等しい
というものさ。
つまり、
2つの三角形の辺がそれぞれぜーんぶ等しい
ってわけだね。
たとえば、下のような三角形たちだ。
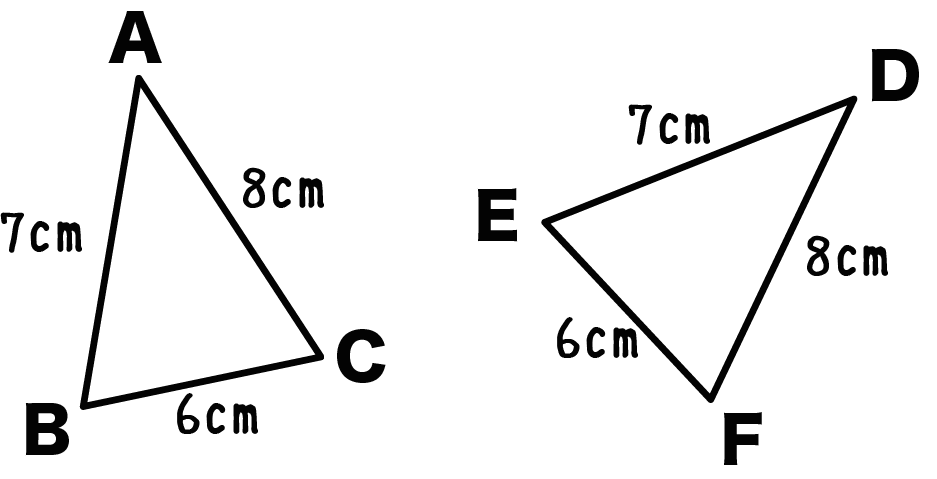
辺の長さはそれぞれ、
- AB = DE = 7 cm
- BC = EF= 6 cm
- AC = DF = 8 cm
になっている。
よーくみてみると、
3つの辺がそれぞれ等しくなっているね。
これにより、
△ABC = △DEF
がいえるのさ。
合同条件2. 「2組の辺とその間の角がそれぞれ等しい」
つぎは、
2つの辺
と、
そいつらに挟まれた角
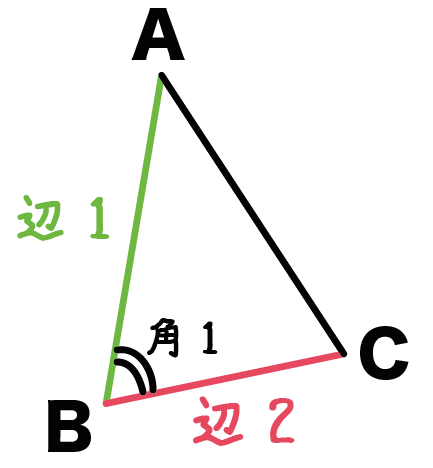
がそれぞれ等しいっていう条件だ。
たとえば、つぎの三角形ABCとDEFなんかがそれにあたる。
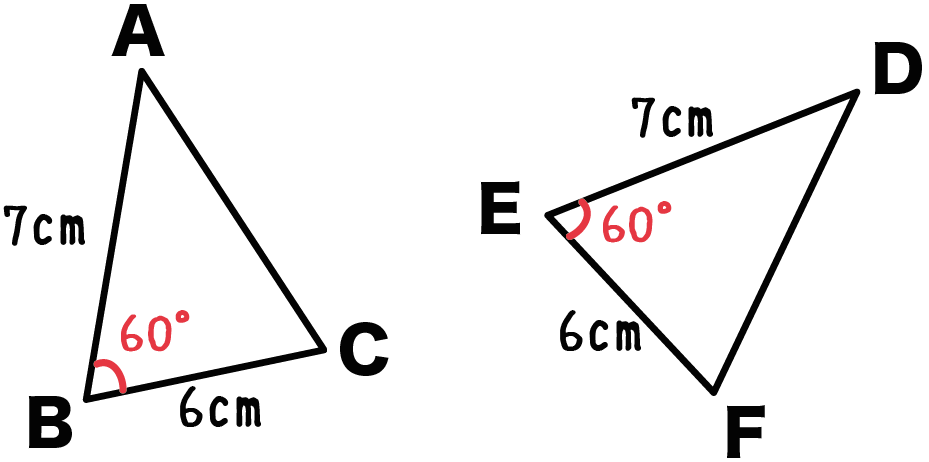
なぜなら、2組の辺が等しく、
- AB = ED = 7 cm
- BC = EF = 6 cm
その間にはさまれた角が、
- 角B = 角E = 60°
等しいからね。
こいつらは、
2組の辺とその間の角がそれぞれ等しい
っていう合同条件をみたしている。
よって、
△ABC ≡ △DEF
ってことがいえるんだ。
合同条件3. 「1組の辺とその両端の角がそれぞれ等しい」
最後は、
2つの角
と、
挟まれた1つの辺
が等しいという条件だ。
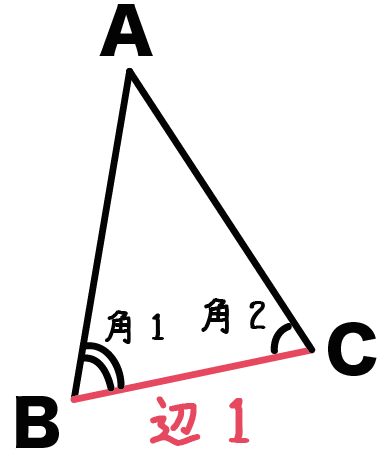
たとえば、つぎの三角形ABCとDEFみたいな感じでね ↓↓

こいつらは合同だよ。
なぜなら、
2組の角が等しく、
- 角B = 角E = 60°
- 角C = 角F = 70°
そいつらに挟まれた1組の辺が、
- BC = EF = 6 cm
等しくなってるからね。
こいつらは、
「1組の辺とその両端の角がそれぞれ等しい」
っていう合同条件をみたしている。
よって、
△ABC ≡ △DEF
ってことがいえるんだ。
まとめ:三角形の合同条件は挟みまくれ!
三角形の合同条件は、
- 3組の辺がそれぞれ等しい
- 2組の辺とその間の角がそれぞれ等しい
- 1組の辺とその両端の角がそれぞれ等しい
の3つしかないよ。
合同の証明問題で必須になってくるから、
テスト前におぼえてみてね。
そんじゃねー
Ken


