こんにちは！この記事をかいているKenだよ。おしぼりは無敵だね。
文字式の利用で、
連続する3つの整数の和の問題
ってでてくるよね。
たとえば、つぎの問題 ↓↓
例題
連続する3つの整数の和が3の倍数になる訳を説明しなさい。ただし、整数は正の数とする。
日常生活では3つの整数の和なんて考えないよね？？
だって、必要ないもん。
でもね、中2数学の問題ではよくでてくる証明なんだ。
今日はこの問題を攻略してみよう！
4ステップで証明できちゃうよ。
さっきの例題をといていこう！
例題
連続する3つの整数の和が3の倍数になる訳を説明しなさい。ただし、整数は正の数とする
ある正の整数を「n」としてみて。
nは「正の整数」だから、
1にもなるし、2にもなるし、10にだってなるんだ。
えっ。なぜ「n」を使わなきゃいけないんだって？！
えっ？
zを使いたい？？
じつは、nは英語の「number (数字)」からきているんだ。
ぶっちゃけzとかqでもいいんだけどさ。
nをつかうとカッコいいじゃん？。
とりえあず正の整数を「n」とおこう！
連続する3つの整数をnであらわそう！
連続する3つの整数ってたとえば、
1, 2, 3
みたいに、1ずつ違う整数のことだ。
たとえば、
1, 4, 5
とかは連続してないね。
だって、1ずつ離れてないし。
nであらわすときは、
連続する3つの整数のうち、正の整数nを、
真ん中の整数
とおくといいよ。
そうすると、
をnで簡単にあらわせるからね。
連続する3つの整数は1ずつ離れてる。
よって、
になるはずだ！
つぎは、連続する3つの整数をたそう。
nであらわした、
をたせばいいんだ。
ぜんぶたしてみると、
(n-1)+n+(n+1)
= 3n
になるね！
最後に、和が「3の倍数」になる証拠をみつけよう。
証拠がみつかれば、
連続する3つの整数の和が「3の倍数」である
って証明できるからね。
例題でいうと、
連続する3つの整数の和は、
3n
になったね。
で、nは正の整数だったよね？？
ってことは、
3n
は3の倍数になるんだ！
だって、「n」には1とか2とか6とかがはいるわけだからね。
そいつらが3倍されたら、
3の倍数になるじゃん？？
だから、連続する3つの整数の和は3の倍数っていえるんだ！
この問題は、
の4ステップで証明できちゃう。どんどんチャレンジして行こう
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。鮭は焼くとうまいね。
数学の先生から、
1から100までの素数を覚えなさい
って言われた？？
えっ。
ふつうにむちゃむちゃ。
だって、1から100までの素数は「25」個もあんだぜ？？
いくらなんでも無理な注文だよ。
しかも数字なんて覚えにくい。
電話番号でギリギリ。
1から100までの素数なんて覚えられねえ。。。
まじ助けて欲しい・・・・・
・・・・・・・・・・・・・
そんなときに役に立つのが「語呂合わせ」というアイテム。
25個の素数をたのしみながら覚えられるんだ。
今日はマイ勉オリジナルの、
1から100までの素数の覚え方がわかる語呂合わせ
を紹介するよ。
よかったら参考にしてみて。
語呂がストーリーになってるよ。
読みながら「1から100までの素数」がおぼえらるはず。
さっそくよんでみよう！
兄さんと午後にセブンイレブンにいってみた。。
2, 3 5, 7, 11
意味もなく、ブラブラしてみたけど、誰もいないじゃん。
13, 17
暇すぎるから、塾で勉強しようかと思ったぐらいだよ。
19
そしたらさ！
兄さんがおれの肉まん食べちゃったんだよ。
23, 29
もうケンカだよ、ケンカ。
しかも、
肉まんだけじゃない。
サーティーワンアイスまでみな食べちゃったんだよ。
31, 37
もう、信じられる？？？
よい子のふりして立ち読みしてる場合じゃなかった！
41, 43
しかも兄さん、
しなっとしたゴミ袋おれにわたしてさ、
47, 53
「ご苦労さん」
59
っていったんだ。
ふざけんな！
おれに肉まんとアイス買ってよ！！泣
無意味にむなしいだけじゃん！
61, 67
財布もってないんだよ。
71
これじゃあ、
牛丼の並み盛りも食えねえよ。
73
もう、
泣くしかないぜ。
79
もうわかった。
いいよ、兄さん。
くれぐれも、
ヤーさん・ヤクザの急な絡みに気をつけてね。
83, 89, 97
・・・・・・・・・・・
と以上が語呂合わせだ。
最後はミステリアスな展開になったね。
ストーリーをおさらいして、
1から100までの素数をおぼえてみよう！
1から100までの素数？？
そんなの語呂で一発さ。
25個もあるけど大丈夫。
どうしようもない兄弟ケンカの物語を思い浮かべればいいんだ。
がんばって暗記してみよう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。腸の調子がいいね。
中3数学では、
素数（そすう）
を勉強していくよ。
いままで、
整数とか、自然数とか、約数とか、公倍数とか、最小公倍数とか・・・・
いろいろな数をならってきたね。
だけど・・・・
素数なんて一度も聞いたことがない！
って驚いてると思うんだ。
だから今日は、
「素数とは何か」をわかりやすく解説してみたよ。
よかったら参考にしてみて。
〜もくじ〜
素数をWikipediaでしらべてみると、
正の約数が 1 と自分自身のみである自然数で、1 でない数のこと
ってかいてあるね。
ちょっとよくわからない！？ うん、ちょっとむずい。
もっと簡単にいってやると、
「1」と「自分」でしか割り切れない自然数のこと
だよ。
えっ。
まだピンときてないだって！？？
そうだね。
素数の具体例をみていこう！
いきなりだけど、数字の「5」をイメージしてほしい。
そうそう。
よくある数字の5だよ。
じつは「5」は素数なんだ。
なぜなら、
1
と
5（自分）
でしか割り切れないからね。
あっ、自然数の割り算に限定したときね。;
2で割っても余り1になっちゃう。
3で割っても余りが2になっちゃう。
4でも無理ゲーだね。
「5」を割り切れる自然数は、
「1」と「5（自分）」しかない。
うん、ないない。
だから、
「5」は「素数」といえるんだ！
つぎはそのお隣の、
6
をみてみよう。
「6」という自然数は、
素数じゃない
んだ。
なぜなら、
1と自分（6）以外の自然数でも割り切れちゃうからね。
2でも割り切れちゃうし、
3でも割り切れる。
よゆーで、
「1と自分以外の自然数」でわりきれちゃうじゃん。
だから、「6」は素数ではないんだ。
どう？？納得したかな？？
雰囲気的に、
1は素数なのかも・・・・
って思っちゃうかもしれない。
だって、「1」と「自分（1）」で割り切れちゃってるし。
だけど、覚えておいてほしいのは、
「1」は素数でもなんでもない
ってこと。
これだけはおさえておこう。
なんだろうな、そういうものだと思っちゃおう。
星は夜空に輝くものだとか、
熊はほ乳類だとか、
週刊少年ジャンプは面白いだとか・・・
みたいな感じでそういうものだと思おう。
えっ。
納得しないだって？！
どっからどう見ても1が素数にみれるって？？
うーん、そうだな。
こう覚えてみたら？？
素数とは、
「1」と「自分」でしか割り切れない自然数で、
「1」と「自分」はいっしょになっちゃいけない
ってね。
こう覚えておけば、1が素数じゃない気がしてくる。
なぜなら、
1にとっての「自分」は「1」だからね。
とにかく。
「1」は素数じゃない
っておぼえておこう！！
素数とは何かをここまで解説してきたね。
どう？？納得したかな？？
数学を勉強していて、
あれ・・・素数ってなんだろう・・・？？
って思ったらちょっとストップ。
基本を復習してみよう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。チーズとバターは紙一重だね。
中3数学を勉強してると、
因数（いんすう）
ってでてくるね？？
小学校の算数じゃきいたことない。
友だちと因数について話すチャンスもない。
うん、むずかしそうだし、よくわからない。。
そこで今日は、中3数学でスタートダッシュをきるためにも、
因数とはなにか？？
を解説してみたよ。
よかったら参考にしてみて。
因数とはずばり、
ある数・文字式を、あえてかけ算であらわしたときに、
かけられている数・文字式のこと
だよ。
えっ。ぜんぜん意味がわからないだって？！？
そうだね。
因数の具体例をみていこう！
文字と数にわけて考えてみたよ。
まずは「数」の因数の例だね。
そうだなあ、たとえば、
21
っていう自然数をイメージしてみて。
あえて。
あえて、かけ算の形になおしてみると、
7×3
にできるよね？？？
だって、「さんしちにじゅういち」だからさ。
ある数をかけ算になおしたとき、
かけられているものを「因数」というんだったね？？
ってことは、21の因数は、
だ。
どう？？
ちょっと因数に近づけたかな？？？
つぎは「文字式」の因数の例だね。
例として、
a² – a
をイメージしてみて。
この文字式もあえて、
あえて、かけ算になおしてみるんだ。
aで（）でくくってやると、
a × (a – 1)
っていうかけ算になるよね。
かけ算になおしたときに、かけられているやつが「因数」。
よって、a² – aの因数は、
の2つになるんだ。
どう？？
文字式の場合もしっくりきた？？
因数とはなんだろう？？
そう感じたらまず、
数や文字式を「かけ算」になおしてみよう！
そうすれば因数がでてくるはずだ。
がんばって探してみてね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。シロップに要注意だね。
中学数学でならう公式は3つある。
ぶっちゃけ公式覚えてれば大丈夫。
もうね、楽勝。
公式通りに計算すればいいからね。
だけどさ、
乗法公式はなんでつかえるんだろう？？
ぶっちゃけ怪しいんだよね。
知らないおじさんについていくみたいでさ。
そんな疑問を解消するために今日は、
乗法公式（式の展開の公式）はなぜつかえるのか？？
を解説していくよ。
よかったら参考にしてみてね。
式の展開の公式を証明するために使うのはただ1つ。
それは、
さ。
えっ。分配法則なんて忘れただって？？
そうだね。
分配法則とはずばり、
（）の外側の数字や文字を（）内の項に順番にかけて展開すること
だよ。
たとえば、
(a+b)(c+d)
っていう計算式があったとしよう。
分配法則つかえば一瞬で展開できるんだ。
まず、「a」をうしろにある（）内の項にそれぞれかける。
そして、たす。
(a+b)(c+d)
＝ ac + ad
つぎは「b」をうしろの（）内の項にかけて、たしてやるんだ。
つまり、
「b」を「c」と「d」にかけてたせばいいのさ。
よって、
(a+b)(c+d)
＝ ac + ad +bc + bd
になるね。
この分配法則が使えればOK。
乗法公式も証明できちゃうよ。
さっそく一つ目の、
(x+a)(x+b)
を証明してみよう。
分配法則で展開してやればいい。
まず、「x」をうしろの（）の2つの中にかける。
(x+a)(x+b)
= x^2 + bx
つぎは、「a」をうしろの2つの項にかけてたしてやる。
すると、
(x+a)(x+b)
=x^2 + bx +ax +ab
になるね。
あとは同類項「bx」、「ax」をまとめるだけさ。
(x+a)(x+b)
= x^2 + bx +ax +ab
= x^2 +(a+b)x + ab
すると、乗法公式のできあがり！
いっちょ上がりさ。
つぎは平方の公式の証明だね。
こいつも分配法則で証明できちゃう。
まず、(a+b)^2をかけ算になおしてみよう。
すると、
(a+b)^2
= (a+b)(a+b)
になるね。
これをさっきみたいに分配法則で展開してみよう。
まず、いちばん左の「a」を後ろの「a」と「b」にかける。
そして、たす。
(a+b)^2
= (a+b)(a+b)
= a^2 + ab
つぎは、「b」を後ろの「a」と「b」にかける。
そして、たす。
(a+b)^2
= (a+b)(a+b)
= a^2 + ab + ab + b^2
あとは同類項をまとめるだけ。
すると、
(a+b)^2
= (a+b)(a+b)
= a^2 + ab + ab + b^2
= a^2 + 2ab + b^2
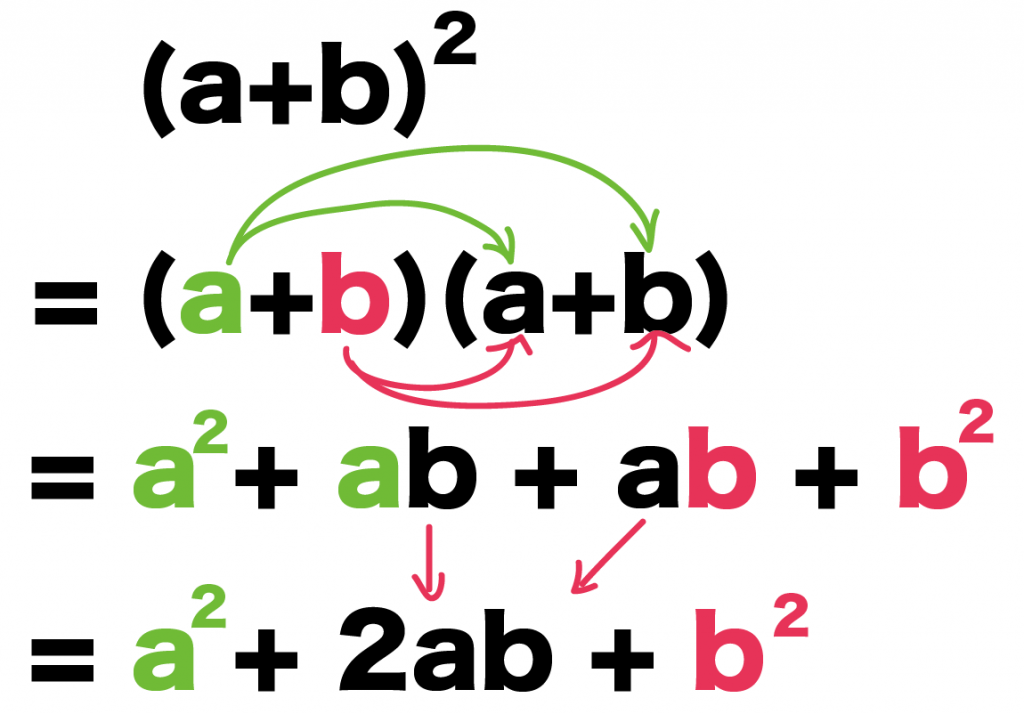
あら。
平方の公式のできあがり！
いよいよ「和と差の積」の公式の証明だ。
こいつも分配法則で一発。
まず、いちばん左のaを右の（）内の項にかける。
そして、たす。
(a +b) (a-b)
= a^2 – ab
2つめの「b」を後ろの（）にかけてやると、
(a +b) (a-b)
= a^2 – ab +ab -b^2
になるね。
あとは同類項をまとめてやろう。
の2つだね。
こいつらをたして消してやると、
ほら！
乗法の公式の「和と差の積」のできがあがり。
乗法公式を覚えることは大切。
だけど、
テストで忘れたら危機。危機におちいる。
だからこそ、
なぜ乗法公式がつかえるのか？？
ってとこまでおさえておこう。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。カフェはやっぱいいね。
中学2年生になると、
二元一次方程式
を勉強するよね？？
正直、聞いただけでもむずかしそうだし、数学が嫌いになっちゃいそうだ。
いや。
いやいや。
大丈夫。
そんなときはこの記事を読んでみて。
二元一次方程式の意味がしっくりするはずさ。
〜もくじ〜
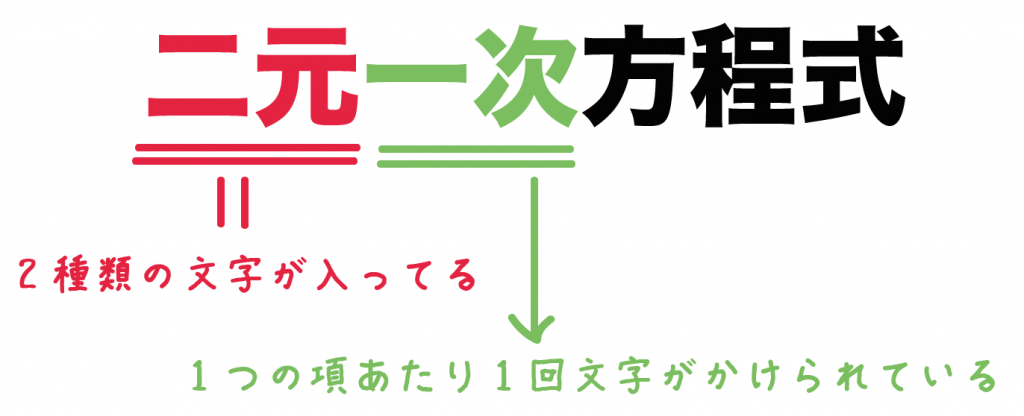
二元一次方程式って、
2種類の文字が使われている一次方程式のこと
なんだ。
もっと簡単にいうと、
2種類の文字が入っていて、1つの項あたり最大1回文字がかけられている方程式
のことなんだ。
たとえば、
2x – 5y = 26
とかね。
この方程式は、
xとyの「2種類」の文字が使われていて、
なおかつ、
1つの項に1回ずつ以下ずつ文字がかけられているからね。
じつは、
ってことを表しているんだ。
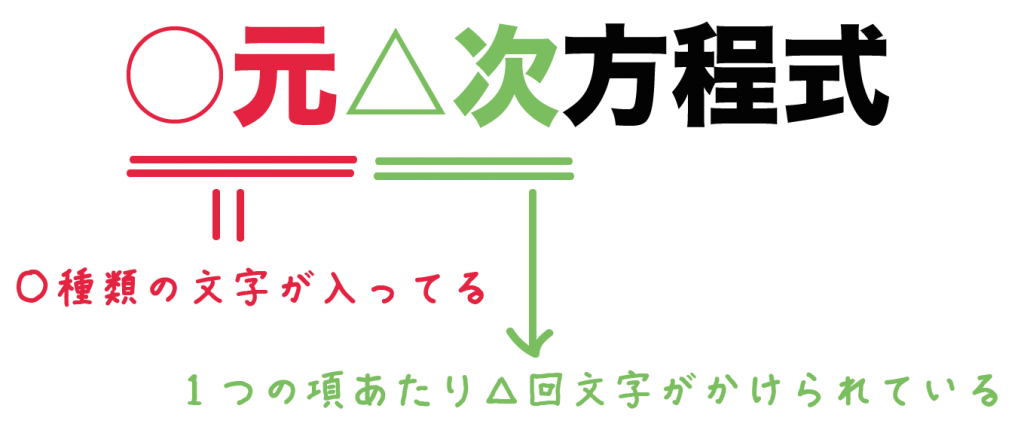
だから、
x + y + z = 90
っていう方程式は「三元一次方程式」だし、
2x + xy + z^4 – w = 90
っていう方程式は「四元四次方程式」になるのさ。
数学の先生に、
この方程式は何元何次方程式ですか？？
ってきかれたら、
ということを見極めよう。
即答できればクラスの人気者さ！
二元一次方程式にも「解」があるよ。
方程式の「解」って、
文字に入れても等式が成り立つ「数字」のこと
だったよね。
たとえば、さっきの「2x-5y = 26」という二元一次方程式の解は、
・・・・・・・・・
などなど・・・2つ以上あるよね。
どうしよう・・！
解が1つじゃねえよ・・・・
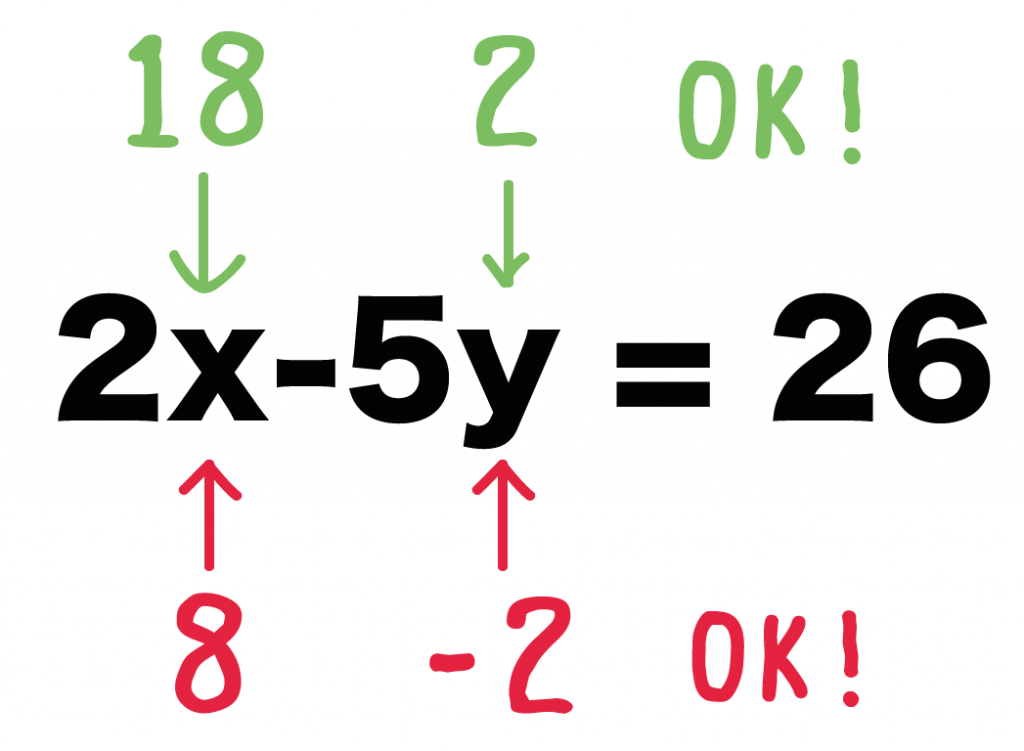
じつは、二元一次方程式1つだけでは解が1つに定まらないんだ。
二元一次方程式の解を求めるには、
2つ以上の二元一次方程式が必要だよ。
たとえば、
っていう2つの方程式があったら、
さっきの2つの解のうち、
しか成り立たなくなるよ。
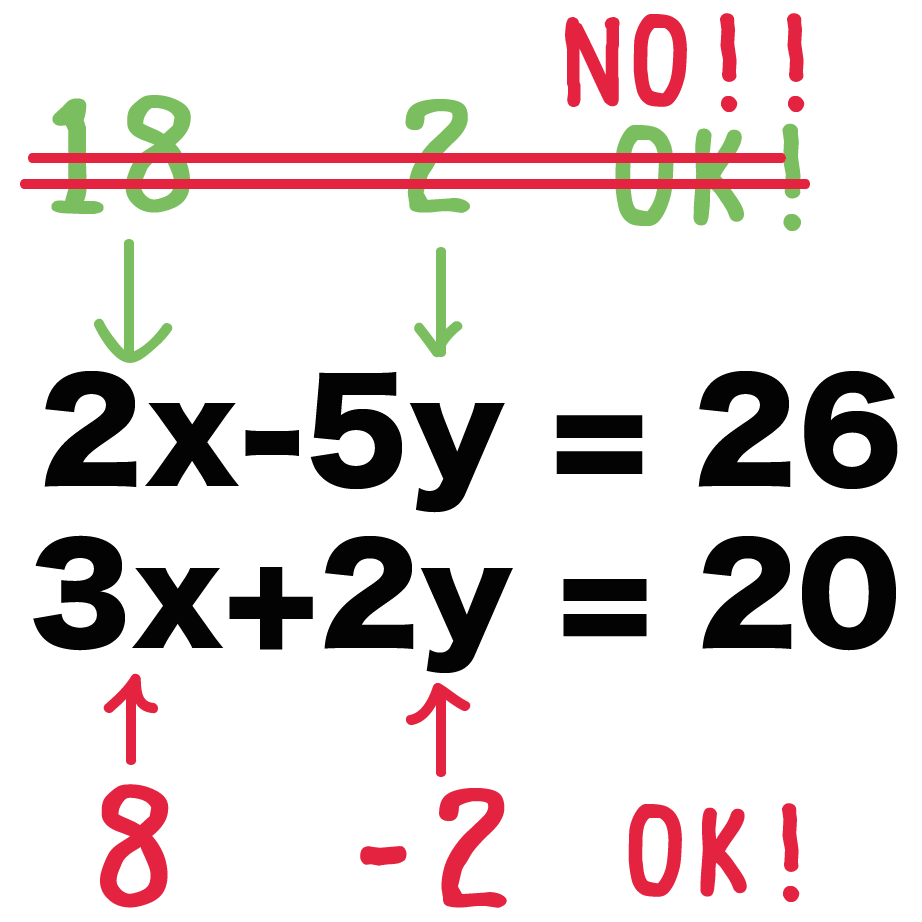
ってことで、
二元一次方程式の解を1つに決めたかったら、
2つの二元一次方程式を用意する
ってことをおぼえておこう。
このように、2つの方程式を組にしたものを「連立方程式」っていうんだ。
これから連立方程式をみっちり勉強していくよー！。
二元一次方程式って呪文みたいに聞こえるけど、
じつはシンプル。
2種類の文字が入った一次方程式のことなんだ。
もっと簡単にいってしまえば、
2種類の文字が入っていて、1つの項あたり最大1回文字がかけらている方程式
のことなんだ。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。家具の匂いが好きだね。
文字式の計算でいちばんむずかしいことって、
分数の通分
だよね。
分数だけでヤッカイなのに、それが文字になる？！？
たまったもんじゃない。
そこで今日は、
分数の文字式の通分方法
を3分で解説するよ。
通分がどうしてもできねえ！ってときに参考にしてみて。
〜もくじ〜
文字式の分数の通分方法を勉強する前に、
分数の通分ってなに？？
ということを確認しよう。
これがわかってないと文字式の通分どころじゃないからね。
通分って、
2つ以上の「分母の違う分数」を1つにすること
なんだ。
これが分数の通分っていうものさ。
たとえば、
1/2 + 1/3
っていう分数式を通分して1つにしてやると、
5/6
になるんだ。
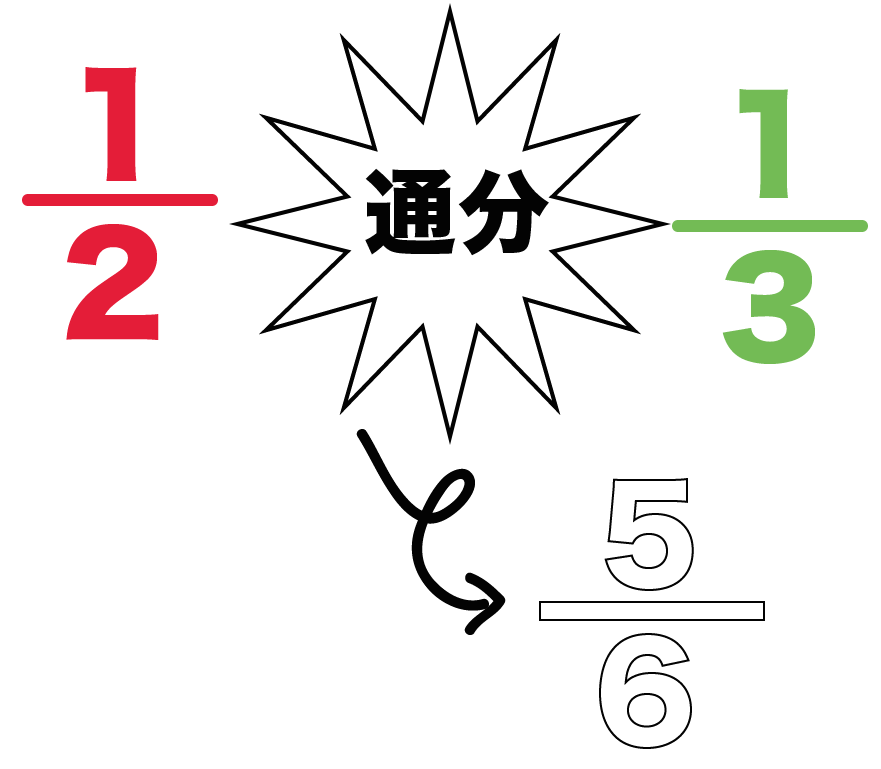
これを文字式の分数でもやっていくってわけさ。
分数の文字式を通分する方法は、
っていう2ステップだ。
分子と分母を順番に計算すればいいってことだね。
つぎの例題をときながら通分をマスターしていこう！
つぎの分数の文字式を通分して1つにしなさい。
2b/a – 5d/c
まずは通分後の分母をきめちゃおう。
通分後の分母は、
分母をかけあわせたもの
なんだ。
例題の計算式の2つの分母は、
だったよね？？
こいつらをかけあわせてやればいいんだ。
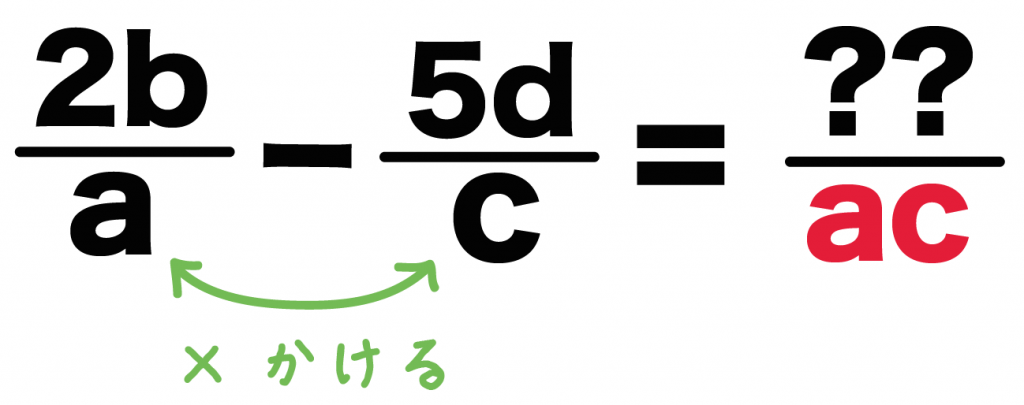
その答えが通分した分母になるってわけ！
あとは分子だ！
通分後の分子の計算方法は、
たすきがけ
というものさ。
「自分の分母」と「相手の分子」をかけたものを足し合わせればいいんだ。
ななめに掛け合わせるようすが「駅伝のたすき」に似てるから、
「たすきがけ」って呼ばれているんだ。
例題でいうと、
っていう計算をして、そいつらを足してやればいいんだ。
足したものが通分後の「分子」になるのさ。
それぞれ計算してやると、
になる。そんで、そいつらをたしあわせてやると、
2cd-5ad
になるよね。こいつが通分後の分子になるわけさ。
ってことで、
最終的に例題の分数を通分すると、
(2bc-5ad)/ac
になるよー！
おめでとう。 これで文字式の分数の通分もマスターできたね！
分数の文字式の通分はどうだったかな？？
っていう2ステップで簡単に計算できちゃうはず。
中学数学の基礎だから、ここでマスターしておこうね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。10円玉募金をはじめたね。
分数がふくまれる「等式の変形」ってむずかしいよね。
整数だけでもヤッカイなのに、分数がはいったらもっとヤバい。
そこで今日は、
「分数がふくまれている等式の解き方」をわかりやすく解説していくよ。
分数がふくまれる「等式の変形」には2つのパターンがあるんだ。
まず1つ目は分母を払うパターンだ。
これは「求める文字」が分子にあるタイプだね。
たとえば、
つぎの等式をaについて解きなさい。
a/2 + b/5 = 2
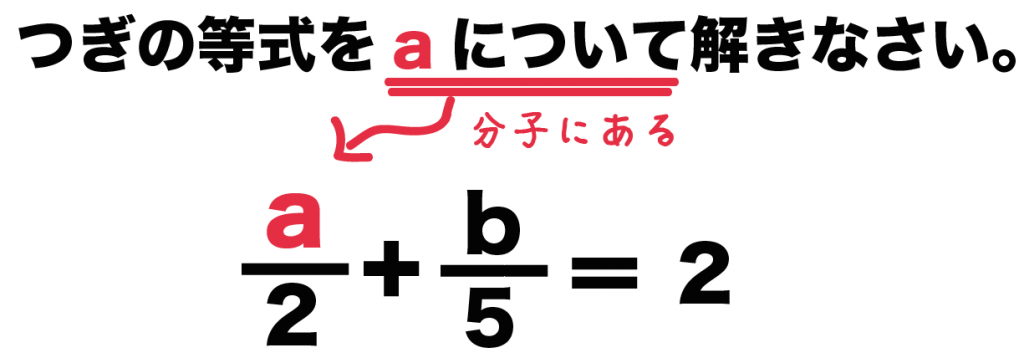
っていう問題だ。
これは、
○○について解きなさい
っていう○○の文字が分子にはいっているよね。
このタイプの問題はつぎの3ステップでとけちゃうんだ。
まず分母をはらっちゃおう。
等式から分数を消せちゃうってわけ。
つまり、
分母の最小公倍数を等式全体にかけてやればいいのさ。
例題でいうと、
分母の「2」と「5」の最小公倍数は「10」だよね。
こいつを等式の両辺にかけてみると、
10×(a/2 + b/5) = 2 × 10
5a + 2b = 20
になるね！
分母をはらった？？
そのつぎは移項だね。
「求めたい文字」を左辺に移動させよう！
それ以外は反対の右辺におしこんでね。
例題でいうと、
等式で求める文字は「a」だったよね？？
ってことは「a」をふくむ項を左に、ソレ以外の項を右によせてやろう！
すると、
5a + 2b = 20
5a = 20 -2b
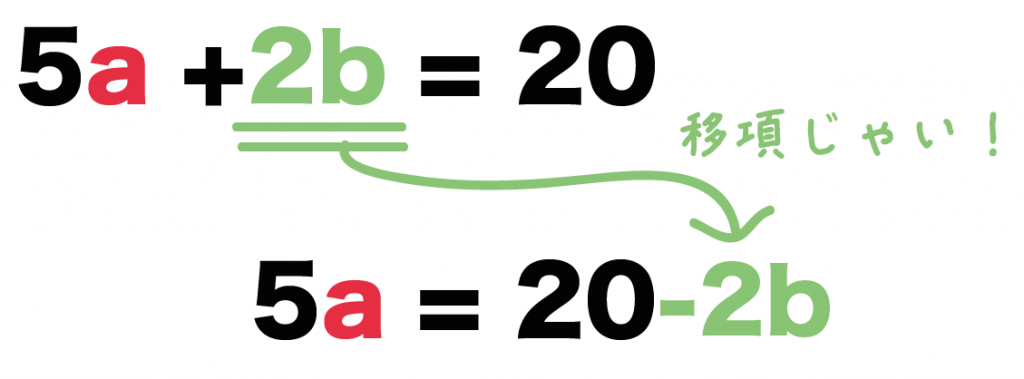
になるね！
移項するときに、項の符号が変わることに注意してね。
最後は「求める文字」の係数をとってあげよう！
求める文字の前についている「数字」が係数だよ。
こいつで両辺をわってあげよう！
すると例題の式は、
5a ÷ 5 = (20-2b) ÷5
a = (20-2b)/5
になるね！
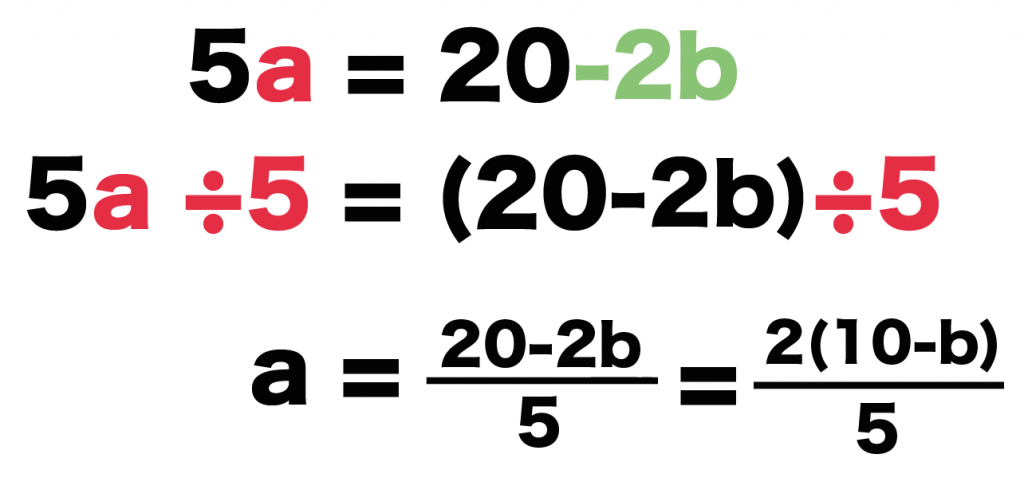
これで分母をはらうやり方はオッケーだね！！
等式の変形の2つ目のパターンは、
「求める文字」が分母にある場合だ。
たとえば次の問題のように、
つぎの等式をaについて解きなさい。
1/a + 1/b = 1/c
「〜について解きなさい」の「〜」が分母にはいっちゃっているパターンだ。
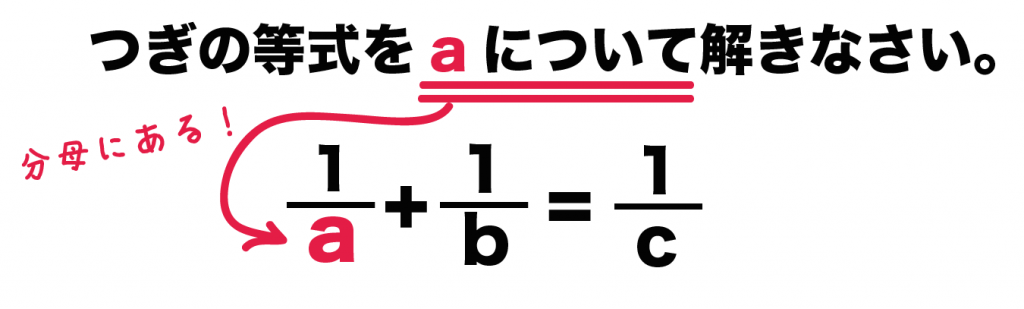
このタイプはつぎの3ステップでとけちゃうよ。
「求める文字」を左辺に、ソレ以外の項を右辺によせちゃおう！
符号に注意して移項しちゃってくれ！
例題の等式では「a」が求める文字だったよね？
だから「a」を左辺に、ソレ以外の項たちを右辺によせてみよう。
すると、
1/a = 1/c -1/b
になるね！
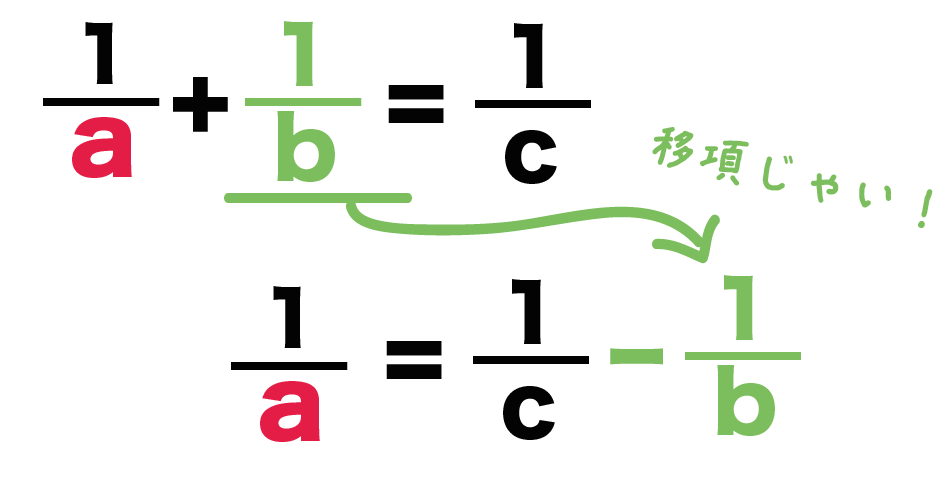
右辺を通分して1つの分数にしてみよう！！
例題でいうと、
1/c -1/b
っていう右辺を通分してやればいいんだね。
えっ。通分のやり方がわからない！？
そんなときは「分数をふくむ文字式の通分方法」を復習してみてね。
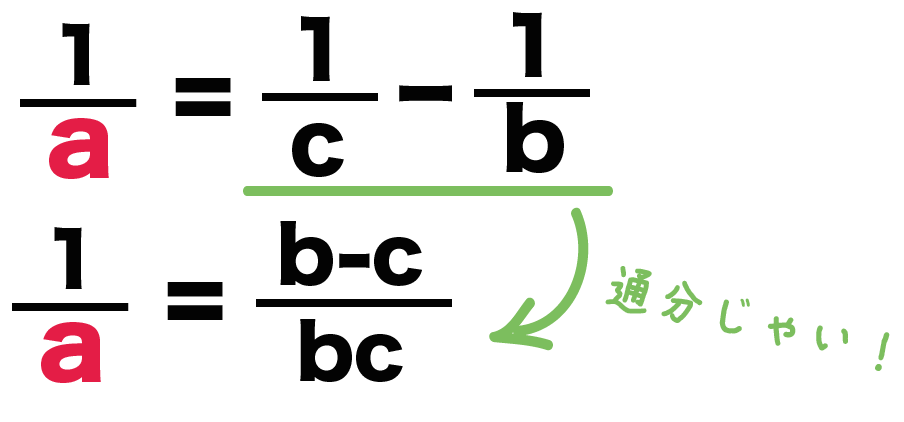
通分してやると、
(b-c)/bc
になるね！
いよいよ最後のステップ。
両辺の分数を逆数にしてあげよう！！
左辺と右辺はそれぞれ1つの分数になっているから、
分子と分母を入れ替えてやればいいのさ。
例題でいうと、
1/a = (b-c)/bc
a = bc/(b-c)
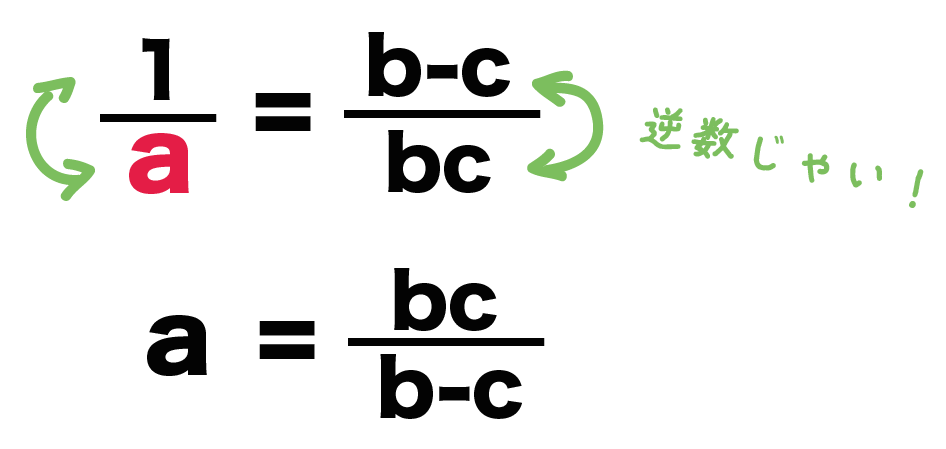
になるね！
これで「通分するパターン」の解き方もマスターしたね。
おめでとう！
分数がふくまれている等式の変形のやり方はどうだった？？
をマスターしておけば大丈夫。
きっとテストでいい点とれるはず！本番前によーく復習しておいてね。
そんじゃねー
Ken
文字式の表し方をしっかり勉強しましたね？？
次はいよいよ文字式の計算問題に挑んで行きます。「文字式の計算問題」と聞くと難しく聞こえますよね？？
す、数字だけの計算はもはや通じない。ど、どうしよう、、中間テストが迫ってきている・・・・・
そんな危機的な中学生の方のために、
【中1数学】文字式の計算問題の解き方に関する3つのコツ
という記事を書きました。
文字式の計算問題の解き方をまったく知らない？？ そんな中学生でも1秒で問題をとける方法です。中学校のテストで死にそうになってるときに参考にしてみてください。
さっそく「文字式の計算問題の解き方」のコツを紹介していきます。
文字式の計算問題の解き方は、以下の原則が大前提になっています。それは、
掛け算 → 足し算
です。
これは正負の四則演算でも同じでしたね。文字式でもこの原則は一緒！！
「掛け算」を計算してから「足し算」を片付けるようにしましょう。
それでは、文字式の計算問題を瞬殺するための3つのステップをみていきます。
文字式の計算では最初に「掛け算記号×」と「割り算記号÷」を消し去っちゃいましょう。
文字式の表し方で、
文字式では「×」と「÷」の演算記号を省略するぜ！
ということを勉強しましたね？？ ところが、文字式の計算問題の中には「×」と「÷」が省略されていない文字式もあります。たとえば、
という文字式の計算問題。こういうときは「÷」記号を消し去ることが大切。つまり、割り算の計算をしてしまうということです。
「×」や「÷」の計算記号を残したままでは文字式の計算問題を解いたことになりません。テストで100点をとるためには「×」と「÷」を消去する文字式の解き方を覚えておきましょう。
次に、文字式の計算問題の「カッコ（）」を消しちゃいましょう！
えっ。文字式の問題でカッコ（）のはずし方がわからないですって！？？ あ、そういうときは、
分配法則
を使えばいいんです。詳しくは【中学数学】分配法則のチョー便利な1つの使い方を参考にしてくださいね。分配法則とはカンタンに言ってしまえば、「カッコのをはずしたる」ということです。
文字式の計算問題の例をみてみましょう。
たとえば、
という文字式の計算問題があったとしましょう。この文字式には「3」という数字がカッコ（）の前についています。分配法則をつかってカッコ（）をはずしちゃいましょう！
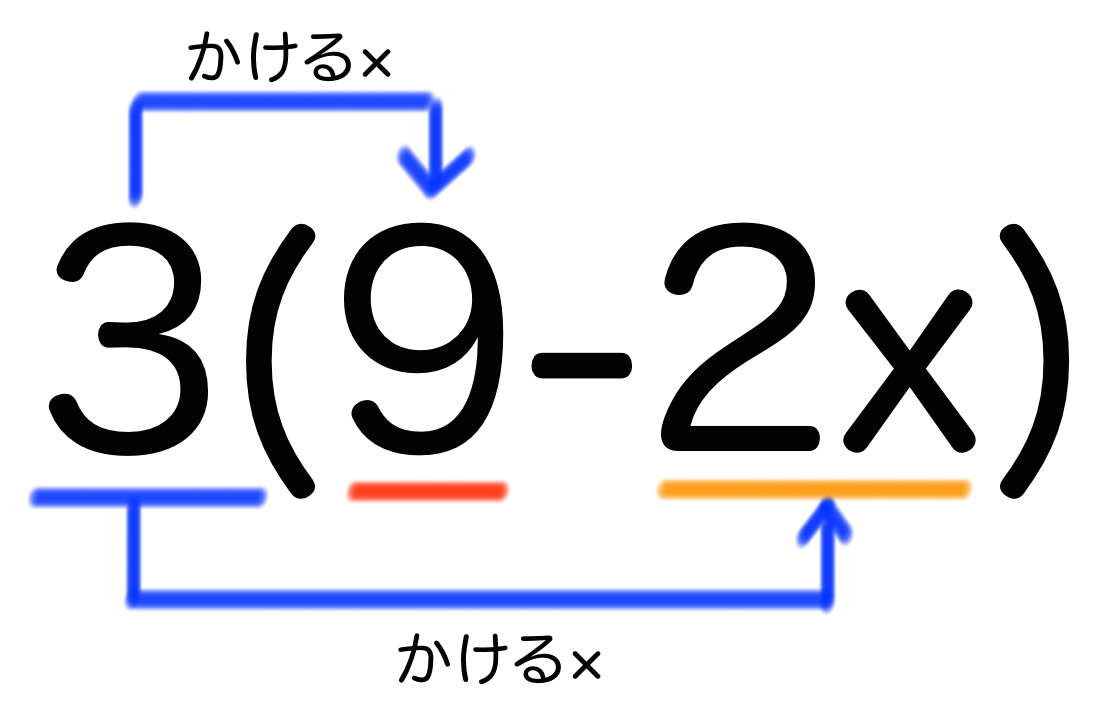
すると、
となります。
カッコ（）がついている文字式の問題は分配法則でスッキリしちゃいましょう！
ここで注意することは、
カッコの外の数字がマイナスの計算問題
です。
正しい答えはカッコ内の2つの項に「-3」を等しく掛けた
いよいよ文字式の計算の最後のステップです。
「掛け算×」も「割り算÷」もなし！
「カッコ（）」もなし！！
これだけでは文字式の計算は終わりません。そのあとに、
同じ文字の項をまとめる！
という作業が残っています。これはいったいどういうことなんでしょうか？？？ 文字式の例題で確認してみましょう。
たとえば、4(2x-5)-3(9-2x)という文字式の計算問題があったとします。
さっきとりあげたステップのうちの2つ目の「カッコ（）をはずす」という解き方を適用すると、
4(2x-5)-3(9-2x)=8x-20-27+6x
となります。ここで最後のステップ「同じ文字同士をまとめる！」という計算をしてみましょう。この式には「x」と「数字」という2種類の文字が存在します。これらをまとめてやると、
8x-20-27+6x=14x-47となります。
同じ種類の文字・数字をまとめてようやく「文字式の計算問題を瞬殺した」と胸を張れます。
最後まで気を抜かないで文字式を計算してやりましょう！！
以上の3つのステップを踏めば、文字式の計算問題をたぶんおそらく3秒ぐらいで瞬殺できるはずです！！
文字式の計算に時間がかかりすぎるという悩みをかかえている中学生は参考にしてみくださいね！
それでは、また今度です。
Ken
中学1年生の数学単元で「一次式」と「二次式」という言葉が登場します。
一次式とか二次式とか聞こえはかっこいい。ガンダムのパイロットが使ってそうな数学用語ですよね？？ 「こちら、司令室。一次式、二次式、ともに完了。ラジャー」みたいな感じで。
ところが、です。
ぶっちゃけ、ぶっちゃけ、です。
中学1年の数学で「一次式」について勉強したけどよくわからない！一次式の説明文を何度読み返してもわからない！！どうしよう！
困ったので数学の教科書を読んでみると、
項
のように、文字が1つだけの項を1次の項といいます。また、1次の項だけの式、または、1次の項と数の項の和で表される式を一次式といいます。
という説明が書いてあります。
塾で予習していた中学生ならばこの問題に即答できるかもしれません。
ただ、数学の授業ではじめて「一次式」を勉強する方にはよくわかりませんよね？？ 一次式を理解できなければ二次式もわからずにゲームオーバーになってしまいます。
そこで今日は、
次数の意味から5分でわかる！一次式と二次式の違い
という記事を書いてみました。一次式と二次式の違いにピンと来ていない中学生の方！よかったら参考にしてみてください。
以下が記事のもくじです。
それではさっそく確認してみましょう。
一次式と二次式の違いを理解するために必要なこと。それは、
次数とは何か？！？
を知っておくことです。「次数」の意味がわからないと、一次式や二次式の違いがスッキリしません。っということで、まずは次数の意味を確認していきましょう。
次数とは、
項に文字が掛けられている数
を意味します。たとえば、
2つ目の項である「-b」はどうなるでしょう？？ これは
掛けられた文字の数は「1つ」ですよね？？ つまり、この項の次数は一次となります。
同様に、最後の項「9」をみていきましょう。この項には数字しかありません。どこをどう探しても文字が見当たりませんね？？ こういう場合の次数は「0」になります。文字がない数字だけの項の次数は「0」になることを頭にいれておきましょう。
さて、一次式と二次式の基礎である「次数」の解説は終了しました。次数を理解しちゃえば一次式も二次式もひとひねり。
超ラクショーです。
一次式とは「一番大きい次数が一次である文字式」のことです。ここでは「一番大きい」ということに注目してください。次数の合計ではなく最大の次数に注目することがポイント。
たとえば先ほどの文字式にちょっと似ている
すると、
けっして、
という間違えをしないようにしましょう。
一次式を理解しちゃえば二次式もわかったようなもんです。
二次式とは「一番大きい次数が二次である文字式」のこと。一次式との違いは「一番大きい次数が二次」という箇所だけです。
一番最初に例としてあげた
3つの項の中で一番大きい次数を持つのは
以上で一次式と二次式の見分け方の解説は終了です。
一次式と二次式を見分ける際にもっとも重要なのは、
文字式で一番大きい次数を持つ項をさがす
という作業です。これが瞬時にできるなら大丈夫。一次式だろうが二次式だろうが三次式だろうが見分けることができます。
それでは、また今度です。
Ken
中学数学で文字式を勉強していると、
「項と係数」
という新しい数学用語が登場します。これはいったい何ものなのでしょうか？？
項と係数の違いを確認して数学のテストでいい点数をとっちゃいましょう。
この「項と係数」という新しい数学用語の理解を深めるため、まずは文字式に注目しちゃいましょう。
文字式とは以下の3つの要素でなりたっています。
文字式にふくまれる要素のうち、
+に挟まれた数字や文字
を「項」といいます。
たとえば、
2-8+7
という式があったとしましょう。
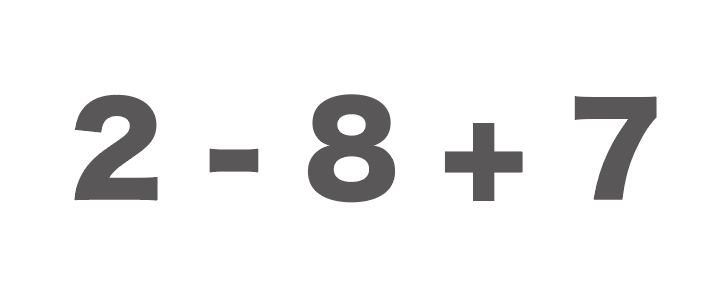
これをいったん、＋だけの式に直すと、
2+(-8)+7
になりますね？ 「＋に挟まれた数字や文字」が項なのでこの場合だと、
が項になります。
「項」についてもっと理解を深めたい！
という方は「項の意味を100%理解できる方法」という記事を読んでみてくださいね。
さて、項の正体はわかりましたね？？
それでは次に「係数とは何か」を確認していきましょう。
係数とはカンタンにいってしまえば、
文字の前についている数字のこと
です。さっきの文字式から2aという項を例にとりましょう。
文字式における1つの項は、
の2つの要素で成り立っています。文字式の文字についている数字が「係数」なわけです。見た目からも係数の意味からもわかりやすいですよね？？
ふう！項と係数は楽勝でしたね！？
それでは、また今度です＾＾
・・・・・・・
といいたいところですが、項と係数には2つだけ注意する点があるのです。これを最後に確認してみてください。
文字式の項において、文字の前に数字がないとき。たとえば、
この場合、文字の前に数字がないのでaとbの項の係数は「0」ではないかと疑ってしまいます。ふつうに考えたらこうなります。
じつは、文字の前に数字がない項の係数は「1」なんです。
これをしっかりと覚えてください。文字式の表し方のルールで確認したとおり、
文字に1がかかっている場合は1を省略しましたよね？？
そのため、係数がゼロのようにみえてもきちんと「1」が係数としてかかっているのです。
見えない「1」という係数に注意しましょう。
分数の係数にも注意が必要です。
とくに分子に文字、分母に数字という文字式がけっこうやっかいなんです。
たとえば、
xの係数を求めて？？
と言われたら何て答えます？？
これまでの係数に忠実にしたがえば、
xの前に数字がついてないから係数は1じゃないの？！？
という答えが飛び出してきそうです。だがしかし、この答案はとんでもなく間違っています。
間違えを防ぐためにも、
分数を含む項では、分子から文字をいったんおろして考えてください。
先ほどの
としてやります。すると、
となります。よーーく見てみると
つまり、
それでは、また今度です。
Ken
中学1年数学で勉強する「式の値」の解き方がよくわからない。
そんな声をよく耳にします。式の値とか急に言われてもピンと来ないし、いくら想像してもいったいどんなモンスターなのか検討もつきません。
できれば「式の値」という中1数学の単元をスキップしたいですよね？？難しい数学の単元なんてお断りしたいです。
だがしかし、です。
「式の値の解き方」を知らずに中間・期末テストを迎えるとテストで確実に爆死します。
中学数学でいい成績をとっておきたい。
そんな目標を持っていたら「式の値の解き方」をマスターしておきましょう。この記事では以下の順番で式の値を解説していきます。
式の値の解き方を勉強すれば、中間テストの数学でいい点数をとれること間違いなしです！！
それでは、さっそく見て行きますよー
式の値とはいったいどこの何者でしょうか？？？
名前を見る限りむずかしくて気難しいヤツにみえます。だがしかし、中1で勉強する式の値はいたってシンプルな内容なんです。
式の値とはずばり、
文字式の文字に数字を当てはめたときの値
のことです。
「文字式の文字に数字を当てはめたときの値」=「式の値」
というわけですね？？ なるほど、ただの省略形だったわけですね。
中学の数学では「文字に数字を当てはめる」作業のことを「代入」、当てはめる数のことを「文字の値」と呼んでいます。
式の値の具体例をみていきましょう。たとえば、次のような文字式
があったとしましょう。これはある中学生のひと月のお小遣いの状態を表しています。xという文字は「洗った皿の枚数」です。つまり、1枚お皿を洗うという家事の手伝いをすると40円お小遣いが増えるというわけです。
今月は皿洗いに力を注いだので43枚の皿を洗う事に成功しました。すると、この中学生の今月のお小遣いは、
と計算できますよね？？
このときの「文字mに43を入れること」を「代入する」といい、文字式に代入する「43」を「文字の値」と呼んでいるんです。
それで、文字式にある数字（文字の値）を代入して求めることができた値を「式の値」と呼んでいます。
上の例でいえば、m（皿を洗った枚数）に43を代入した結果得られる「2220」がこの文字式の「式の値」というわけです。もうおわかりですね？？
まとめると、
式の値とは、文字式に数字をぶちこんだときの計算結果
ということになります。
式の計算は思ったよりカンタンでしたね？？？
文字式の文字に数字をぶちこんでやるだけです。その結果得られる数字を「式の値」と呼んでいるわけです。
ただ、「式の値」の問題の解き方にはある1つのコツがあります。
それは、
あせらずにゆっくり式の値を求める
ということです。ものすごく当たり前のこといっていますね。 ただ、式の値を求める計算問題では焦るとミスしてしまうことがあるのです。
したがって、
式の値の問題では計算過程をはぶかずにすべて書くことをおすすめします。
なぜなら、マイナスの符号が絡んだ「式の値の計算」ではミスが出やすいからです。
たとえば、
のとき、次の式の値を5秒で求めなさい
という式の値の問題があったとしましょう。このとき、
式の値？？ はあ？カンタンだよ、文字に数字を入れるだけやろ？！
といきり立っていきなり答えを書き込んではいけません。計算ミスを防ぐために文字に数字を代入する計算過程を丁寧に書いてみましょう。
先の例で言えば、
という感じで式の値を算出する計算過程を書いておく。これにより−の符号関連の計算ミスを最小限にとどめることができます。
計算過程を書くなんて正直だるいですよね？？
ただ、数学のテストでケアレスミスをなくすために途中の計算式を書いた方がいいんです。決して答えを急いではいけません。
ゆっくりと慎重に式の値を計算する。
これが唯一の式の値の解き方のコツです。テスト時間に余裕がある限りなるべくゆっくり計算問題をといてみてください。
式の値の解き方はいかがだったでしょうか？？
「式の値」とか名前はクールですがあまり大したことありまえせんでしたね？？。
式の値の計算問題でいつもミスをする！そもそも式の値の意味がわからない！！
そんな中学生の助けになったら嬉しいです。
それでは、また今度です！
Ken Sawai
