こんにちは!この記事をかいているKenだよ。鮭を2匹やいたね。
正三角形を作図したい。
そんなときってたまに、ある。
宿題にでてしまったり、
正三角形を落書きしたくなったりしたときにね。

今日はそんな身近な、
正三角形の書き方・作図方法を3ステップで解説していくよ。
よかったら参考にしてみて。
使うものは「コンパス」と「定規」。
こいつらがあれば、
どんな正三角形だってかくことができる。
むちゃキレイにね。
今回はいっしょに、
1辺が6cm の正三角形ABCをかいていこう!
書き方はつぎの3ステップさ。
まず使うのは、
定規、きみだ。
定規をつかって、
正三角形の1辺をひいてみよう。
定規に沿って、
すーーーっと線をかくだけでいいんだ。
1辺が6cmの正三角形をかきたいんだったら、
6cmの線分をかくだけさ。
線分の両端をA・Bとおこうか。
これが第一ステップさ!
つぎは、コンパスの出番。

コンパスで、
半々円を2つかいてやろう。
半半円とは、半円の半分のやつのこと。
つまり、
1つの円の4分の1サイズのやつさ。

そいつを、
さっきかいた線分の両端を中心にして、
かいてやればいいんだ。
1辺が6cmの正三角形のときも同じ。
まず、線分の端のAに針をおこう。
んで、
コンパスの鉛筆を逆のBにおく。
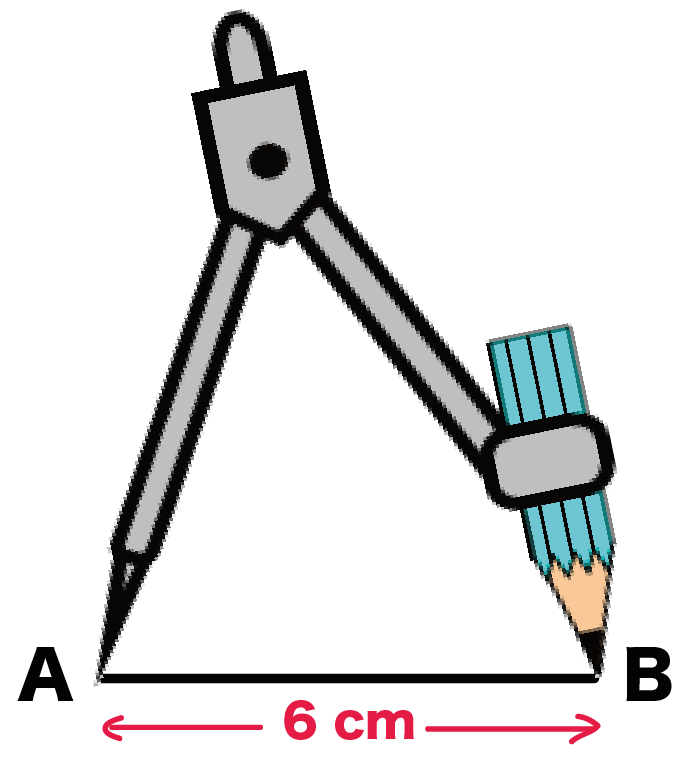
そして、
半半円をかく。
そのつぎは、逆のBにコンパスの針をおいて、
鉛筆をAにおく。
そして、
半々円をかく。
これで第二ステップは終了さ!
あとは、半半円の交点と線分の両端をむすぶだけ!
半々円たちの交点をCとしよう。
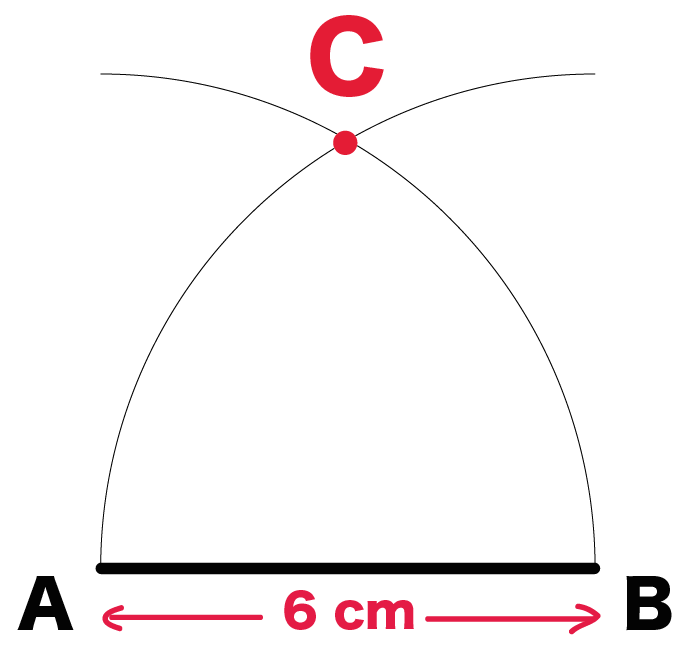
この交点Cと、
両端のA・Bを直線でむすべばいいんだ。
定規でむすんでみると、
あら!
正三角形ABCのできあがり!
正三角形をかきたい。
そんなときは、
コンパスと定規をさがそう。
そして、
使おう。
あとはゆっくり作図すれば大丈夫。
何度も練習してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。みかんは1日2個までだね。
正三角形の面積には公式がある。
便利でイカすヤツだ。
1辺の長さをaとすると面積は、
√3/4 a^2
になるんだ。
つまり、
(正三角形の1辺)×(正三角形の1辺)× √3 ÷ 4
ってことだ。
たとえば、1辺が6cmの正三角形ABCの面積を求めてみよう。

公式をつかって面積を計算すると、
(正三角形の1辺)×(正三角形の1辺)× √3 ÷ 4
= 6× 6× √3 ÷ 4
= 9√3 [cm^2]
になるんだ。
2秒で計算できちゃうね!
がしかし、だ。
公式をおぼえると便利だけど、
忘れた時に悲惨なことになる。
頭真っ白ってやつさ。
今日はそんなときのために、
正三角形の面積の求め方を3ステップで伝授しよう。
例として、
さっきの正三角形ABCの面積を求めていくよ。
頂角の二等分線を底辺にひいてみよう。
頂角が半分になる線をすーーーっと底辺にひけばいいのさ。
例の正三角形ABCでは、
AからBCにむかって二等分線をひけばいいんだ。
んで、
二等分線と底辺の交点をHとしよう。
二等辺三角形の性質の1つに、
頂角の二等分線は底辺を垂直に2等分する
ってものがあったね?
正三角形は二等辺三角形の1種だからこの性質がつかえる。
すると、
AH ⊥ BC
になるよ。
正三角形の高さを計算しよう。
つかうのは、
直角三角形の比
だ。
二等分線で半分にわかれた直角三角形に注目して。
例の△ABCでいうと、
△ACHね。
こいつは1つの内角(C)の大きさが60°の直角三角形だね。
だから、各辺の比は、
1: 2: √3
になっているはず。
よって、
高さAH = AC ×√3/2
= 6× √3/2
= 3√3
になるんだ。
メンドイときは正三角形の高さの公式をつかってもいいよ。
あとは面積の公式で計算するだけ。
公式って、
底辺×高さ÷2
だったよね??
三角形ABCでは、
になった。
公式で計算すると、
面積 = 底辺 × 高さ ÷ 2
= 6 × 3√3 ÷ 2
= 9√3 [cm^2]
になる。
おめでとう!
正三角形の面積をゲットできねー!
正三角形の面積の求め方には公式がある。
だけれども、
忘れたらテストで即死することになる.
公式の求め方をおぼえておくようにしよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ごぼうがうまいね。
正三角形の高さの求め方には公式があるよ。
それも、むちゃくちゃシンプル。
正三角形の1辺をa とすると、その高さは、
√3/2 a
で計算できちゃうんだ。

つまり、
(正三角形の1辺の長さ)× √3 ÷2
ってことだね。
たとえば、
1辺が6cmの正三角形ABCがあったとしよう。
公式で高さを計算すると、
6 × √3 ÷2
= 3√3 [cm]
になる。
ね?
簡単でしょ??
公式はむちゃ便利。
だけど、
忘れたら何もできなくなっちゃうよね?
だから今日は、
正三角形の高さの求め方を3つのステップで紹介していくよ。
公式をおぼえるのが苦手な人は参考にしてみてね。
例として、1辺6cmの正三角形ABCの高さを求めていこう!
頂角から底辺に二等分線をひいてみよう。
三角形ABCでいうと、
角Aが二等分される直線を、
BCにすーーーっとひけばいいんだ。
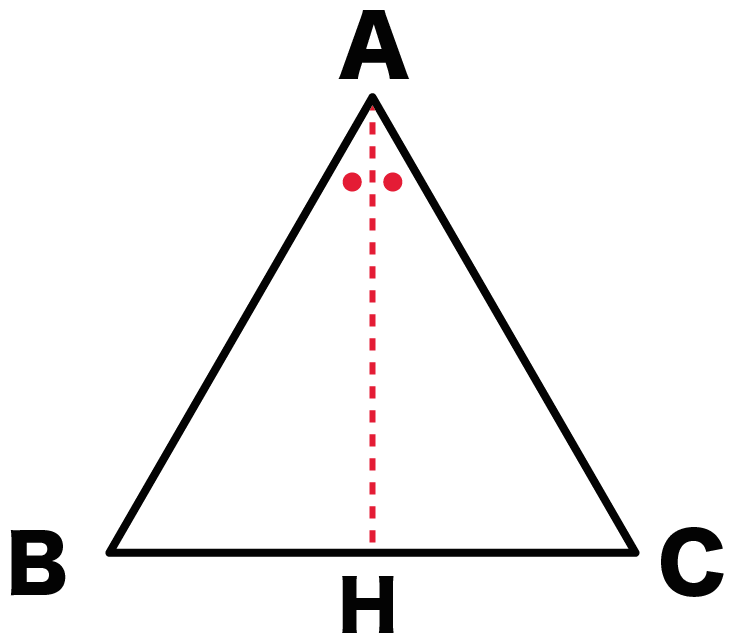
BCと二等分線の交点をHとおくよ。
これが第一ステップさ。
頂角の二等分線は底辺を垂直に2等分する
をつかってやろう。
正三角形は二等辺三角形の仲間。
だから、性質がつかえちゃうんだ。
これをつかえば、
AHはBCの垂直二等分線になっているはず。
よって、
AH ⊥ BC
になるね。
直角三角形の比で高さを計算しよう。
二等分線でできた、
小さい三角形に注目して。
△ABCでいうと、△ACHだね。
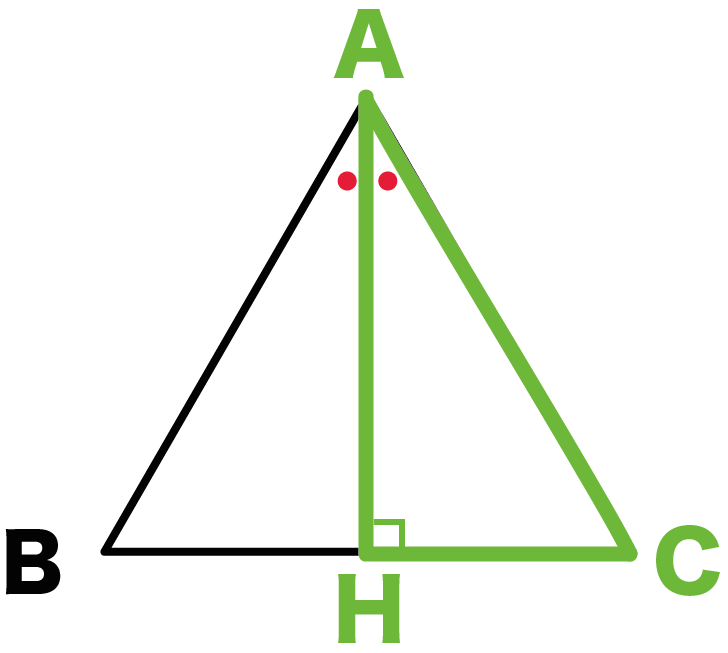
角Cは60°だよね??
だって、
正三角形の角度の大きさはぜーんぶ60°だからさ。
だから、
直角三角形ACHの各辺の比は、
1:2:√3
になっているはずだ。
AC = 6 cmだから、比をつかって高さAHを計算すると、
AH = 6 ×√3/2
= 3√3
になる。
これで正三角形の高さが計算できたね。
正三角形の高さはシンプル。
の3ステップでいいんだ。
じゃんじゃん攻略していこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。白米、最高。
正三角形の角度ってシンプル。
内角の1つの大きさは、
60°
なんだ。
しかも、ぜーーーんぶの内角が60°になっているよ。
先生に、
正三角形の角度はいくつ??
ってきかれたら、
60°ですがなにか??
っていえばいいよ。

今日はもう一歩ふみこんで、
正三角形の角度の求め方
を勉強してみよう。
なんで角度が60°になるんだろう・・・・
っておもったら読んでみてー
なぜ、正三角形の角度が60°になるのか??
をみていくよ。
例として、つぎの正三角形ABCをとりあげる。
3ステップで角度を求められるよー
1つの角度を文字でおこう。
正三角形ABCでは、
角B = a
としてみたよ。
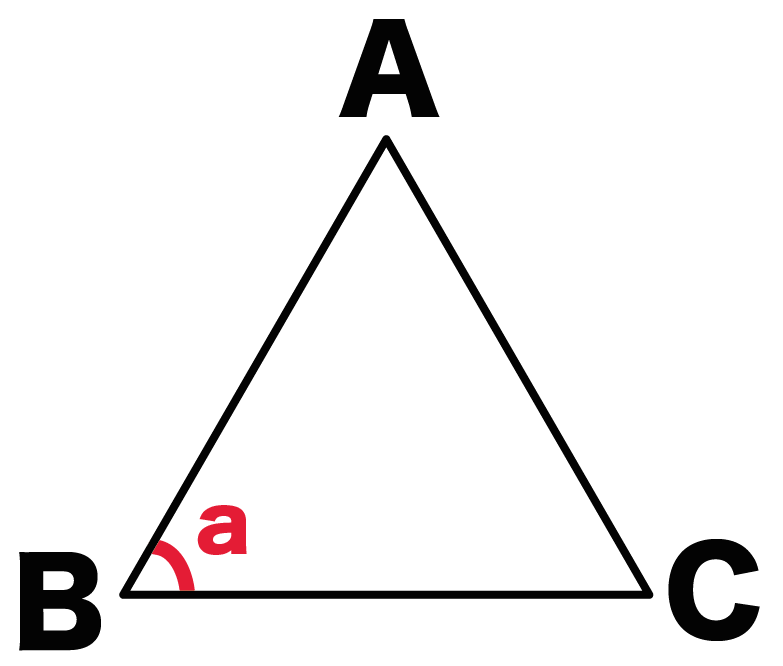
文字はなんでもいいよ。
bでもcでもxでもね。
つぎは二等辺三角形の性質である、
底角が等しい
という性質を使うよ。
正三角形の定義は、
3つの辺がすべて等しい三角形
だったよね?
ってことは、
2つの辺が等しい「二等辺三角形」でもあるわけだ。
例の正三角形ABCでいうと、
AB = ACの二等辺三角形ってことだね。
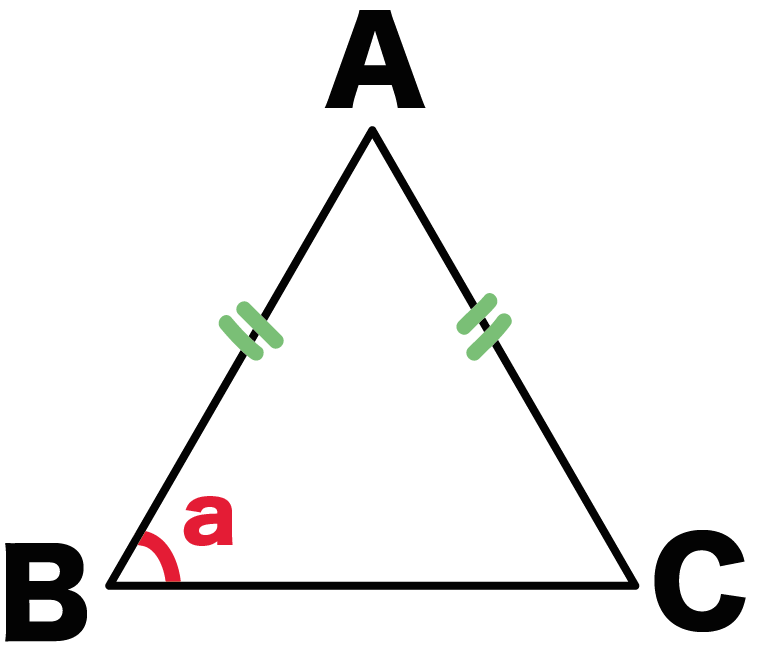
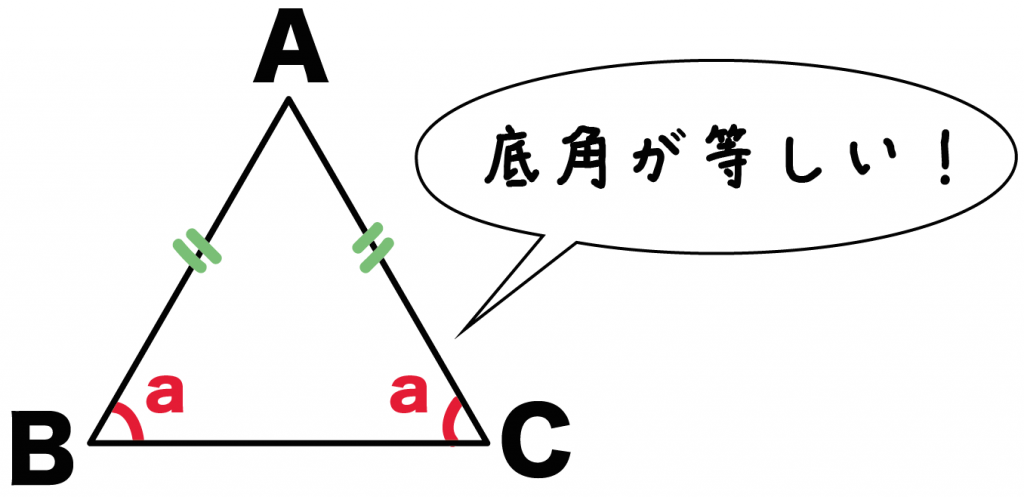
底角は等しい
という二等辺三角形の性質をつかってやれば、
角B = 角C = a・・・・(1)
であることがわかる。
おなじように、
正三角形ABCは、
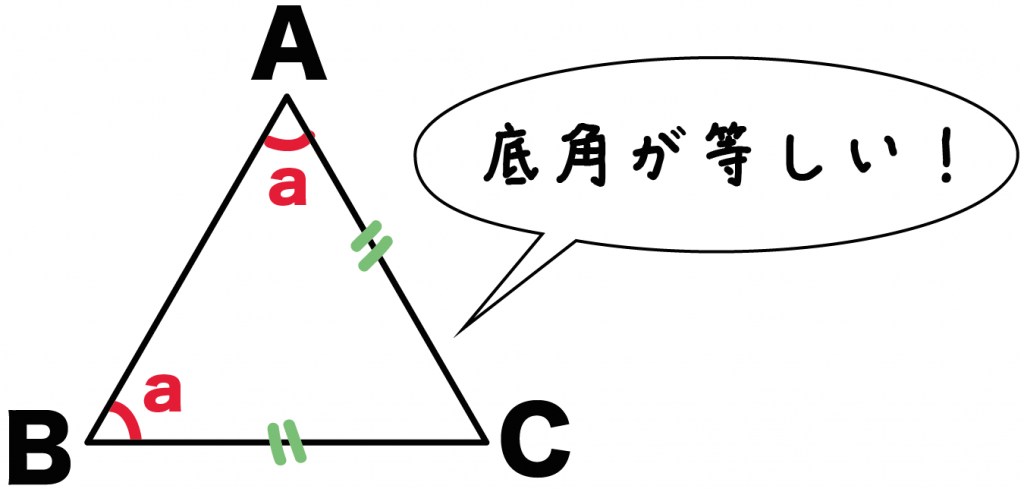
AC = BCの二等辺三角形でもあるわけだ。
だから、ここでも底角が等しいことを使ってやれば、
角A = 角B = a ・・・・(2)
ってことがいえるね。
(1)、(2)より、
角A = 角B = 角C = a
ってことがいえるんだ。
だから、
ぜーーんぶ角度が同じってことになるのさ。
正三角形の角度はぜーんぶ等しい。
ってことは、
1つの角度は、
内角の和を3でわったもの
ってことだ。
三角形の内角の和は180°なので、
180を3でわってやると、
180÷3
= 60°
になるね!
よって、正三角形の1つの角度は「60°」になるんだ。
角度の求め方で大事なのは、
正三角形を二等辺三角形としてあつかえるか?
だ。
底角が等しいことをつかって、
問題をといていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。チワワと遊びたいね。
数学を勉強していると、
正三角形(せいさんかくけい)
ってよくでてくるね??
名前はカッコイイけど、何者なんだろう・・・
って思うはず。
そこで今日は、
正三角形の定義をわかりやすく解説していくよ。
よかったら参考にしてみてね。
教科書によると、正三角形の定義とは、
3つの辺がすべて等しい三角形
ってかいてある。
つまり、
3つの辺がぜーーーーーんぶ等しい三角形だ!
たとえば、三角形ABCがあったとすると、
ぜーんぶの辺である、
がぜーーーーーんぶ等しいとき、そいつは正三角形なんだ。
つまり、
AB = BC = AC
のときだね。
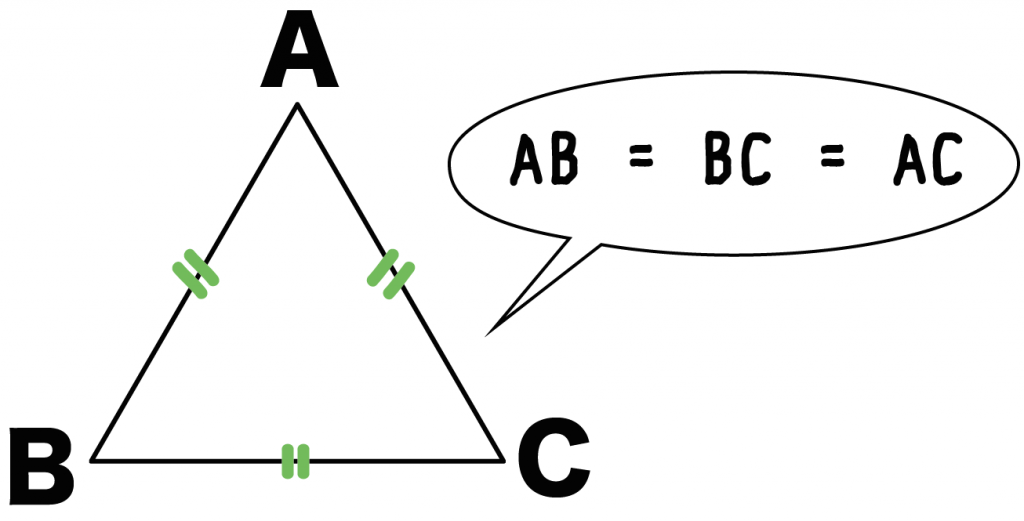
だから、
二辺が等しいだけだったら正三角形じゃないし、
ぜーーんぶ辺が等しくても
五角形だったら正三角形じゃないんだ。
あくまでも、
3つの辺がすべて等しい三角形
が正三角形ってことをおぼえておこう!
おぼえてほしいことが1つある。
それは、
正三角形は二等辺三角形の1種
ってこと。
つまり、
正三角形は二等辺三角形でもあるわけさ。
なぜなら、
3つの辺が等しい三角形ってことは、
2つの辺も等しいっていえるからね。
二等辺三角形の種類の中に、
正三角形っていう特別なヤツがいる
っていうイメージ。

だから、
正三角形ならば二等辺三角形である
っていえるけど、
二等辺三角形ならば正三角形である
とはいえないね。
たとえるなら、
「プードル犬」と「トイプードル」みたいな関係だね。
プードルが「 二等辺三角形」で、トイプードルが「 正三角形」にちかい。
トイプードルはプードルっていう犬の種類のなかの1つだよね??
ただ、プードルっていう犬にはトイプードル以外もいる。
スタンダード・プードルとか、
ミディアム・プードルとかね。
だから、
トイプードルをプードルってよんでも問題ないけど、
プードルをトイプードルをよんでは間違いだ。
これは、
二等辺三角形は正三角形ではないけど、
正三角形は二等辺三角形である関係といっしょだね!
正三角形の定義はシンプル。
ぜーんぶの辺が等しい三角形のことをいうのさ。
テスト前によーく復習しておいてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。メンマラーメンはまるね。
直角二等辺三角形の面積を求めたい、
ってときあるよね。
宿題にでるときあるし、
テストにひょっこりでることもある。
ぜひ、面積の求め方をおぼえておきたい。
そこで今日は、
直角二等辺三角形の面積の求め方の公式
を2つのパターンにわけて解説していくよ。
よかったら参考にしてみて。
公式には2パターンある。
問題によってつかいわけよう!
まず、斜辺以外の長さがわかる場合だ。
公式はチョー簡単。
三角形の面積公式の、
底辺×高さ÷2
をつかってやればいいんだ。
斜辺以外の長さをaとすると、
面積 = 1/2 a^2
になるよ!
たとえば、
斜辺以外が6cmの直角三角形ABCがあったとしよう。
こいつの面積は公式は、底辺×高さ÷2だから、
6×6÷2
= 18 [cm^2]
になるね。
ばんばん計算しようぜ!
直角二等辺三角形の「斜辺しか」わかっていない問題だ。
斜辺の長さをbとすれば、
面積 = 1/4 b^2
っていう公式で計算できるよ。
つまり、
斜辺×斜辺÷4
で計算できちゃうんだ。
たとえば、斜辺が4 cmの三角形DEFがいたとしよう。
この直角二等辺三角形の面積は、
4 × 4 ÷ 4
= 4[cm^2]
になるはず!
チョー簡単な計算だね。
えっ。
なんでこの公式がつかえるのかって??
せっかくだから説明しよう。
斜辺がbの直角二等辺三角形ABCがいたとする。
頂角Aから二等分線を底辺BCにひく。
交点をHとしよう。
二等辺三角形の性質をつかうと、
AHは底辺BCの垂直二等分線になるはずだ。
つまり、
だね。
また、
角C = 角CAH = 45°
よって、
△ACHも直角二等辺三角形になる。
だから、
AH = CH = 1/2 b
だ。
AHは△ACHの高さ。
△ACHの面積を計算してやると、
1/2 b × 1/2b ÷2
= 1/4b^2
になるんだ。
ちょっと複雑だけど、
計算式は簡単!
じゃんじゃん使っていこう。
直角二等辺三角形の面積は公式はカンタン。
の2パターンで面積を求めよう!
公式は便利だけど、
なぜ公式がつかえるのか??
ということもしっかりおさえてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。そぼろごはんはうまいじゃん。
直角二等辺三角形の辺の長さ
を計算したいときあるよね?
たとえば、
直角二等辺三角形の面積を求めるときとか、
家具の寸法をはかりたいときとかね。
今日は、
直角二等辺三角形の辺の長さがわかる公式
をわかりやすく解説していくよ。
よかったら参考にしてみてー
求め方には2パターンある。
順番にみていこう!
まず、
斜辺以外の長さがわかってるときの場合だね。
つぎの公式で計算できちゃうんだ。
辺の長さをa、斜辺をbとすると、
斜辺b = √2 a
になる。
たとえば、
斜辺以外が6cm の直角二等辺三角形ABCがあったとしよう。
このとき、
斜辺の長さABは、
AB = 6 × √2
= 6√2
になるね。
√2をかけるだけだから簡単だね。
つぎは、
直角二等辺三角形の「斜辺だけ」わかってる場合だ。
このとき、
残りの辺はつぎの公式で計算できるよ。
斜辺をb、等しい辺の長さをaとすると、
a = √2b /2
で求められるんだ。
たとえば、
斜辺が4cmの直角二等辺三角形DEFがいたとしよう。
こいつの斜辺以外の長さは公式をつかうと、
EF = √2/2 × 4
= 2√2 [cm]
になるよ!
分数の計算だからミスをしないように気をつけてね。
直角二等辺三角形の辺の公式はシンプル。
で計算できちゃうんだ。
ガンガン問題をといていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。馬、うまいね。
二等辺三角形って、
2つの辺が等しい三角形のこと
だったよね??

名前はかっこいいし、
ルックルも、いい。
人気がありそうな三角形だ。
だけれども、
二等辺三角形にはどんな性質があるんだろう??
って疑問に思うよね。
そこで今日は「二等辺三角形の性質・定理」をわかりやすく説明していくよ。
よかったら参考にしてみて。
二等辺三角形には2つの性質があるんだ。
ってやつだ。
順番にみていこう!
ひとつ目の性質は、
底角が等しい
ってやつさ。

底角とは、
底辺をはさんでいる角のこと
だったね?
なんと、
二等辺三角形では底角の大きさが等しいんだ。
たとえば、つぎの二等辺三角形ABCがあったとしよう。
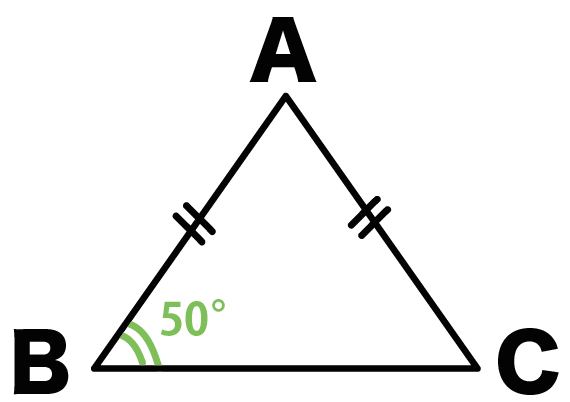
っていうスペックをもっているヤツさ。
このとき、
二等辺三角形の底角は等しいから、
角B = 角C = 50°になるんだ。
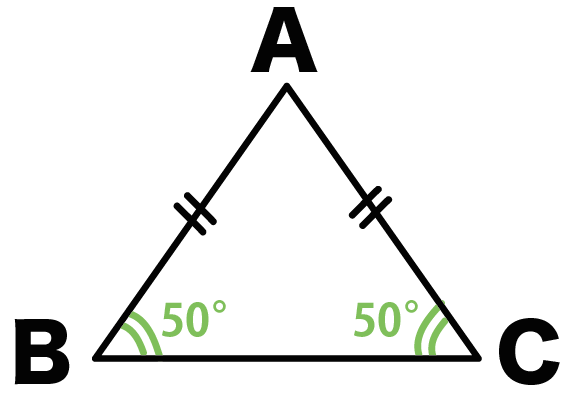
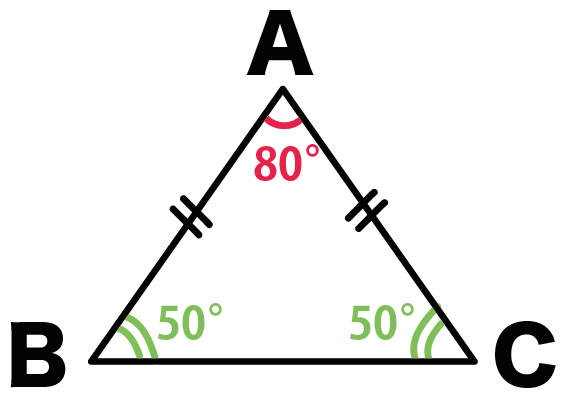
頂角はどうなるかっていうと、
内角の和180°から2つの底角をひいて、
180°- (50+50)
= 80°
で計算できるよ。
2つの目の性質は、
「頂角の2等分線」が「底辺の垂直2等分線」になる
ってやつだ。
びみょうにすごいよね?。
たとえば、つぎの三角形DEFがいたとしよう。
っていうスペックをもっている。
このとき、
頂角Dの二等分線を底辺EFにむけてひいて、
底辺との交点をGとする。
すると、
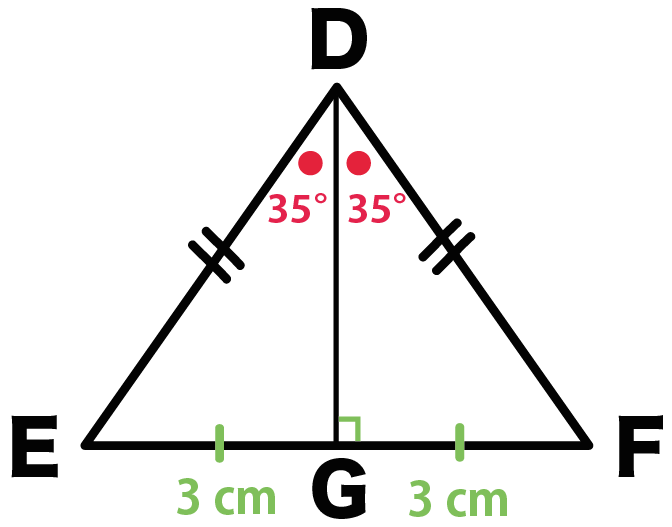
になるよ。
つまり、
DGは底辺EFの垂直二等分線になっていると
いうことなんだ。
二等辺三角形の性質の、
ってことを解説してきたよ。
この性質は定理として、
証明や計算問題で自由につかうことができる
んだ。
じゃんじゃんつかって問題を攻略していこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。本屋で豪遊したね。
世界にはたくさん三角形が、いる。
その数、
おおよそ、
うーん、たぶん数えきれないね。
そんな中、ある特殊な三角形がいる。
そいつの名は、
二等辺三角形
というものさ。

今日は、
二等辺三角形とはなにものか??
ってことを振り返っていこう!
定義がわからんときに参考にしてみて。
教科書によると、二等辺三角形の定義は、
2つの辺が等しい三角形
ってかいてあるね。
3つの辺がばらばらの三角形は、
二等辺三角形でもなんでもない。

2辺が等しい「五角形」も二等辺三角形でもないね。
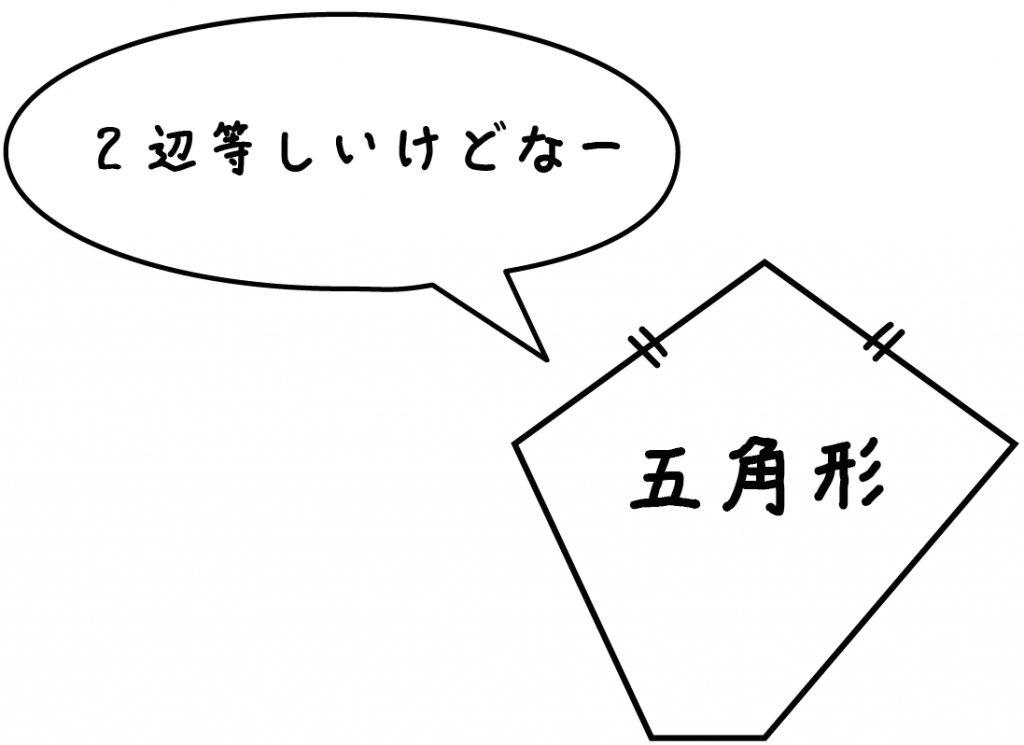
2つの辺が等しい三角形だけを
二等辺三角形
というんだ。
二つの等しい辺をもった三角形
でおぼえてみよう。
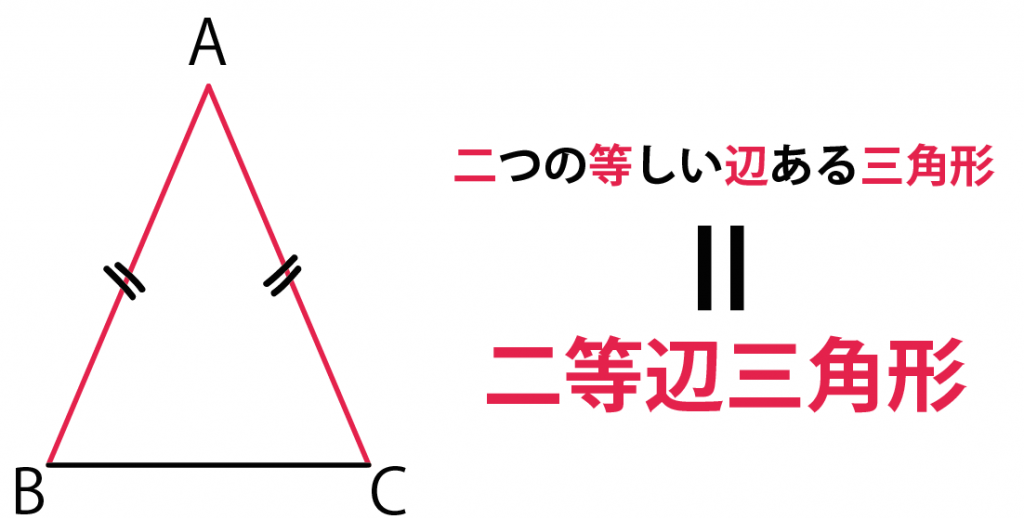
つぎは、
2等辺三角形のパーツをおぼえていこう。
順番にみていくよ。
等しい2辺にはさまれた角を、
頂角(ちょうかく)
ってよんでいるよ。

えっ。
名前をおぼえられないだって?!?
そんなときは、
2つの等しい辺にはさまれて有頂天になっている角
っておぼえてみて。
頂角の向かいの辺を
「底辺(ていへん)」
っていうんだ。
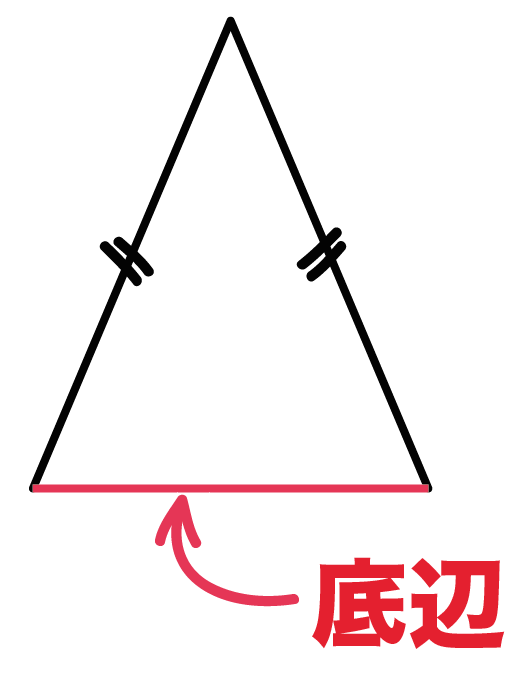
頂角と向き合っててーへんだ(大変だ)
っておぼえてみよう。
最後に、底辺をはさんでいる両端の角を
底角(ていかく)
っていうよ。
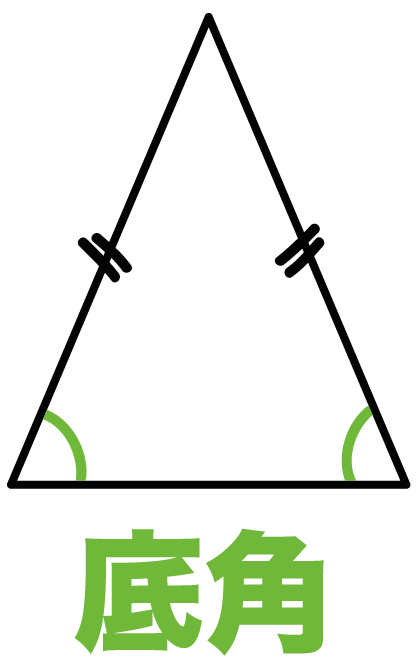
これは覚え方むずいね。
うーん、
ふつうに、ベーシックにおぼえると、
底辺をはさんでいる角
がいちばんしっくりくるかもね。
こんな感じで、
二等辺三角形のパーツにはたくさん名前がついてるよ。
がんばっておぼえてみてね。
二等辺三角形はあんがいシンプル。
2つの辺が等しい三角形
だったよね。
ひまがあったらパーツの名前もおぼえていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鼻呼吸したいね。
二等辺三角形の角度を求める問題
ってあるよね??
慣れれば簡単にとけるけど、
はじめはすごく大変なはず。

そこで今日は、
二等辺三角形の角度の求め方の公式
を2パターン紹介するよ。
テスト前に参考にしてみて。
二等辺三角形の角度は2パターンで計算できちゃうよ。
順番に紹介していくよー!!
まずは、
2等辺三角形の「頂角」がわかっている問題だ。
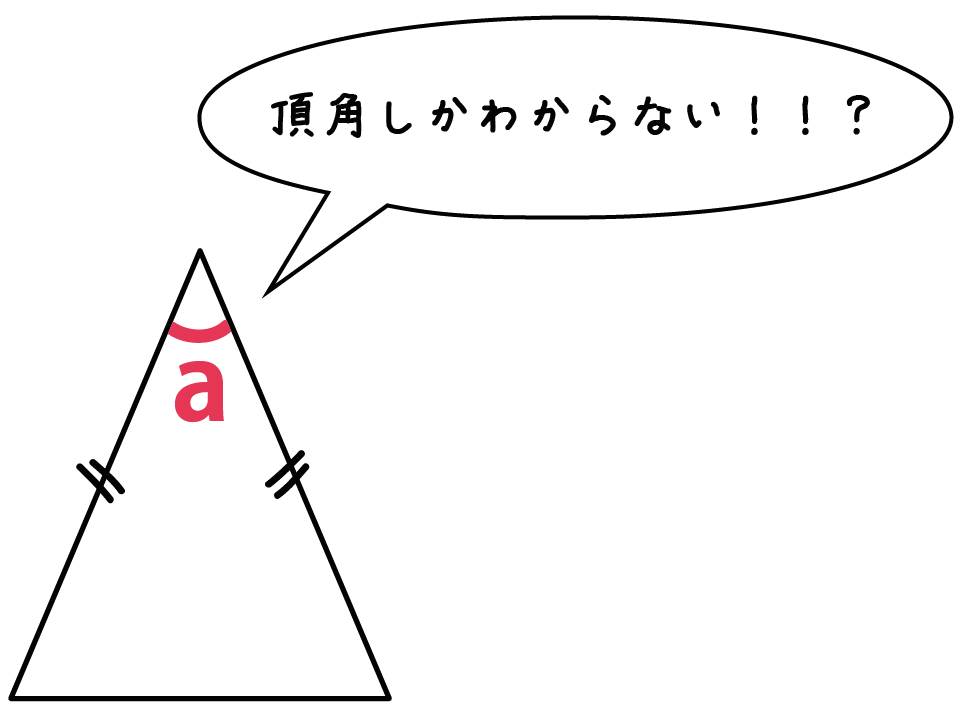
この問題では、
つぎの公式がつかえるよ。
頂角をa°とすると、
底角b = (180-a)/2
になるんだ。
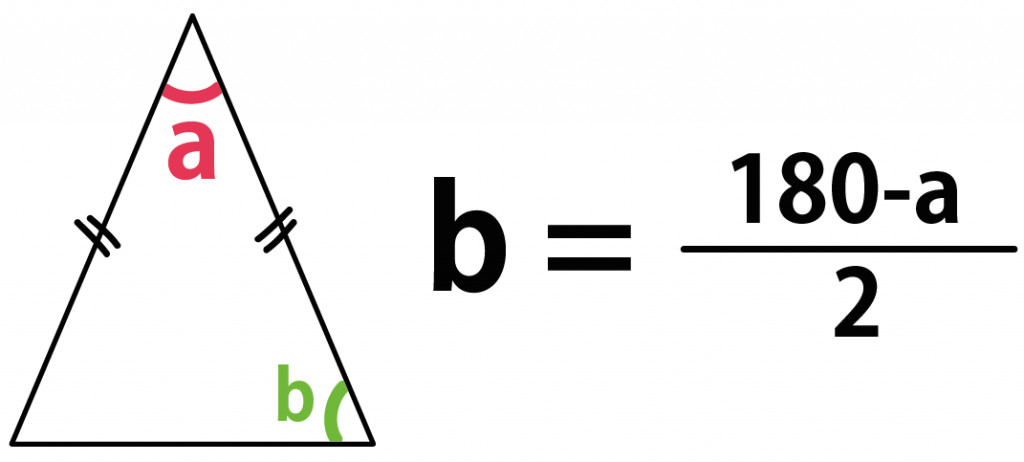
公式の計算もシンプル。
どんどんつかってみよう!
たとえば、つぎのような問題があったとしよう。
例題1
AB = AC の二等辺三角形で、角A=40°のとき、aの値を求めなさい。
頂角は40°だから、
さっきの公式のaに「40°」を代入してみよう。
すると、
底角b = (180-a)/2
= 140/2
= 70°
になるね。
でも、なぜ公式がつかえるんだろう??
二等辺三角形の底角は等しいから、
角B = 角C
になるね。
ってことは、
内角の和(180°)から頂角(40°)をひいて、2でわったやつが、
底角Bの大きさってことになるんだ。
よって、
b = (180-40)/2
= 70°
になる。
2つめは底角しかわかっていないパターンだ。
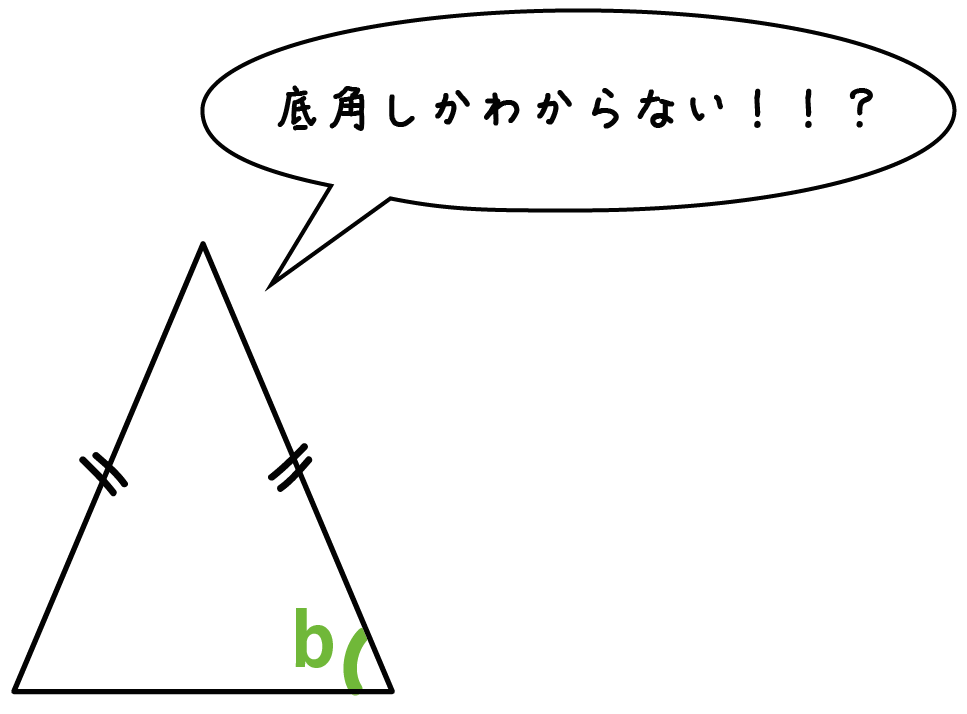
つぎの公式をつかってみて。
底角をbとすると、
頂角a = 180-2b
になるんだ。
つぎの例題で公式をつかってみよう!!
例題2
AB = AC の二等辺三角形で、角B=65°のとき、aの値を求めなさい。
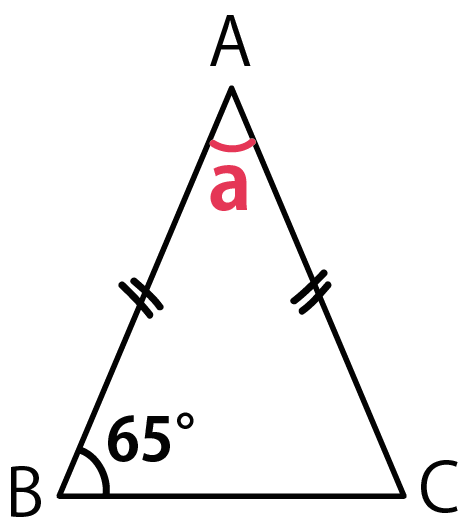
公式に底角65°を代入してやると、
頂角a = 180 -2 × 65
= 50°
になるね。
なぜ公式がつかえるんだろう??
底角は等しいから、
角B = 角C = 65°
になる。
ってことは、残りの頂角Aは、
三角形の内角の和(180°)- (角B+角C)
で計算すると、
180- (65+65)
= 50°
になるね!
2等辺三角形の角度の問題は、
の2パターンだね。
この基礎さえつかんでおけ大丈夫。
応用問題もとけるようになるよ。!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。図書館、最高。
数学の証明はむずいよね??
雰囲気がめんどいのはもちろんだけど、
それ以上に、
証明の書き方がわからない!
からだと思うんだ。
だって、
先生ごとに書き方ちがうからね。
誰を信じたらいいのかわからなくなっちゃう。

そこで今日は、
【中学数学】3年間つかえる証明問題の書き方
って記事をかいてみたよ。
困ったときに参考にしてみて。
証明の書き方でおぼえてほしいのは、
型だよ。
ちまたではテンプレートともよばれてる。
そうだなあ、
クッキーを思い浮かべてほしい。
だいたい同じような形のクッキーが焼けるのって、
型があるからなんだ。
だから、
数学の証明でも「型」を使いこなせれば、
それっぽい証明が何個でもつくれることになるね。
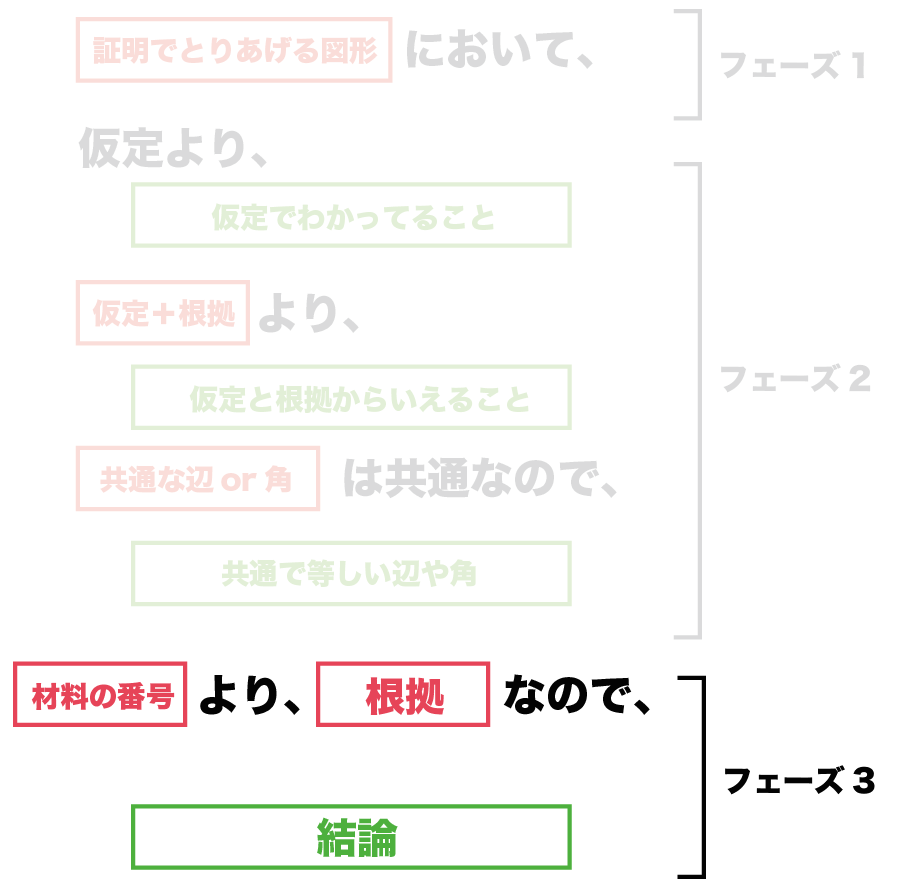
書き方の「型」はつぎのものだよ。
先生ごとによって書き方ちがうけど、
ぶっちゃけどれもこんな感じだ↓↓
(証明でとりあげる図形)において
仮定より、
(仮定よりわかっていること)
仮定+根拠より、
(仮定と根拠からいえること)
(共通な辺or 角)は共通なので、
(共通で等しい辺や角)
(材料の番号)より、(根拠)なので、
結論
じつはこの型、
っていう、3つのフェーズにわかれている。
この「型」で例題をといてみよう!
例題
AB = DC、AB // DCの△ABCと△CDAがあったとします。
このとき、△ABC≡△CDA
を証明しなさい。
書き方のいちばん最初は、
どの図形を証明でとりあげるのか??
を宣言することなんだ。
〜において
ってかいて、
「〜」には「証明でとりあげる図形」をかいてあげよう。
例題では、
△ABCと△CDAの合同を証明していくよ。
ってことは、この証明ではおもに、
△ABCと△CDA
の話をしていくことになるんだ。
だから、証明のいちばん最初で、
△ABCと△CDAにおいて、
って証明でとりあげる図形を宣言してみて!
このフェーズはぶっちゃけ、
あってもなくても構わない。
だけどこいつをかいてやることで、
っていうメリットがあるんだ。
ぜひ、証明のいっちゃん最初に
「証明でとりあつかう図形」を宣言してみてくれ!
結論に必要な材料をならべるフェーズだ。
をどんどんかいていこう!
結論の材料の並べ方はつぎの3パターンがあるよ。
このパターンをぜんぶ使わなくてもOK。
1つでも2つでも、ぜーんぶつかってもいいよ。
その証明に必要なものをチョイスしてみてね。
例題ではこんな感じになる↓↓
それぞれに番号ふるのを忘れずに!
最後はいよいよ結論。
フェーズ2で生み出した材料から、
結論(証明のゴール)
をみちびいてやろう。
書き方としては、
(材料の番号)より、(根拠のあることがら)なので、
(結論)である。
がのぞましいね。
例題でいうと、こうなる↓↓
もし、結論が「角ABC = 角CDA」だった場合は、
もう一回フェーズ3をくり返してみてね。
こんな感じで、問題によって、
フェーズ2や3が数回くり返すこと
もあるよ!
必ずしもこの型がピタリとはまるわけじゃないから、
気をつけてね。
数学の証明はぶっちゃけむずい。
解き方もようわからん。
だけど、
書き方の「型」をおぼえてしまえば大丈夫。
それ通りにかいていくだけでいいからね!
問題をときまくって書き方になれていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鍋つくりたいね。
正多角形の外角の大きさがわからない・・・・・
そんなときは公式をつかえば一発。
正n角形の外角の1つの大きさは、
360°/n
になるんだ。
たとえば、正五角形の外角を求めてみよう。
公式のnに「5」を代入してやればいいから、
360°/ n
= 360°/ 5
= 72°
になるね。
つまり、正五角形の外角の1つの大きさが「72°」になっているってことさ。
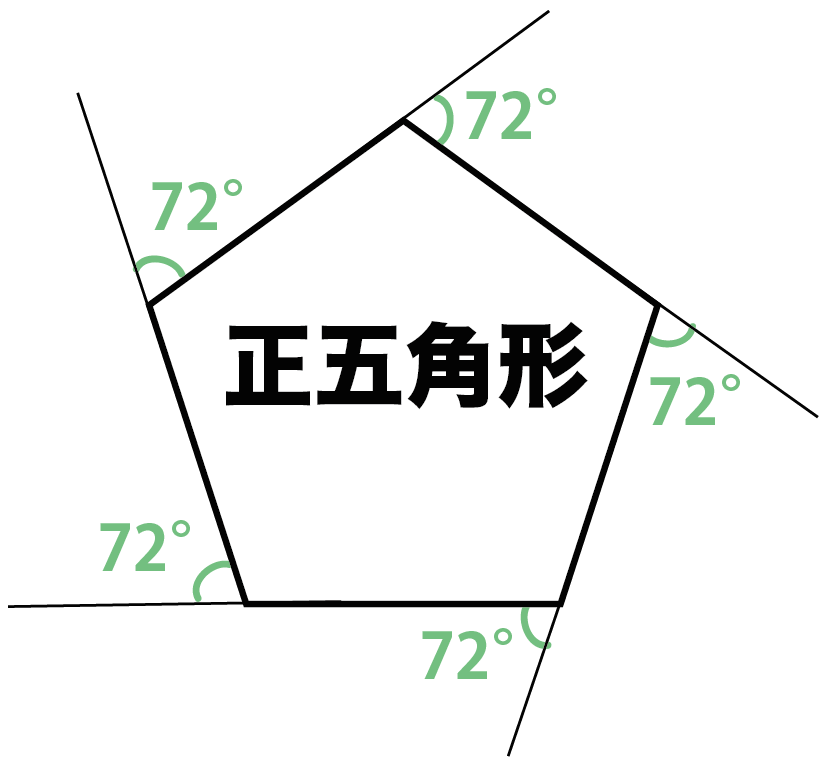
どう??神秘的でしょ??。
nに頂点の数をいれるだけでいい。
むちゃくちゃ便利だよね?
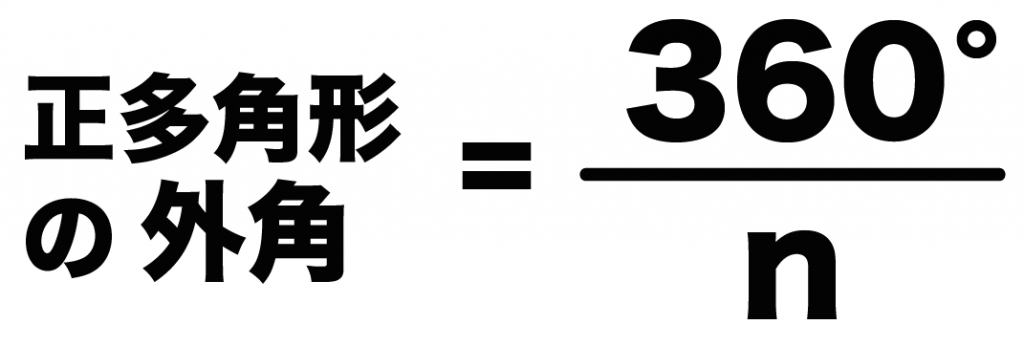
せっかくだから、
なぜ、
360°/n
で正計算できるか振り返ってみよう。
正多角形だろうが、何角形だろうが、
多角形の外角の和は360°になるって勉強したよね??
んで、
正多角形には「すべての内角が等しい」という性質がある。
ってことは、
内角と隣り合っている「外角もすべて等しい」ってことになるよ。
だから、正多角形の1つの外角の大きさは、
(多角形の外角の和)÷ n
= 360°/n
になるんだ。
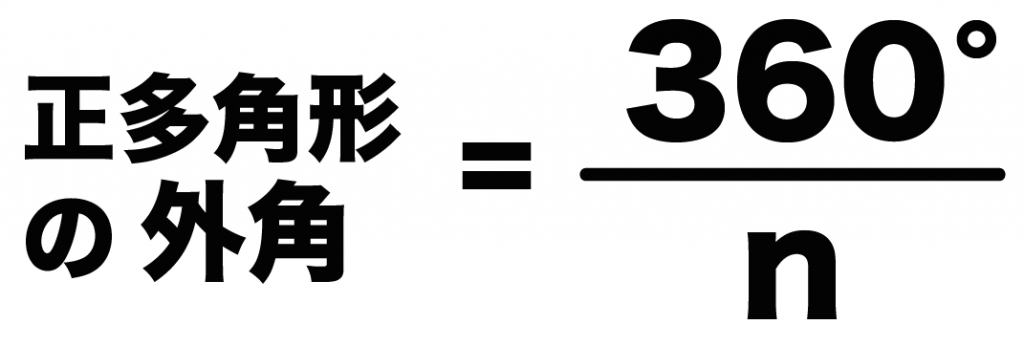
ただ公式をつかうだけじゃなくて、
なぜ、使えるのか??
ってこともおさえておこう!
正多角形(n角形)の大きさは、
360°/n
で計算できちゃうよ。
テストで出たらガンガン得点をうばっていこう!
そんじゃねー
Ken