こんにちはー!さしみこんにゃくが好きなKenだよー 今日も一緒に中学数学の勉強をしていこう!!
方程式の文章題で「速さ」のやつを苦手って子が多いよね??
たしかに時速とか分速とか速さとかよくわからないし、図を描いても解けそうな気がまったくしてこない。これは弱ったね。

あまり知られてないけれど、
速さの文章題をすばやく解くには、
速さ・時間・道のり(距離)
という3つを理解していることが必須になってくるんだ。だから、今日はこの「速さ」・「時間」・「道のり(距離)」を順番にゆっくりと説明していくね。
これらの3つを踏まえて「速さの公式」もおぼえてみよう。
記事を読み終わる頃にはきっと、文章題の速さ問題が得意になっているはずだよ!!
~もくじ~
「道のり」とか「速さ」とか「時間」はどんなときに必要なんだろう?? ふだん見かけないからちょっと気になるよね??
じつは、
「人やもの」が「地点A」から「地点Bまで」移動したときに必要なんだ。
たとえば、小学1年生の太郎くんが「自宅」から「図書館」へ自転車で移動した、
みたいにね。
この「移動のイベント」が発生したとき、「道のり(距離)」や「速さ」が必要になってくるんだ。
最初に理解したいのは「道のり」の意味だね。
ずばり、
道のりとは、
ある人や物が移動した距離
のことなんだ。たとえば、さっきの例で、太郎くんが家から図書館まで移動したよね?? このときの「道のり」は「家から図書館までの距離」ってことなんだ。
調べてみると、家から図書館までの距離はちょうど2kmだっとしよう。
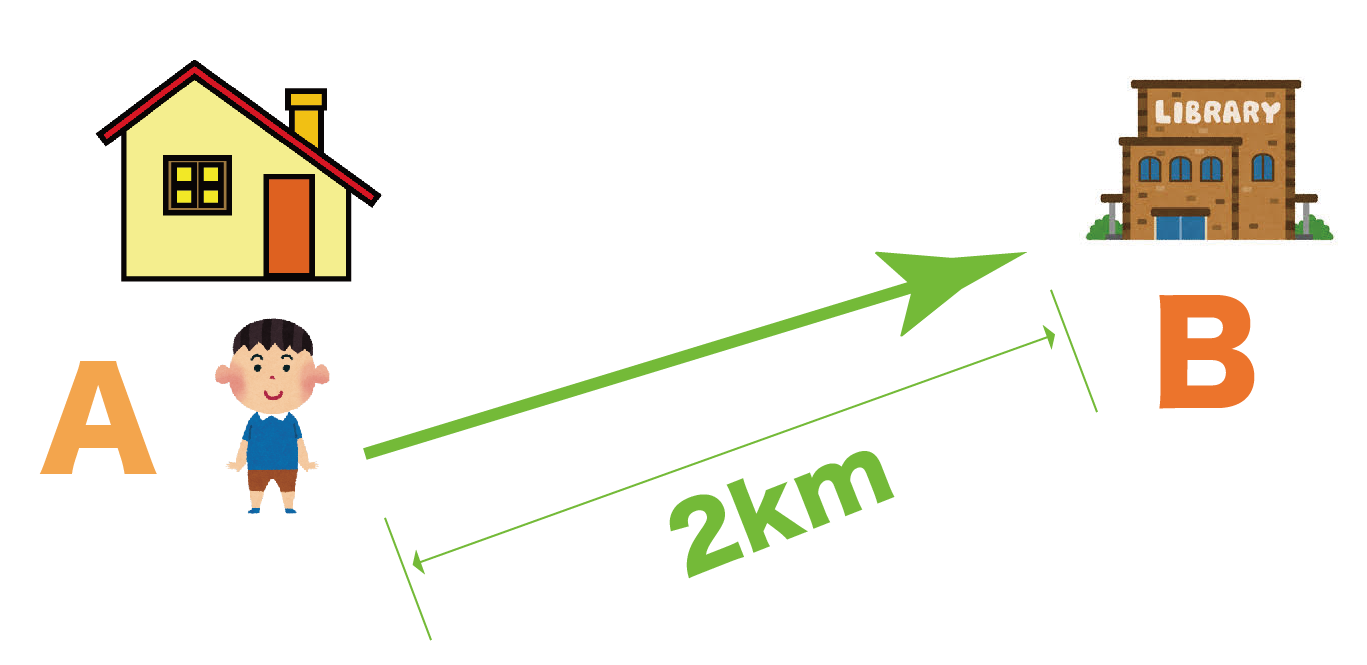
このとき、太郎君が移動した「道のり」は、
2km
ってことになるんだ。道のりも意外とカンタンでしょ??
次に「時間」ってなにかってことを見ていこう。
時間とはずばり、
ある人やものが移動した時間
のことだよ。たとえば、太郎君が2kmさきの図書館まで10分かかって自転車で移動したとしよう。
このとき、時間は「10分」ってことになる。だって、太郎くんの移動に10分かかってるからね。
これで時間と道のりはオッケーだね!!。
最後に「速さ」ってなにかってことを見ていこう。速さとは、
一定時間あたり進む距離
のことなんだ。ちょっとよくわからないね?? さっきの太郎君の例をみてみよう。
太郎くんは、
2kmを10分かけて移動した
よね??
これは間違いない。じゃあ、太郎くんは1分間あたりに何km進んだことになるかな??
そう、0.2kmだ。

2kmを10で割ると出てくる答えだね。なぜ10で割るのかっていうと、1分間あたりに進む距離を出したいからだ。
0.2kmを10倍すれば2kmになるよね?? つまり一分間に0.2kmすすむことができる速さで10分移動したってことを意味するんだ。
この場合は、一定時間を「1分間」としているね。このときの速さのことを「分速」っていうんだ。ぼんやりと覚えておこう!
これらを踏まえた上で「速さの公式」ってものが誕生する。
それは次の3つだ。
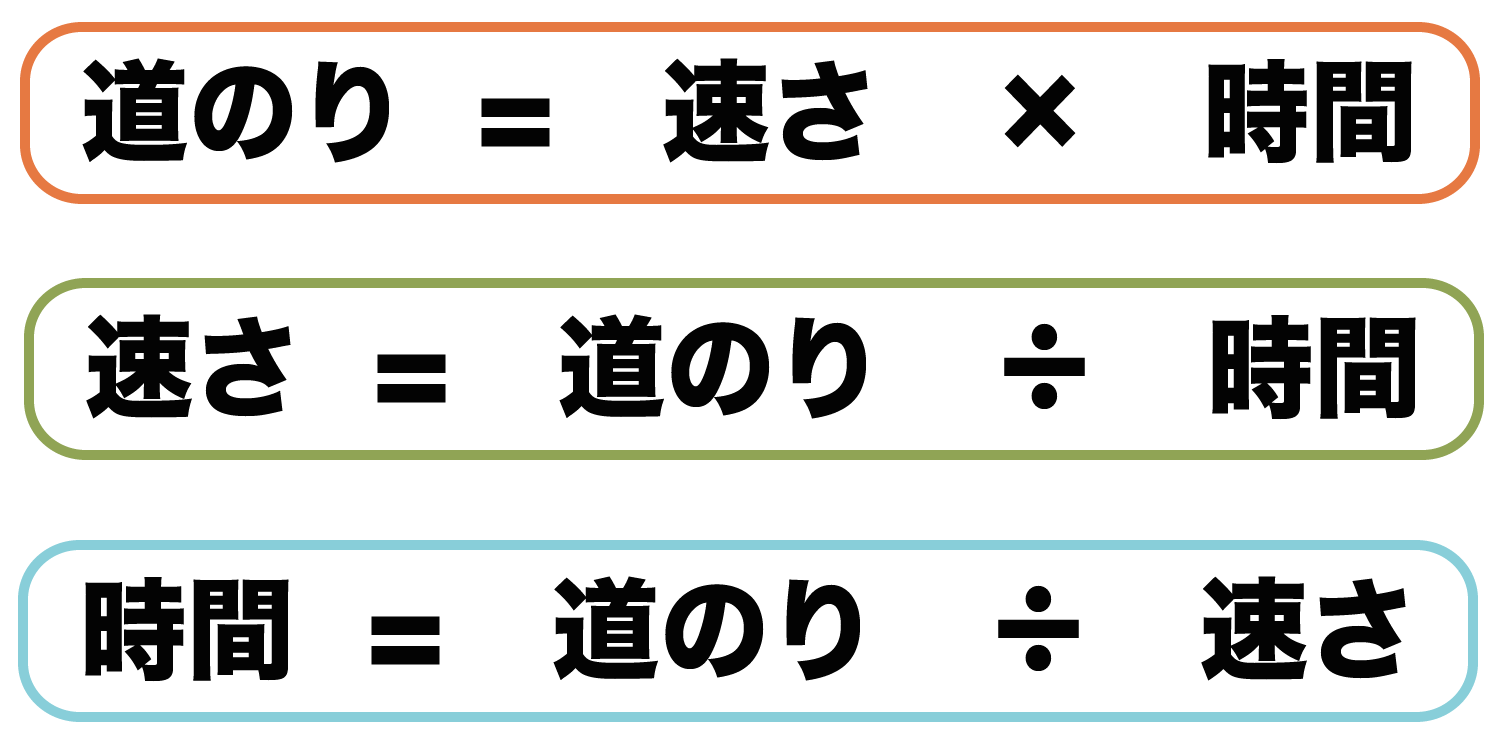
ちょっと公式が3つもあったら覚えにくいよね?? そんなときに使いたいのが次のアイテムだ。
名付けて、
速さ公式はやみ図
だ。
ちょっとドラゴンボールみたいに見えるけど、実際はもっとすごいものかもしれない。
使い方はいたってカンタン。
求めたいものを指で隠すだけ。
たとえば、「道のり」を求める公式を知りたいときは、こうやって親指をつかって道のりの欄を隠してあげるんだ。
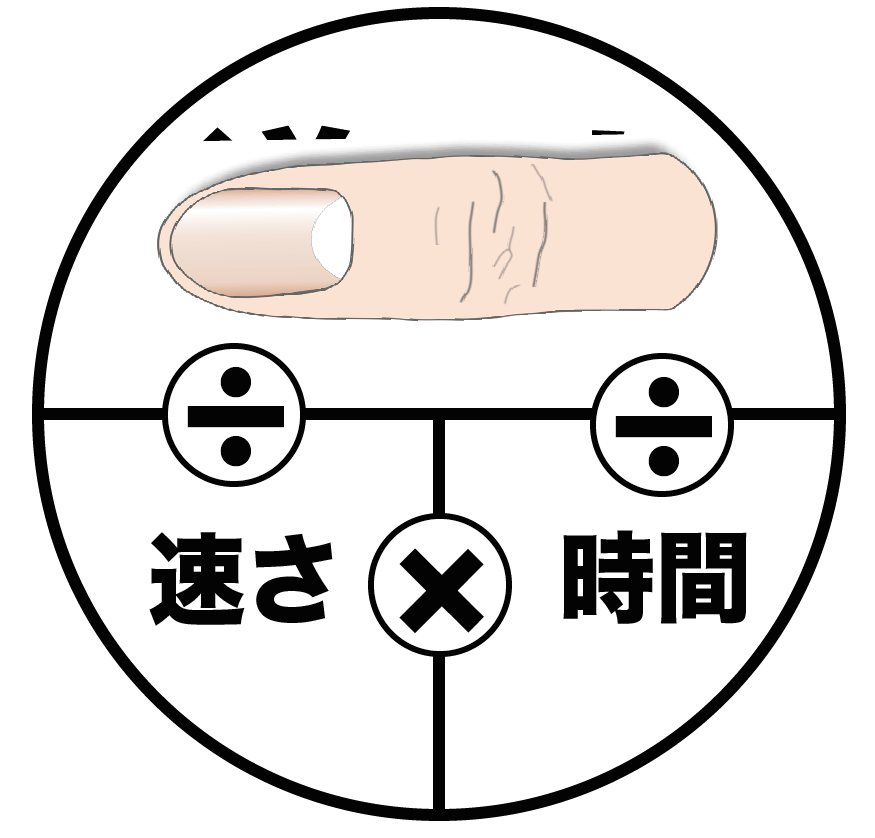
すると、「速さ×時間」っていう公式がでてくるでしょ?? これで「道のり」が求められるわけだ。
「速さ」も「時間」も同じように求めることができる。
「速さ」を求めたければ、「速さ」を指で隠したら「道のり÷時間」っていう公式が出現するし、
「時間」を隠せば、「道のり÷速さ」の公式がゲットできるんだ。
ね?? 便利でしょ! 速さの公式を忘れそうな時はつかってみてね。
次回は速さの単位について説明していくねー!!
それじゃねー!
Ken
こんにちは、リアルゴールドでシャキっとしたKenだよー!
方程式の文章題でいちばんむずかしいのは「速さ」に関するものだね! 文章題が苦手だと余計にヤッカイにみえちゃうんだ。
だけど、基本を押さえればどんな速さの文章題でも解けるようになるよ。
だから今日は、速さの文章題の方程式が苦手というキミのためにこんな記事を書いたんだ。
【苦手克服】方程式で速さの文章題を攻略する4つのコツ
ってやつさ。速さの文章題に苦手意識を持っていたら参考にしてみてね。
ソレ以前に一次方程式の文章題ぜんたいに苦手意識を持っているときは「【方程式の利用】一次方程式の文章題の4つの解き方」っていう記事がおすすめだよ。
速さの文章題を攻略するために知っておきたいコツは次の4つだ。よーく目をこらして確認してくれ!
速さに関する文章題をすらーっと解くためには基礎知識を身につける必要があるんだ。速さの文章題での基礎知識って、
の3つの用語の意味を理解すること。これに尽きる。
意味と使い方さえ覚えてしまえば、速さの文章題もイチコロさ!
速さ・道のり・時間
の3つに関しては別の記事で徹底的に解説したのでそっちをみてみてね!ゆっくり読めばきっとわかるはず。
速さの文章問題で間違えやすいのは単位の違い。
これを知らないで文章題と取っ組み合うと返り討ちにあっちゃうね。
それぐらいけっこうヤッカイな問題なんだ。
たとえば、「みちのり」には、
km・m・cm
といった単位があるし、
「速さ」には、
時速○○km、分速○○m、秒速○○mといった単位があるね。もちろん、時間にも、
時間・分・秒
といった単位がある。このたくさんある単位たちの関係を知っておけば大丈夫! 速さの文章題なんかビビることないんだ。
「速度の単位変換の記事」は別に書いたからこっちを参考にしてみてね!!
方程式の文章題の第一ステップは、
なにをxとおくか??
だったよね。速さの文章題はただでさえむずかしいから、なにをxとおくか迷っちゃうはず。だけれど、超難関校の入試問題じゃない限り、
文章題の中で
求めてね。
っていわれているものをxとおけばいいんだ。あ、でも単位には気をつけてね。
たとえば、
文章題の最後に、
家から図書館までの道のりは、何kmですか??
って書いてあったら、「家から図書館までの道のり」を「x km」とすればいいんだ。文章題の最後をみるだけだからカンタンでだね!
速さの文章題でも図をかくとわかりやすいんだ。
自分の好きなようにどんなグラフをかいてもいいけど、ぼくが気に入っているのはこんな感じの図 ↓↓
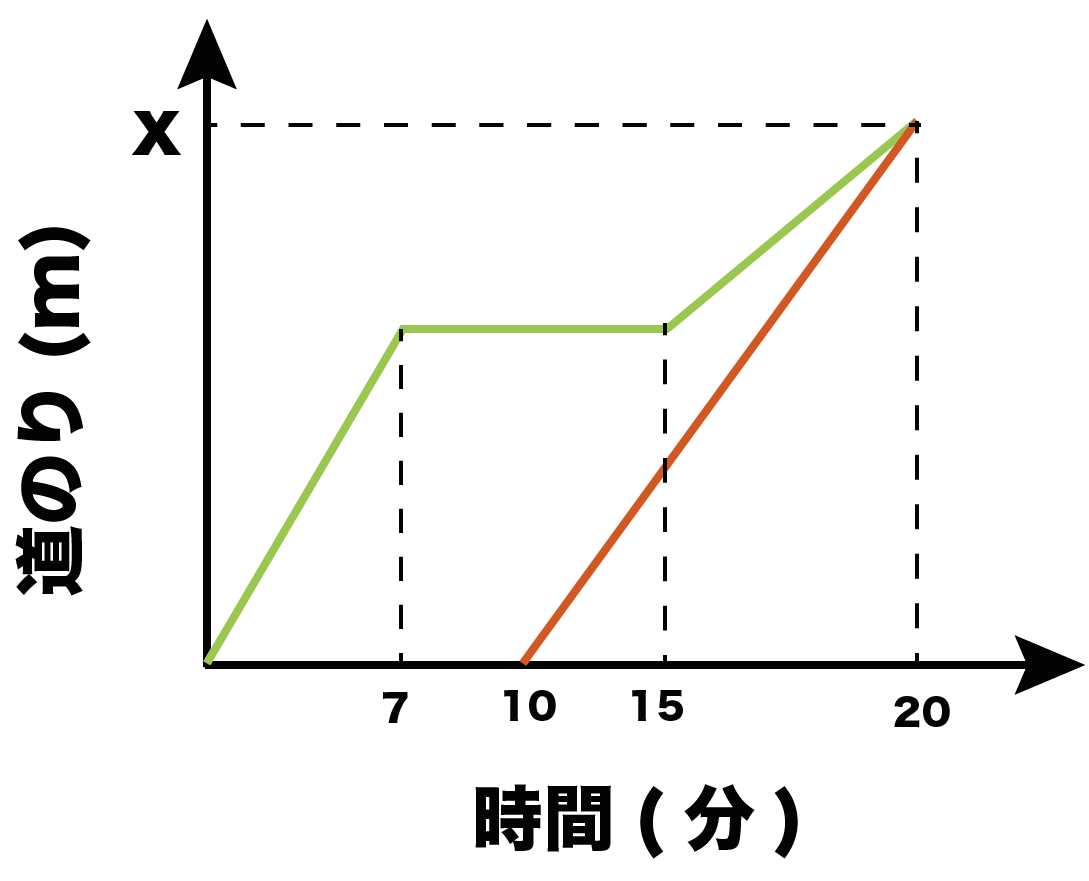
先に家をでちゃった忘れん坊の弟を、ねえちゃんがチャリで追いかけるっていう文章題だよ。
時間と道のり、っていう2つの軸が入ったグラフ・図を書いてあげると速さの問題はグンとわかりやすくなるよ。
文章題が苦手だと思ったら試してみてね。
ここまでざーっと方程式の文章題(速さ)のコツをみてきたね。どうだったかな?? ちょっと解けそうな気がしてきた??
「速さ・時間・道のり」がよくわからん!
ってときは上で紹介した記事を読んでみてねー!!
そんじゃねー。
Ken
こんにちは!皮膚科にかかっているKenだよ!
中学1年生で「比と比例式」を勉強しなくちゃなんないよね?! 正直だるいし、方程式でおなかいっぱいだ。
だけど、この「比と比例式」は基本さえわかっちゃえばむちゃくちゃ楽勝なんだ。
がんばれば期末テストの得点源になったりする。
だから、今日は「比と比例式」に登場する、
「比の値」
というものは何か??ということをわかりやすく振り返ってみよう。基本さえ押さえちまえば方程式の解き方を勉強するより楽勝だよ!
「比の値」を次の3つのステップで勉強していこう!!
「比の値」を理解するためには、まず、
算数で習った「比」を復習しなきゃならないんだ。
これは「比と比例式」を攻略するために一番大切なこと。しっかりと「比」の意味を押さえておこう。
「比」とはWikipediaによると、
2つ(または3つ以上)の数の関係を表したもの
って書いてある。つまり、2つ以上の数のどっちがどれぐらい大きいのか、ということを表している便利なアイテムなんだ。
たとえば、ぼくのお小遣いが1000円。きみのお小遣いが10000円だとする。かなりもらってるね。 うらやましいよ。
このとき、「きみのお小遣い」は「ぼくのお小遣い」の10倍だね??
このお小遣いの格差を比で表してあげるとこうなる↓↓
「:コロン」をはさむだけで2つの数量を比較できるんだ。おこづかいでもテストの点数でも1500mのタイムでもなんだってありさ。
これが小学校の算数でならった「比」だよ。しっかりと押さえておこう。
次に押さえておきたいのは「比の項」だ。
さっきの「比」という用語さえ理解してればちょちょいのちょいさ。たとえばさっきの例でいえば、
1 : 10の「1」を「前の項」、「10」を「後ろの項」とよんでいるんだ。そして、両方には「比の項」っていう名前がついてる。しっかり押さえておこう。
やっとこの記事のテーマである「比の値」にたどりついたね!
じつは「比の値」はさっきまで勉強してきた「比の項」を理解してれば楽勝なんだ。
比の値とはずばり、
(前の項)÷(後ろの項)なんだ。
だからさっきの「おこづかいの比」の例でいえば、
10分の1が「比の値」になるんだ。
前の項と後ろの項の順番さえ間違えなきゃ大丈夫だね!。
ここまで勉強してきた「比の値」はよくわかったかな??
比の値をしっかりおさえて次の比例式に備えちゃおう!
そんじゃねー!!
Ken
こんにちは!この記事を書いているKenだよ。岩盤浴にハマってるんだ。
前回は「分数がふくまれる」方程式の解き方をみっちり勉強してきたよね?? これさえマスターしてまえば中1数学の方程式をクリアしたも同然さ。
ただ、分数をふくむ方程式と同時に気をつけてほしいのが、
小数をふくむ一次方程式の解き方
なんだ。
分数よりヤッカイじゃないけれど、気をつけないと間違ってしまうことが多い。だから今日は、
小数をふくむ一次方程式の解き方で気をつけるべきことを1つだけ紹介するね。
小数がはいった方程式の解き方では、
小数を消し去る
ということを初めにやっちゃえばいいんだ。
これがどういうことか説明していこう。たとえば、次のような小数をふくむ一次方程式があったとしよう。
0.3x = 0.05x + 1
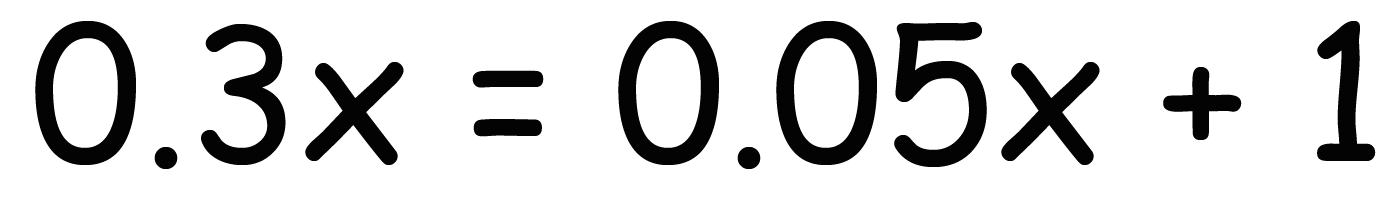
小数を消し去るためには、
一番小さい小数の位がなくなるような数を両辺にかけてやればいいんだ。
えっ。何をかけたらいいのかわからないって??
ゆっくり考えてみよう。
小数第一位の数である「0.3」には何をかけたら小数じゃなくなる??
そう、10だ。
じゃあ、小数第二位である「0.03」は??
そう、100だ。
っというように、「10を小数の位数分乗したやつ」を方程式の両辺にかけてやればいいんだ。
だから、
0.3 x = 0.05x +1
という方程式では「0.05」が一番小さい小数の項だよね?? こいつはちなみに小数第二位だ。だって、小数点より右に2つの数字が並んでるからね。
だから、
10の二乗、つまり100を方程式の両辺にかけてやればいいんだ。
30x = 5x + 100
こんな感じでスッキリした方程式に早変わりさ。
ただ、右側に注意してくれ。
ぜんぶの項に100をかけてあげないと等式が成り立たないんだ。この場合だと、「0.05x」と「1」だね。ゆっくりと解けば間違わないはずだ!
こいつを「基本的な1次方程式の解き方」を使って解いてやれば、
x = 4
という解が得られる。これで小数の方程式も楽勝さ!!
小数をふくむ1次方程式の解き方はどうだったかな??
分数の方程式よりもカンタンだったよね?? この調子で中1数学ででてくる方程式の解き方をじゃんじゃんマスターしてっちゃおう!!
そんじゃねー!
Ken
こんにちは!1日に映画を5本みたKenだよー!
中1数学で勉強する方程式はまだ可愛い方だよ。だって、文字が1つしか登場しないからね。このタイプのものは一次方程式だとか、xの方程式とかと呼ばれている。
この解き方は前回の「【中学数学】1次方程式(xの方程式)の解き方の3つの手順〜基礎編〜」で勉強したからもう大丈夫だよね??

じつは方程式でつまずく人が多いと言われているのは、
分数が含まれた方程式の解き方
を理解することなんだ。分数が含まれるとちょっと厄介。いままで楽勝に見えていた方程式がむずかしくみえちゃう。これは勉強する側としてはとても嫌。。
だから、今日は中1数学の方程式の解き方でつまずかないためにも、
分数がふくまれる1次方程式の解き方
を2つのステップで振り返ってみよう。
前回勉強したチョー基礎的な方程式の解き方を応用できるまでに、
分数の方程式ではやることが2つあるんだ。
たった2つだけ。
これさえやっちゃえばいつも通り方程式を解くだけでいいんだ。カンタンそうでしょ??
分数の方程式の解き方を説明するために、今日は、
(2x + 5)/3 = (x-4)/4
という分数入りの方程式の解き方をみていくよ!
まず最初に「分母を払う」というワザをつかって分数の方程式をシンプルにしちゃおう。
「分母を払う」とは、
分母をなくしちゃうこと。つまり、分数を方程式から消し去ろう!ということなんだ。
そのためには具体的に、
左と右の分数の分母の「公倍数」をかけてあげればいいんだ。
えっ。公倍数がよくわからない?? Wikipediaによると公倍数とは、
2つ以上の正の整数の、それらに共通する倍数のことをいう。
とあるよ。つまり、2つ以上の数字をそれぞれ何倍かずつしてやれば同じ数になる。このとき、その「同じ数になる数字のこと」を公倍数っていうんだ。
たとえば、「3」と「4」の公倍数は12。だって、「3」を4倍したら「12」になるし、「4」を3倍しても「12」になるからね。
だからさっきの例題の、
には、まず分母の「3」と「4」の公倍数12を方程式の両辺にかけてあげるんだ。等式を成り立たせるために、かならず両方に同じ数をかけてね!
そうすると、
こうなるよね??
そんで、左の分母3と、右の分母4が12によって消されちゃうので、
こうなる。
ここで注意してほしいのは分子をきっちり()でくくってやること。分母を払うためにかけた数字の残骸(ここでは赤い数字の4と3)で分子を()でくくるのさ。
これを忘れると計算結果が異なってくるので注意してね。
あ、分母の公倍数がよくわからん!
というときは分母の数をそれぞれゆっくりかけてみてもいいよ。たとえば、この例でいえばとりあえず「3」を両辺にかける。そんで、次に残った分母の「4」をかける。
これでもおk!
さて、次が一番間違いの多いところだよ。分母を払って安心しちゃう奴が多いんだ。
分母を払ったときに残った残骸で分子を包んだね???
そしたら、その()を分配法則をつかってはずしてみよう。
()の外の数字を中の数字すべてにかけるのを忘れずにね!
分配法則をつかって()をはずしてやると、
8x + 20 = 3x -12
になるよね??
この方程式のカタチはチョー基本形。だから「【中学数学】1次方程式(xの方程式)の解き方の3つの手順〜基礎編〜」で紹介した解き方を使ってやればすぐ解けるんだ。
xと数字の項を移行して分離させ、そしてxを裸にしてやると、
x = -32/5
分数をつかった方程式でやっかいになる解き方は上の2つだけでいいんだ。あとは基本的な方程式の解き方と同じ。ゆっくりやればとけそうだね。
ここまで勉強してきた分数の方程式の解き方はどうだったかな?? 分数の方程式とかむずかしそうに聞こえるけど、ちょっと手順を付け加えてやればちょちょいのちょいさ。
計算ミスをしないようにゆっくり解いてみよう!!
そんじゃねー!!
Ken
こんにちは!イボコロリを使ってみたKenだよ。
中1数学でむずかしいと言われているのは「方程式」。中1で勉強するのは「1次方程式」とよばれているものだ。なにせ、文字が1つしか含まれていないからね。
ちまたでは「xの方程式」と呼ばれているらしい。

今日は「一次方程式」の解き方の手順を3つにわけて紹介するね。
でも、中1で勉強する1次方程式にも「むずかしいもの」と「簡単なもの」があるんだ。
まず手始めということで、
今日はxの方程式の解き方の基礎的な手順を書いてみた。よかったら参考にしてみてね。
それでは簡単な1次方程式(xの方程式)の解き方を振り返ってみよう。xの方程式の具体例として、
7x-2 = 5x +10
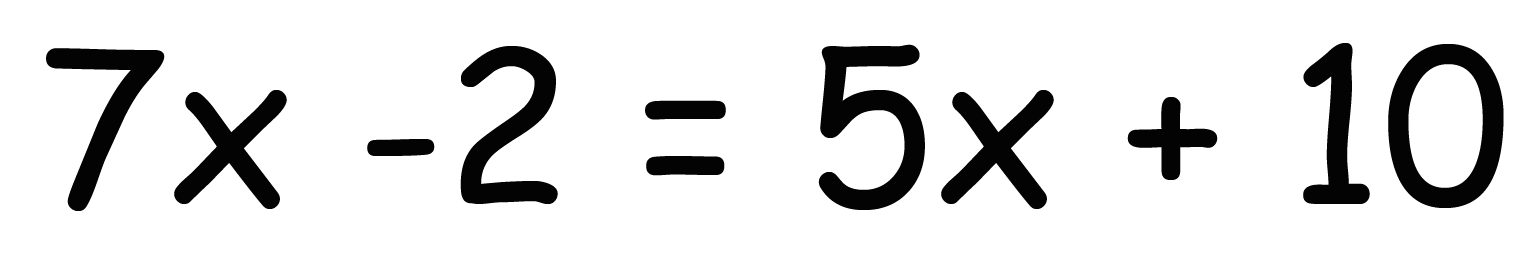
という方程式をつかって考えてみるね。
まず一次方程式(xの方程式)でやるべきことは、
等式の左に文字xの項をよせること
だ。この方程式でいえば、
「7x」と「5x」が「xの項」だよね?? だって、項の中にxが含まれているからね。
7xはもともと左にあるから、5xをがんばって左側に持ってこよう。
項を移動させるときは前回ならった「移項」というワザを使うんだ。超シンプルにいうと、移項とは「逆側に項を移すときに符号を変える」というもの。
だから、5xにマイナスの符号をつけて、コイツを左に持ってくるんだ。
これで方程式の解き方の第一ステップは終了!
次はx以外の項。つまり、数字の項を右側によせちゃおう!!
さっきの例でいえば、「-2」と「10」が数字の項だね。
右への寄せ方は手順1と同じだよ。
そう。移項というワザを使ってやるんだ。符号を変えながら数字の「-2」という項を右へ移してやるとこうなる!
左に文字、右に数字を寄せたね??
次はその寄せた項同士で計算してもっとシンプルな形に変えてやればいんだ。足し算や引き算であることが多い。
さっきの例の「左」と「右」の計算をしてカンタンな式にしてやればこうなる↓↓
2x = 12
これは俗にいう、
ax = b のカタチ
というやつさ。ここまでくれば方程式は解けたも同然。あと一歩だから踏ん張ってみよう!!
最後はxを裸にしてあげるんだ。つまり、
x = ~~~~
というように、xの項の係数をかならず1にしてあげる。これを巷では「xを裸にする」といわれているんだ。
「解き方3」から「解き方4」に移行するためには、
xの係数で左と右の式を割ってあげればいい。
たとえばさっきの例でいえば、
左のxの項の係数は2だよね。だって、xの前に2がついているから。
だから左と右の両辺を「2」で割ってみよう。するとこうなって、
最終的にこうなる↓↓
つまり、
この方程式の解は「6」ということだね! xの値が方程式の解だから当然だよね?? これで中学1年生で勉強する「一次方程式」をマスターしたも同然だ。
以上で一次方程式の解き方は終了だよ。
あくまでもこれは超基礎的な方程式の解き方。だからこれだけじゃ解けない方程式もあるよ。
だから次回は、中1数学の方程式の解き方の応用編について語っていくよ。お楽しみにー!!
そんじゃねー!!
Ken