こんにちは!この記事をかいているKenだよ。花粉に敏感だね。
3点を通る円の中心
を作図したいときってあるよね??
たとえば、つぎの問題が宿題にだされたときとかね ↓↓
例題
下の図のように、1直線上にない3点A, B, Cを通る円の中心を求めなさい。

見た目むちゃくちゃむずそう。。
だけど、基本をおさえちまえばサクっと作図できちゃうんだ。
今日はこの、
3点を通る円の中心の作図・書き方
を3ステップで解説していくよ。
よかったら参考にしてみて。
3ステップでかけちゃうよ。
作図につかうのは、
の2つだけだね。
例題をといていこう!
例題
下の図のように、1直線上にない3点A, B, Cを通る円の中心を求めなさい。

まず弦をかこう。
隣り合った2点を直線でむすべばいいんだ。
例題でいうと、
だね??
こいつらを直線でむすんでやると、こうなる↓↓
この直線たちが円の弦になるんだ。
2本ひけばステップ1完了!
つぎは弦の垂直二等分線を作図しよう。
垂直二等分線を2本かけばいいんだ。
えっ。垂直二等分線の作図方法わすれた??
そのときは垂直二等分線の書き方を復習してみて。
例題でいうと、
まず点Aにコンパスの針をおいて半円をかく。
コンパスの脚の幅をキープしたまま、
今度は点Bに針をおく。
そして、半円をかく。
2つの半円の交点をむすぶと、点A・Bの垂直二等分線のできあがり!
今度は弦BCの垂直二等分線。
てきとうにコンパスの脚をひらいて、点Bに針をおこう。
そして、半円をかく。
脚の幅をキープして点Cに針をおく。
そして、半円をかく。
おなじように半円の交点をむすべばいいのさ。
それが垂直二等分線になる。
どう??
垂直二等分線かけたかな??
最後は交点をうつだけ。
垂直二等分線がまじわっているところに、
ぽちっと点をうてばいいんだ。
その交点が「3点を通る円の中心」になるよ。
例題でもおなじ。
垂直二等分線の交点をうってやろう。
すると、こんな感じになる↓↓
おめでとう!
この交点が「3点を通る円の中心」だよ。
でもさ、
なんで「三点を通る円の中心」がかけちゃうんだろう???
都合よすぎるよね。
その理由はずばり、
「垂直二等分線上の点」と「端の点」同士の距離が等しいから
なんだ。
例題の円の中心をOとすると、
AO = BO = CO
になるってわけ。
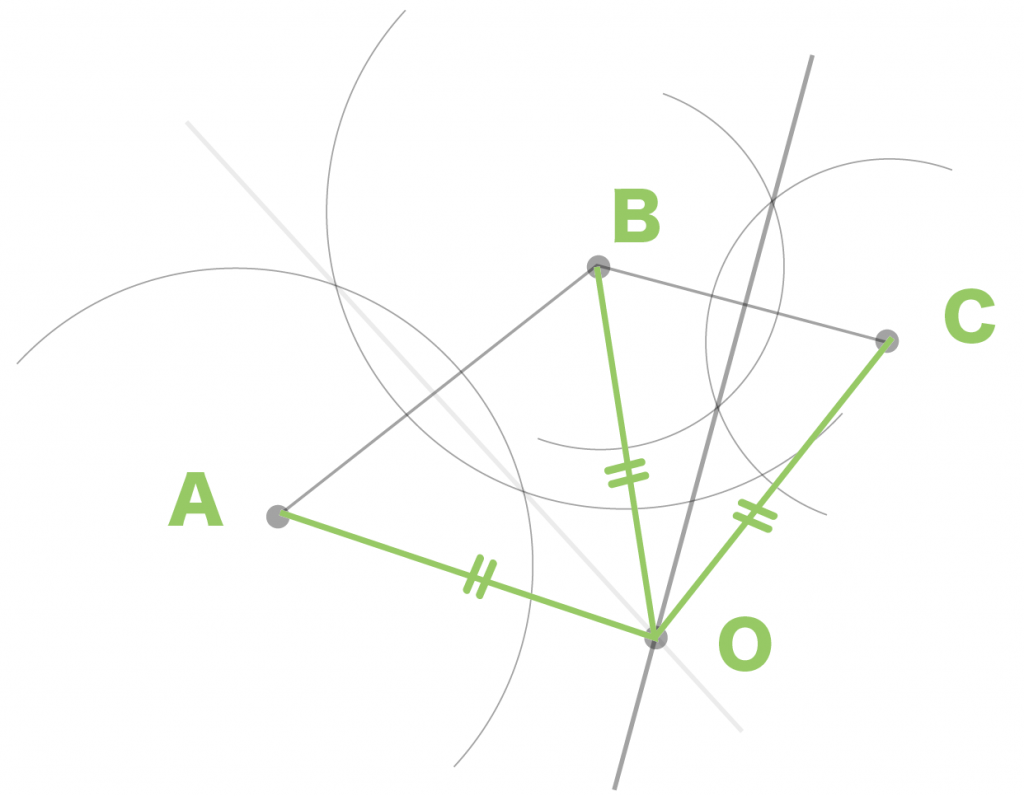
つまり、
点A, B, Cたちは点Oからの距離が等しいってことだね。
円の定義は「ある点から等しい距離にある点の集合」だから、
3点を通る円が点Oを中心にかけちゃうってわけ。
えっ。なぜ、
「垂直二等分線上の点」と「端の点」同士の距離が等しくなる
のかって?!?
それは、垂直二等分線をかいてみればわかる。
たとえば線分ABの垂直二等分線をかいて、二等分線上の点をOとしよう。
ABと垂直二等分線の交点をMとするよ。
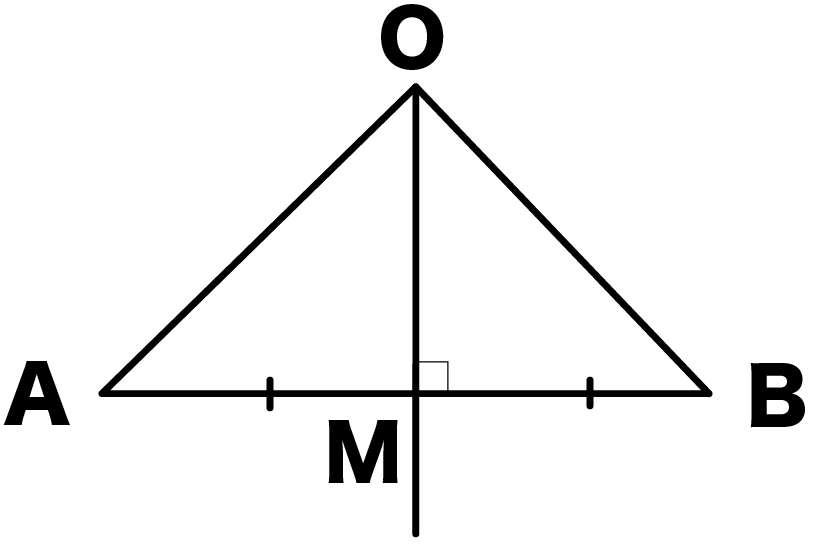
このとき、OMは垂直二等分線だから、
になる。
しかも、OMは共通だから、
2辺とのその間の角がそれぞれ等しい
という合同条件がつかえるね。
よって、
△AMO ≡ △BMO
になるわけだ。
対応する辺の大きさが等しいから、
AO = BO
になるんだ。
どう??納得いったかな??
三点を通る円の中心をかく
ってむちゃムズそう。
ただ、使うのは、
垂直二等分線だけ。
慣れてしまえば簡単なんだ。
テストまでに作図の練習をしてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。カレーはグリーンに限るね。
中学数学の問題でたまーに、
コンパスと定規で正方形を作図しなさい
ってやつでてくるよね??
三角定規と分度器をつかえば楽勝。
正方形なんてかける。
だけど、
コンパスと定規だけしかダメ??
そりゃあ、ムズい作図になるね。
今日は、作図を攻略するために、
正方形の書き方・作図方法がわかる5ステップ
を紹介するよ。
よかったら参考にしてみてね。
正方形はつぎの5ステップでかけちゃうよ。
作図に用意するものは、
の2つだけ。
さあ、正方形をかいていくよー!
まず直線をかこう。
定規でまっすぐ線をかけばいいんだ。
これが第1ステップ!!
つぎは直線上で円をかいてみよう。
適当にコンパスの針を直線上におく。
まるっと円をかけばいいんだ。
これが第2ステップ!!
つぎはチョビ円を2つかくよ。
コンパスの脚をちょっと広げて、
円と直線の交点に針をおこう。
そんで、チョビっとだけ円をかく。
もう一個の交点でもおなじ。
チョビっと円をかいてね。
これで第3ステップ終了だね!
チョビ円の交点と、
円の中心を直線でむすんであげよう。
これは直線の垂線になっているね。
詳しくは「垂線の書き方」の記事をよんでみて。;
「円」と「直線」の交点をむすぼう。
むすんでできた図形が正方形になってるよ。
おめでとう!
正方形の書き方もマスターだね。
でもさ、
なんで正方形が作図できちゃうんだろう??
簡単すぎてこわいよね。
じつは、
4つの直角三角形が合同だからいえるんだ。
たとえば、角交点を下の図のように、
とおいてあげよう。
すると、
△ABO ≡ △BOC ≡ △COD ≡ △DOA
になるね。
んで、
合同な図形の対応する辺・角はそれぞれ等しいから、
がいえそう。
これは、正方形の定義の、
4つの辺がすべて等しく、4つの角がすべて等しい
をみたしているね。
だから、四角形ABCDは正方形になるんだ。
どう??納得したかな??
正方形の書き方はどうだったかな??
の5ステップだけでいいんだ。
コンパスと定規しか使わない。
なんだかいけそうな気がするでしょ??
練習して書き方になれていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鮭を2匹やいたね。
正三角形を作図したい。
そんなときってたまに、ある。
宿題にでてしまったり、
正三角形を落書きしたくなったりしたときにね。

今日はそんな身近な、
正三角形の書き方・作図方法を3ステップで解説していくよ。
よかったら参考にしてみて。
使うものは「コンパス」と「定規」。
こいつらがあれば、
どんな正三角形だってかくことができる。
むちゃキレイにね。
今回はいっしょに、
1辺が6cm の正三角形ABCをかいていこう!
書き方はつぎの3ステップさ。
まず使うのは、
定規、きみだ。
定規をつかって、
正三角形の1辺をひいてみよう。
定規に沿って、
すーーーっと線をかくだけでいいんだ。
1辺が6cmの正三角形をかきたいんだったら、
6cmの線分をかくだけさ。
線分の両端をA・Bとおこうか。
これが第一ステップさ!
つぎは、コンパスの出番。

コンパスで、
半々円を2つかいてやろう。
半半円とは、半円の半分のやつのこと。
つまり、
1つの円の4分の1サイズのやつさ。

そいつを、
さっきかいた線分の両端を中心にして、
かいてやればいいんだ。
1辺が6cmの正三角形のときも同じ。
まず、線分の端のAに針をおこう。
んで、
コンパスの鉛筆を逆のBにおく。
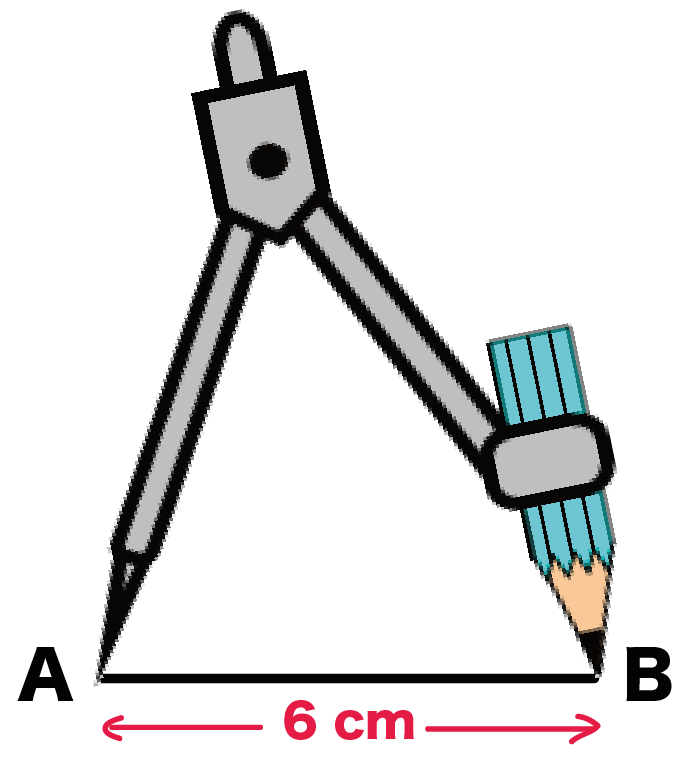
そして、
半半円をかく。
そのつぎは、逆のBにコンパスの針をおいて、
鉛筆をAにおく。
そして、
半々円をかく。
これで第二ステップは終了さ!
あとは、半半円の交点と線分の両端をむすぶだけ!
半々円たちの交点をCとしよう。
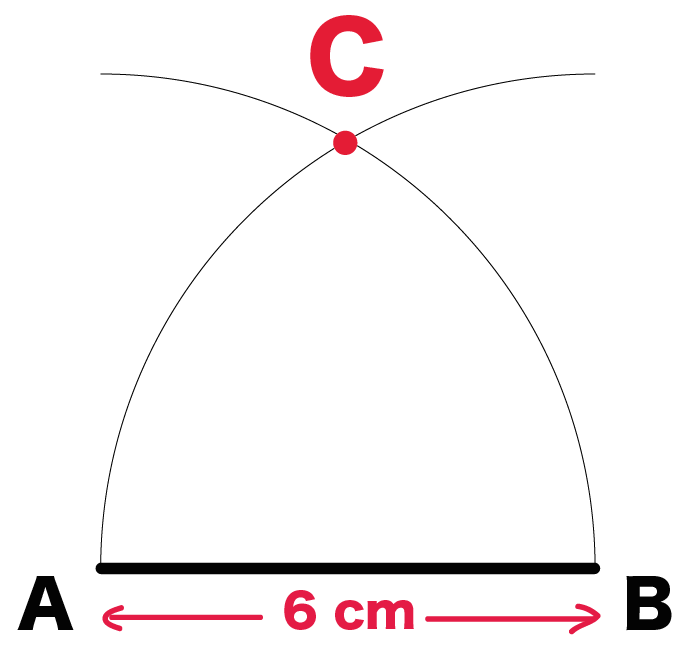
この交点Cと、
両端のA・Bを直線でむすべばいいんだ。
定規でむすんでみると、
あら!
正三角形ABCのできあがり!
正三角形をかきたい。
そんなときは、
コンパスと定規をさがそう。
そして、
使おう。
あとはゆっくり作図すれば大丈夫。
何度も練習してみてね。
そんじゃねー
Ken