こんにちは!この記事をかいているKenだよ。カラオケもいいね。
中2数学でh「式の値」っていうやっかいなヤツがでてくる。
「式の値」の問題って、
文字式の中の「文字」に数字をいれたときの値を求める
っていうやつなんだ。
文字に数字をいれて計算するだけ!
慣れれば簡単だからガンガン点をとっていこう。
今日は中2数学ででてくる、
「文字が2つ以上登場する」式の値の問題
を解説していくよ。
よかったら参考にしてみて。
さっそく「式の値」の解き方をみていこう。
つぎの例題をといてみよう!
a = 3/2、b = -2/17のとき、次の式の値を求めなさい。
(8a + 3b) -2(3a-7b+1)

この手の問題は3ステップでちょちょいのチョイさ。
文字式を簡単にしてあげよう!
チョー簡単な式はそのままでいいんだけど、
()のついた式はもう少しシンプルにしちゃおう。
例題の文字式をみると、
(8a + 3b) -2(3a-7b+1)
って感じで()で文字式が太っているよね??
とてもじゃないけどスリムなんかじゃない。
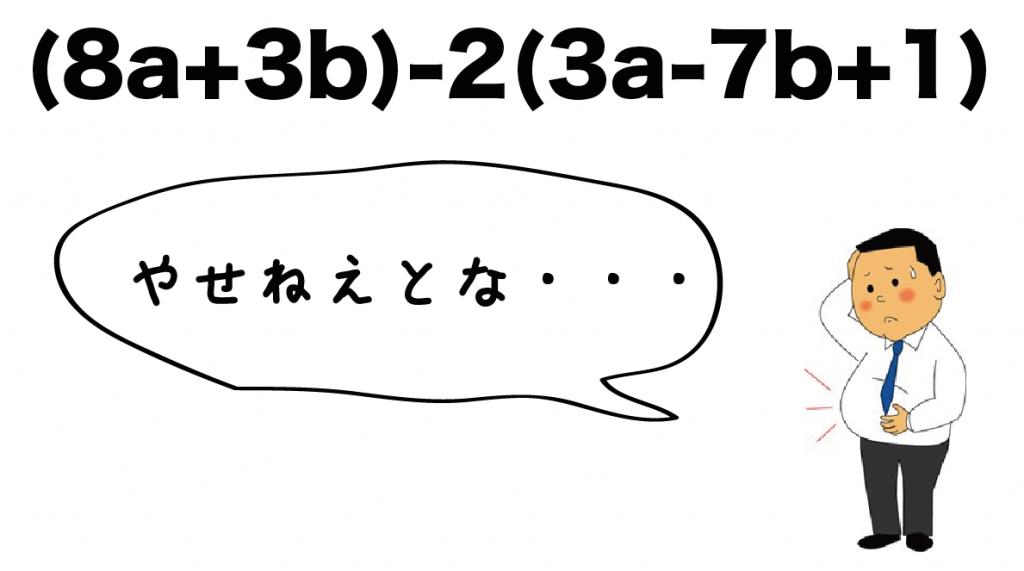
(8a + 3b) -2(3a-7b+1)
をスリムにするために分配法則をつかってあげよう。
すると、
(8a + 3b) -2(3a-7b+1)
= 8a + 3b -6a + 14b -2
になるね!
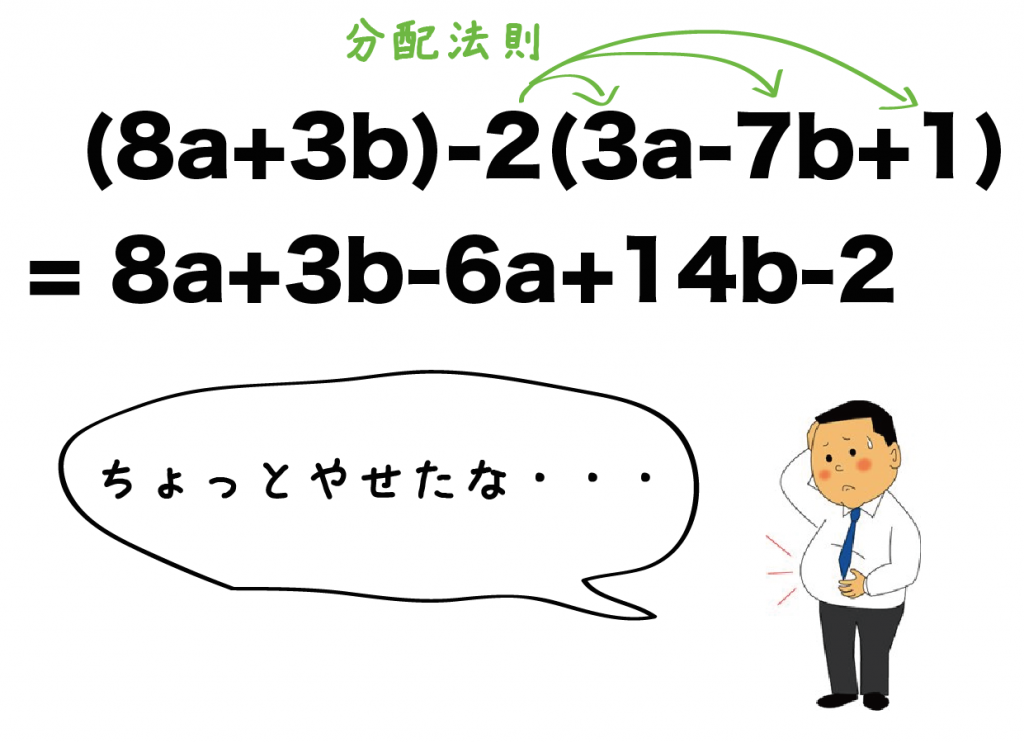
どう??だいぶスリムになったよね?。
文字式の()をはずしただけじゃまだスリムじゃない。
式は横に長いし、どうにかしてあげたくなるよね?。
つぎはもっとシンプルにするために、
同類項をまとめる
っていう荒技で勝負してみよう。
例題でちょっと簡単にした、
8a + 3b -6a + 14b -2
という式にはつぎの3種類の項があるよね?
同じ文字の項は係数をたしてみよう。

すると、
2a +17b -2
って感じで文字式がスリムになったでしょ??
最後に文字に数字を代入してみよう。
どんな数字を入れればいいのか
ってことは問題にかいてあるよ。
この例題では、
って問題で指定されているよね?
こいつらをStep2で計算した超スリムな文字式に代入してあげよう。
すると、
2a +17b -2
= 2 × 3/2 + 17×(-2/17) -2
= 3 + (-2) -2
= -1
っていう式の値が求まるね!
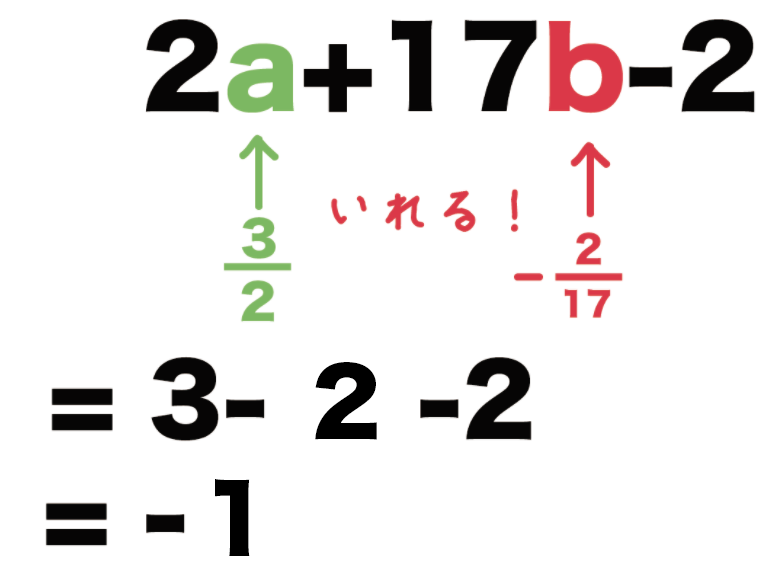
おめでとう。これで「式の値」もマスターしたね。
式の値を求める前には必ず、
文字式をできる限りカンタンにする
ってことを忘れずにね!
これなら焦らずに式の値を計算できるはず!
テスト前にもう一度復習してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。我が家にたんすが来たね。
「同類項」って、
「文字」と「次数」が同じ項たちのこと
なんだ。
つまり、
同じ英文字を使っていて、なおかつ、その文字が何回かけられているかが一緒
の項たちってことさ。
たとえば、
a²-2a-3a+4
っていう多項式があったとしよう。
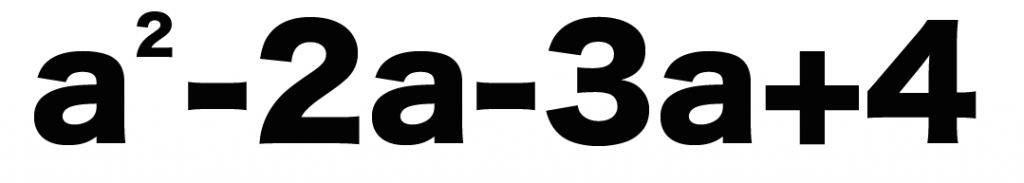
この多項式にはぜんぶで4つの項があるけど、
「文字」と「次数」が同じなのは次の2つだね。
この2つの項が同類項ってことになる。

そんで、中2数学の「式の計算」っていう単元では、
同類項をまとめる
っていうワザをマスターしていないといけないんだ。
今日はその「同類項のまとめ方」をわかりやすく3ステップで解説していくよ。
同類項がどうしてもまとめられん!ってときに参考にしてみてね。
「同類項をまとめる」ってつまり、
2つ以上の同類項を1つの項にするってこと
だ。
その「同類項のまとめ方」は3ステップでできちゃうんだ。
つぎの例題をときながらみていこう。
つぎの式の同類項をまとめてね。
2a + 7b – 2a² + + 8c + a³ – 6a²
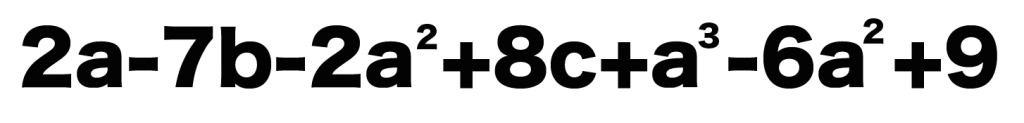
まずは同じ「文字」が使われている項をさがしてみよう。
つまり、同じアルファベットの文字をみつけるってわけ!
あ、数字の項は「数字」っていう文字だと思っていいよ。
例題の、
2a + 7b – 2a² + + 8c + a³ – 6a²
を3秒ぐらいみつめていると、
っていう4つの項に同じ「a」っていう文字が含まれていることに気づくよね。

だから、まずはこいつらが、
同類項である疑いが高い項たち
ってことさ。コナンでいえば、いかつくて犯人っぽいキャラみたいな感じだね。
つぎは「次数」が同じ項だけを抜き出してみよう!!
「次数」が同じってことは、
その文字がかかっている回数が同じ
ってことだね。つまり、
何乗されているか?ってことが一緒ならいいんだ。
例題をみてみよう。
さっきの「同じ文字の項たち」のうち、次数が同じやつは、

の2つだね。こいつらは文字も一緒だし、次数も同じだ。
だから同類項ってわけ!!
最後に、同類項たちをまとめちゃおう。
まとめ方はいたって簡単。
同類項の係数を足し合わせるだけでいいんだ。
係数って「文字式」の「文字じゃない部分」
のことだったよね??
例題をみてみよう。
っていう2つの項の係数はそれぞれ、
だ。こいつらを足しあわせてやると、
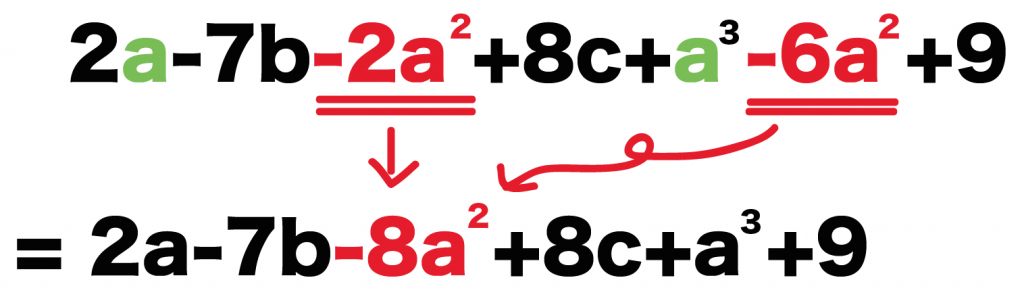
-2 + (-6) = -8
になるはず!!
係数じゃない文字の部分はそのままにしていいので、
例題の式の同類項をまとめると、
-8a²
になるね。
おめでとう!これで同類項をまとめられたね。
同類項のまとめ方はどうだった??
っていう3ステップで完了なんだ。
テスト前にもう一度確認してみてね。
そんじゃねー!
Ken

中2数学の「式の計算」で押さえたいことは、
「単項式」と「多項式」の違い
だね。この2つはごっちゃにしやすい数学用語なんだ。
だって、「単項式」と「多項式」って漢字で1文字しか違わないし、

ひらがなに直しても1文字違いだからね。

当然、勉強していると、
単項式と多項式をごっちゃまぜにする
という事態におちいるわけさ。
今日は、そんなミスをなくすために、こんな記事をかいてみたよ。
その名も、
3分でわかる!単項式と多項式の違い
さ。「単項式」と「多項式」の違いがわからないときに参考にしてみて。
「単項式」と「多項式」ってどっちも、
「文字」と「数字」でできた式
のことなんだ。

それで、こいつらにはこんな違いがあるんだ。
つまり、
「かけ算」だけできた文字式は「単項式」、
「かけ算」と「たし算」で成り立つ文字式は「多項式」ってことになるね。

それじゃあ、単項式と多項式をそれぞれ詳しくみてみよう!!
改めてもう一度復習だね。
単項式って、
「かけ算のみ」で表される「文字」と「数」の式のこと
なんだ。
たとえば、「5a」っていう式は単項式だね。

なぜなら、
「5」という数字と「a」っていう文字が「かけ算のみ」でつながっているからね。
また、文字だけの「p」っていう式も「単項式」だし、
数字だけの「5000」っていう式も単項式だ。
だって、なにもかかっていないように見えても
「1」がかけられているからね。
足し算が含まれていなければ単項式になる
ってことを覚えておこう!
多項式とは、
「かけ算」と「足し算」でできた「文字と数字の式のこと」
を言うんだ。
たとえば、
2a+7

とか、
a^2 + 3abc + 7
とかね。

もっといっちまえば、
単項式を+でつなげたもの
ともいえる。

だって、多項式の中の1つ1つの項は単項式になっているからね。
さっきあげた例でいうと、
「a^2」「3abc」「7」はすべて単項式
だね。

単項式を足し算で結ぶもの。
それが多項式だ!!
ただ、1つだけ多項式で注意すべきことがあるんだ。
それは、
「引き算」が含まれている文字式も多項式
ってことさ。
たとえば、
7a -9
なんかね。その理由は、
「-」は「-の項をたす」って解釈できるからだよ。

引き算ではなく、「−の項」を足しているってすればいいんだ。
−が含まれる単項式の集まりも多項式である
ってことを忘れずにね。
単項式と多項式の違いはどうだったかな??
発音はすげえ似てるけど、
単項式と多項式は「たし算」を含むかどうかが違う!

って覚えておこう。
そんじゃねー!
こんにちは!この記事を書いているKenです。昼飯に焼き肉を食べました。
分配法則 (distributive property) という計算法則をご存知ですか?! 名前が超カッコイイこの法則は、中学1年生の数学でで登場します。
はじめてこの数学用語をみかけた中学生の方は、
は?? 分配??? お、おれの財産は渡せねえよう!
とぶっきらぼうになってしまうかもしれません。そんな一見、超うさん臭い「分配法則」くんですが、じつは中学校の数学の中で、かなりかなりの重要度を誇っています。
分配法則さえマスターすれば中学1年生の数学の大半を倒せます。中学1年生から数学の問題を倒せる武器を所持できるなんてうらやましいですね、まったく!

分配法則という武器を使いこなせ!!
今日はせっかくなので、
分配法則という最終兵器の概要を説明しながら、あまり知られていない便利な使い方まで紹介していきます。
分配法則の使い方がわからなくて悩んでいる方は参考にしてみてくださいね。
分配法則をわかりやすく説明してくれたら欲しいものあ・げ・る
と美女に迫られたとしましょう。なんとしても欲しいものを手に入れたいぼくは、分配法則を次のように説明するかもしれません。それは、
分配法則とは、たし算とかけ算の橋渡しの法則のことだね。
と。たぶん、こんなきざな台詞を使えば、美女も・・・・・
なんて妄想はさておき。なぜ分配法則が「たし算とかけ算の橋渡しの法則」になるのか確認していきましょう!
分配法則は中学数学の教科書で以下のように説明されています。
a, b, cという3つの数字による計算式があったとしましょう。分配法則を使うとこの文字式は次のように書き換えることができます。
$$a\times(b+c)=a\times b+a\times c$$
です。えっ。文字ばっかりで分かりづらいですって?!? そんな方のために実際の数字で分配法則を考えてみましょう。上のa, b, cを4、5、6という数字で置き換えてみると、
となります。
左の計算式を右のようにべつの形で書き換えられるわけです。このように左辺から右辺に式を変更することを分配法則を使っちゃる、といい、ちまたでは「カッコをはずす」なんて異名で呼ばれています。
まとめると、
計算式の()をなくせる法則を「分配法則」と呼んでいるわけです。
分配法則が便利なケースっていったいどんな場合でしょう??
さっきの説明では全然分配法則が役に立つ気配ありませんよね??? むしろ足を引っ張っているような気がします。
たとえば、先ほどの例であるでは余計に左辺の式を複雑にしています。なんだろう、このままでは分配法則なんて消え失せろなんて言われそうです。
そこで、読者の方が分配法則に惚れ直すことを願い、分配法則がむちゃくちゃ効力を発揮しているケースを紹介していきます。
分配法則が役に立つケースの1つとして挙げられるのは、
「桁数の大きい数字」×「1ケタの小さい数字」という計算
です。たとえば、
のような計算式。この2ケタ×1ケタ数字のかけ算は、そろばんを習っていないと瞬殺できません。ぼくはそろばんを習っていないので、この計算を終了させるのに5分ぐらいかかりそうです。えっとお、小学校で勉強した筆算の方法を利用して、

なんて感じです。じつは小学校で勉強した通りに筆算の公式を利用せずとも、この計算を瞬殺する方法があるんです。それは、
分配法則をつかって桁数の大きい数字をばらしてあげる
という方法です。えっ? どういうことなのか意味不明ですって!??
それでは詳しくわかりやすく説明していきましょう。
まずは桁数の大きい数に注目します。という計算式でいえば、
がそれに値します。
このときのポイントは、
きりのいい桁数でわけわけする
ことです。つまり、14の場合ですと、10がきりのよい桁数です。14を「10と4が足された数字」と捉え直してやるわけですね。
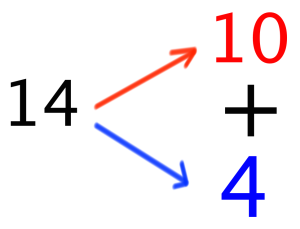
すると、という計算式は、
という()を含む計算式に変化させることができます。
桁数の大きい数字をたし算の計算式に変換したら、分配法則の出番です。記事の初めで学んだ「分配法則」をつかって式中の()をはずしてやると、
となります。え?余計に計算過程が増えてしまったですって!?? た、たしかにその感は否めません。だがしかし、の前の項の
という計算はえらくカンタンです。なぜなら、10を7にかけるだけですからね。すると、
と答えを導くことができます。14を(10+4)に変形して分配法則で()をはずす。これだけで難しい桁数の大きいかけ算もとけることになります。
この分配法則の活かし方は桁数が増えても同じです。たとえば、といった具合にです。この3ケタと1ケタのかけ算にも分配法則を適用してやると、
という感じになります。やりましたね!
それじゃあ、なぜぼくは分配法則を「橋渡し法則」と呼んでしまったのでしょうか!? さっきまでの説明に橋なんて1個も登場しませんでしたね。これじゃあ、嘘をついた罪で逮捕されそうです。
先ほどの計算式をよーーく見つめてみてください。
これです。これ。
この数式を長いこと見つめていると、
分配法則により、かけ算が足し算になったり、足し算がかけ算になったりしている、
ということが分かります。
14という数字を(10+4)というたし算の形にしたり、を
という足し算とかけ算が混じる計算式に変換したりと大忙しです。ま、まさに、分配法則は「たし算とかけ算の橋渡し法則」ですね!
それでは、また今度です!
Ken