こんにちは、この記事を書いてるKenだよー! 香港ケーキにはまってるよ。
立体の展開図の問題ってむずかしいよね??
立体をきりひらいた後、どうなるのか想像しないといけない。
これはマジで、ツラい。
展開図を作図するとチョコレートを食べたくなるねw

そこで、今日は、
3つのステップで「円柱の展開図の書き方」を解説していくよ。
円柱の展開図をかきたいときに参考にしてみてねー
円柱の展開図の書き方を紹介していくよ。
つぎの例題をみてみよう!
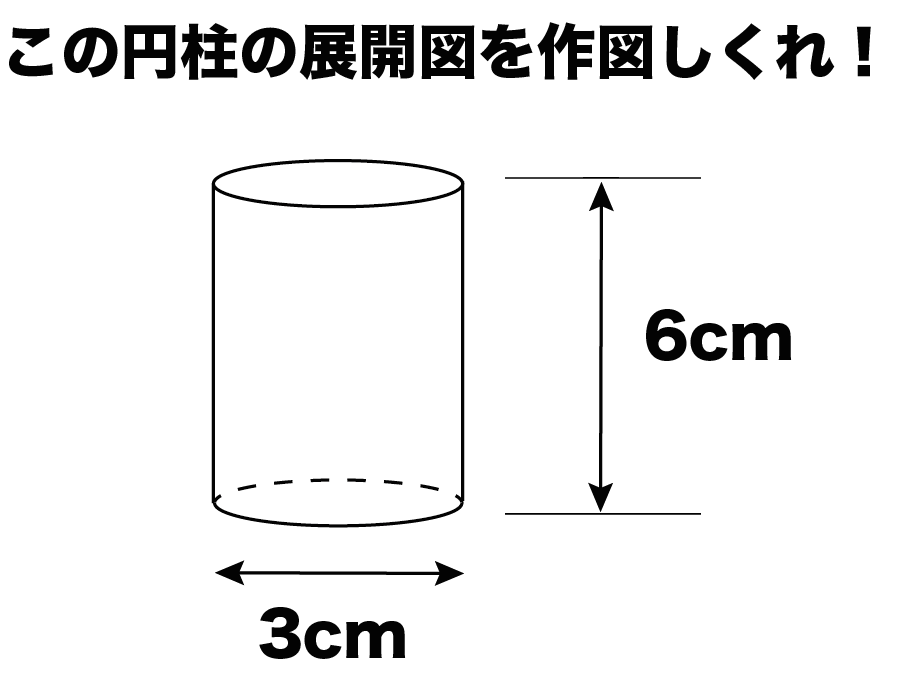
円柱の展開図は3ステップで作図できちゃうんだ。
円柱の底面は「円」だよね??
こいつの「円周の長さ」を計算しちゃおう!
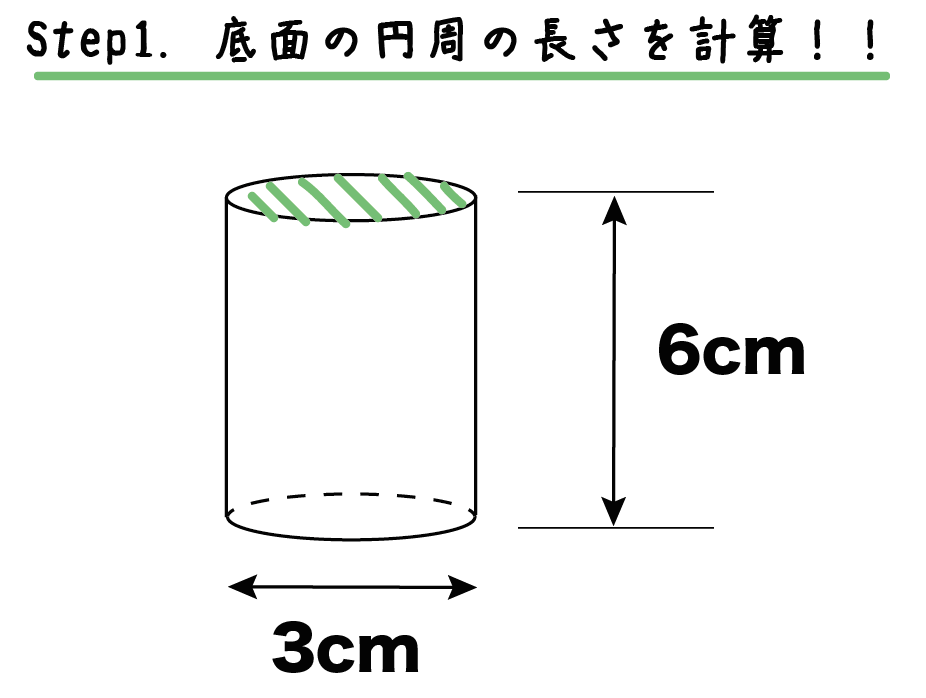
直径×円周率
だったよね?? だから、底面の「円周の長さ」は、

3π [cm]
になるよ!
つぎは、長方形をかいてあげよう。これは円柱の側面の展開図になるんだ。
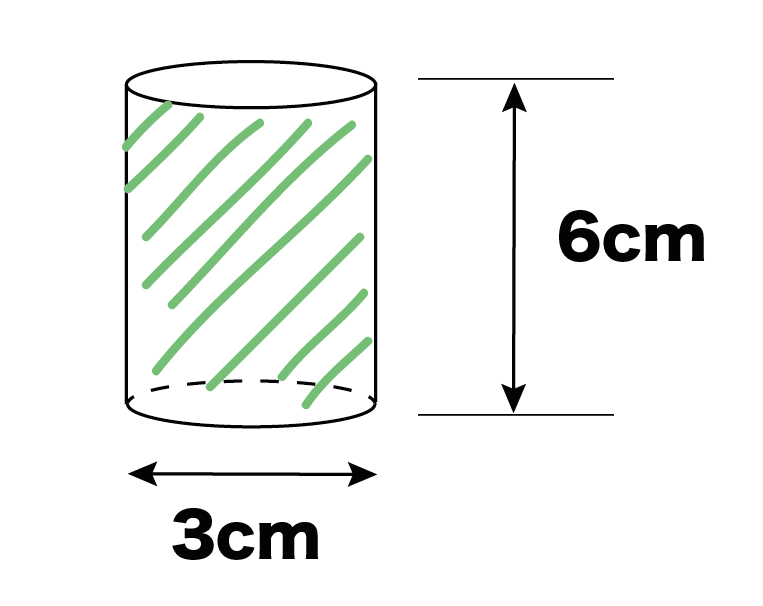
この長方形の横は「底面の円周の長さ」、縦の長さは「円柱の高さ」にしてあげよう。

さっきの例題でいえば、
円周の長さが「3π (≒9.42cm)」、円柱の高さが「6cm」だったね??

πを約3.14として作図してみるとこうなるよ。
あとは、長方形に円を2つ添えるだけ!
さっきの長方形のうえに、
ポンっと円を2つ上と下にかいてやればいいんだ。
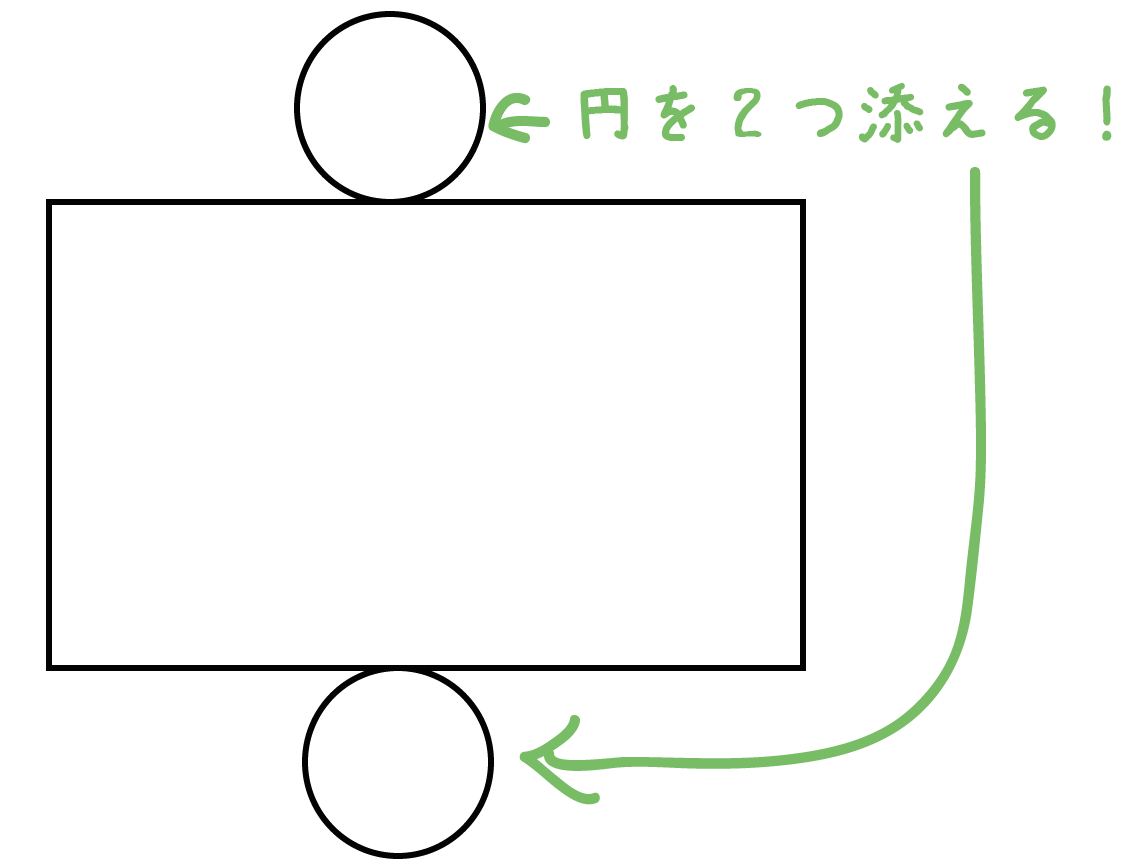
上の図みたいに、2つの円の位置が上下そろっていたほうがキレイ。
だけど、こんな感じで、ずらしも構わないし、
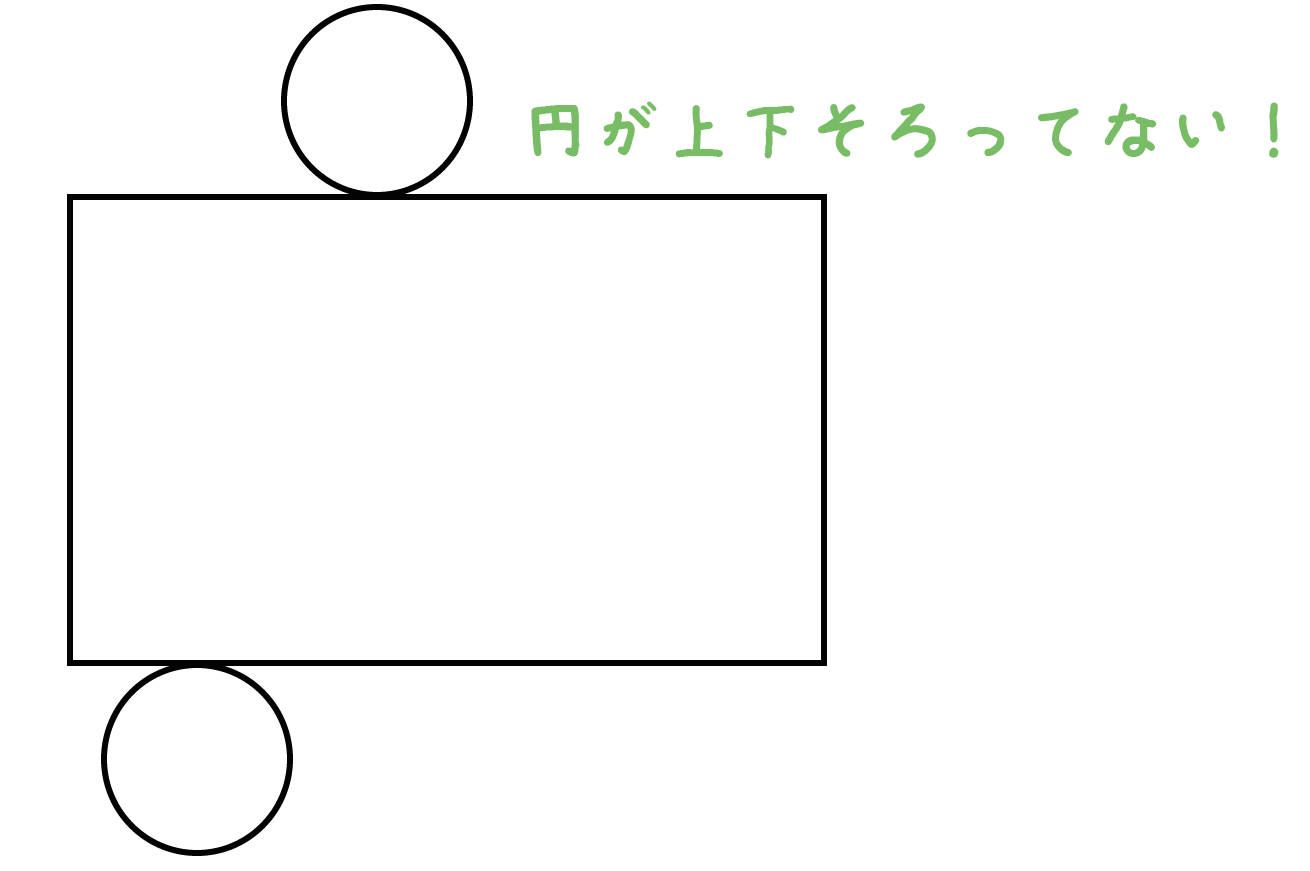
あえて両極端に円を配置してもいいんだ。
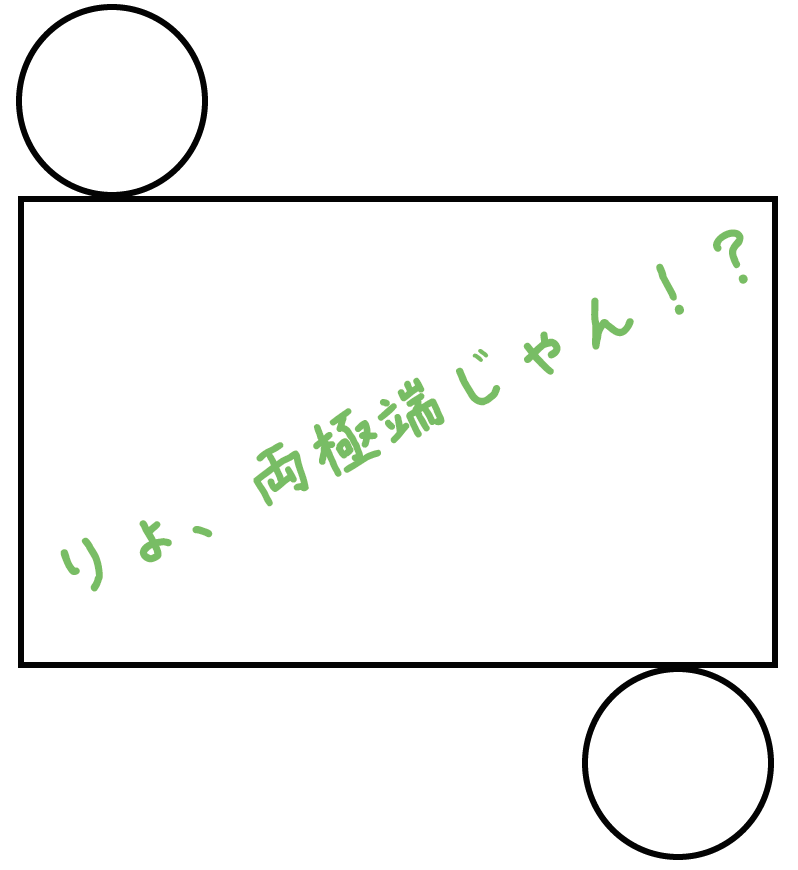
それより重要なのは、
「円」と「長方形の辺」が1点で「接している」ということなんだ。
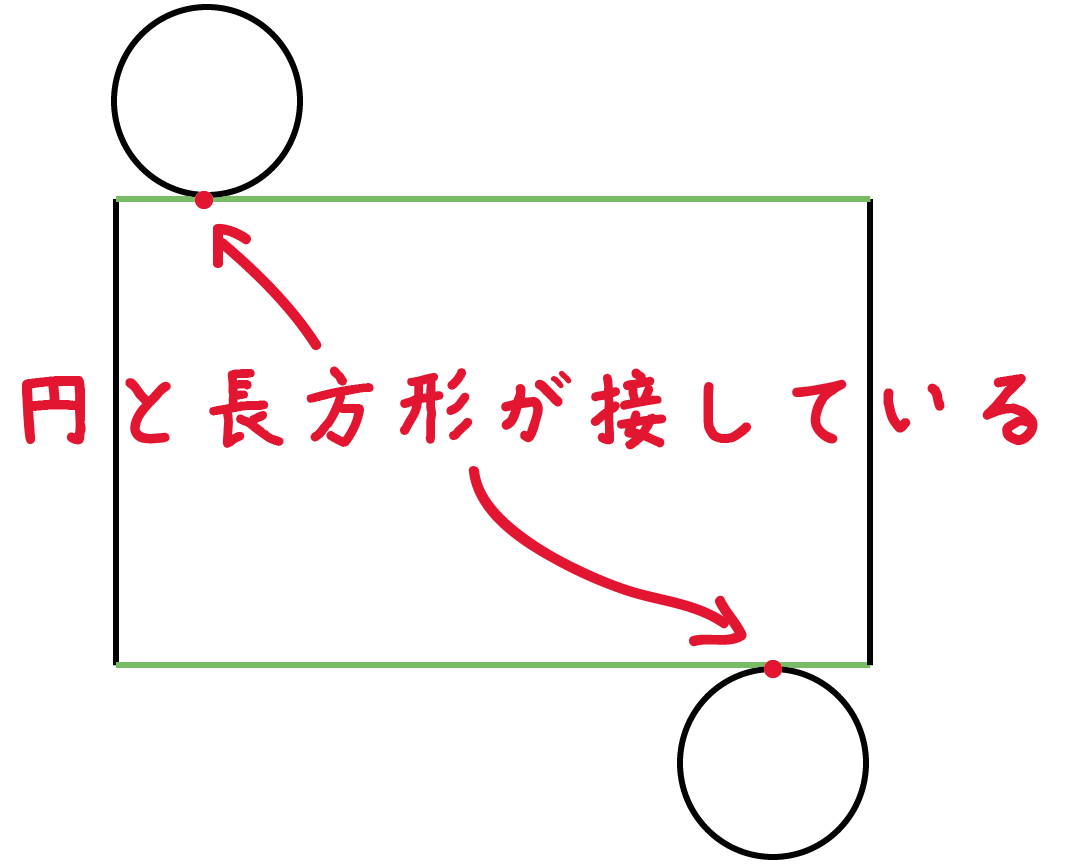
コンパスで接している円をかいてあげよう!
円柱の展開の書き方はオッケーかな??
の3ステップだったね。
展開図のかきかたをマスターしたら「円柱の表面積の求めかた」もついでに習得してみよう。
そんじゃねー
Ken
こんにちは、この記事をかいてるKenだよ。ベンチプレスにはまってるね。
中1数学の空間図形をいよいよ勉強していくよ。ここではおもに、
3次元の立体の図形
について学習していくんだ。
いままで二次元の図形とたたかってきたよね。これからは立体図形を相手にしていくんだ。
おっしゃああ!!
って気合いで教科書を読んでいると、
とにかく、
「立体図形の名前とか種類」が多すぎっ!!!
って思わない??

だから、今日は、
中1数学の「空間図形」に登場する立体の種類・名前10のまとめ
っていう記事をかいてみたよ。「立体の名前」を整理したいときに参考にしてみて。
〜もくじ〜
まず押さえておきたいのは、
球(きゅう)
という立体だ。

「球」とは算数用語集によると、
空間において,ある定点から等距離にある点の集まりを球といいます。
ってあるね。
つまり、球の中心から360°距離の等しい点をあつめまくった立体ってことだね。だから、中心から球の表面までの距離はすべて等しいよ。
ちょっと分けわかんないときは、「球」を丸いボールと思っちゃえばいい。

うん、そこらへんに転がっている「野球ボールみたいな立体」さ。
つづいては、
名前に「柱(はしら)」がつく空間図形だ。
通称、柱系の立体図形さ。
柱系の立体図形は、ただ単にそこらの「柱」と似ているってだけじゃない。
「2つの底面」が同じ形をしていて、なおかつ、「側面の図形」が四角形である立体のこと
なんだ。
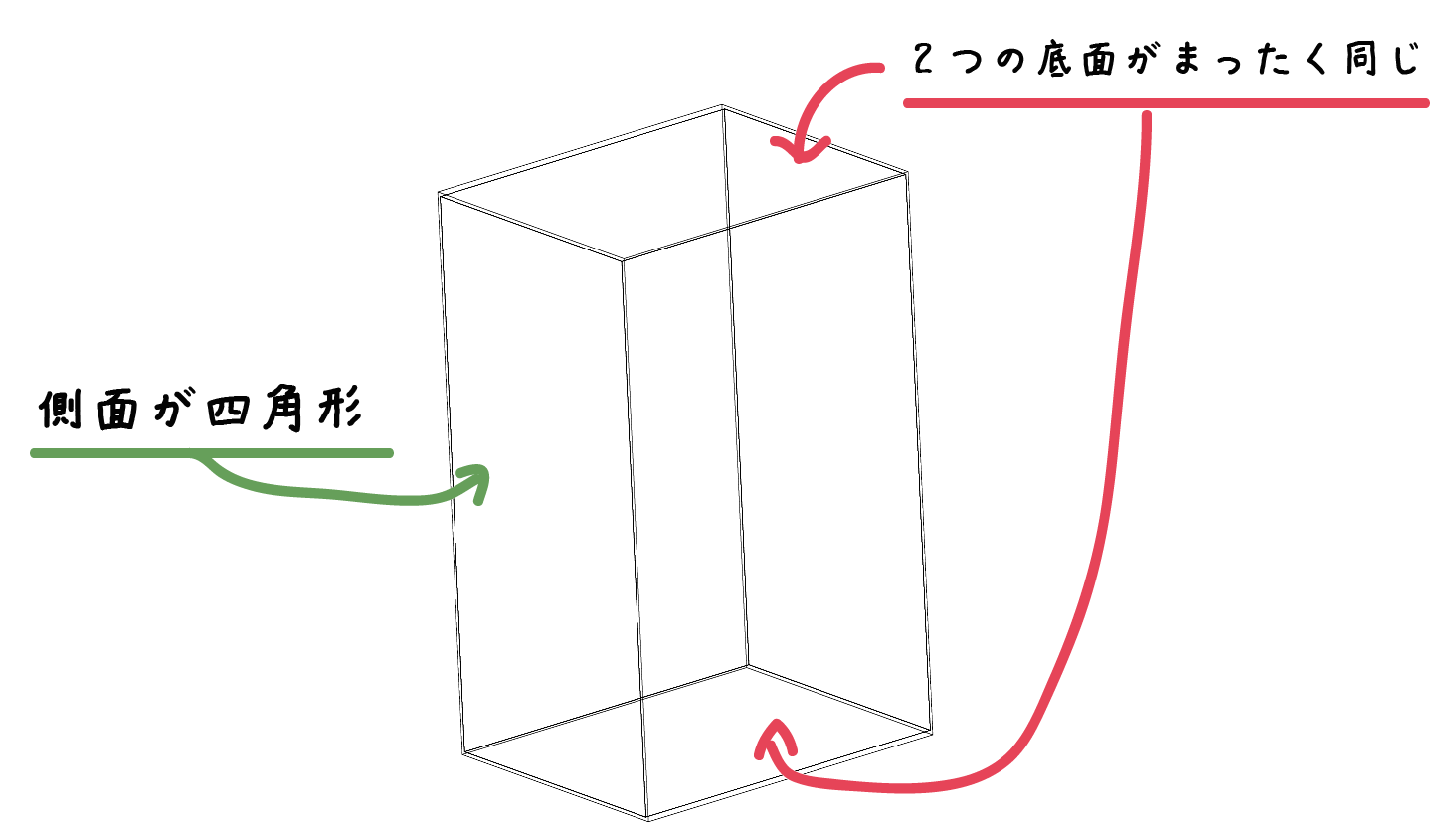
この種類の立体には、ゼッタイに、
柱(はしら)
っていう文字がついてる。
だけど、立体の名前では「チュウ」って読むから気をつけてね。
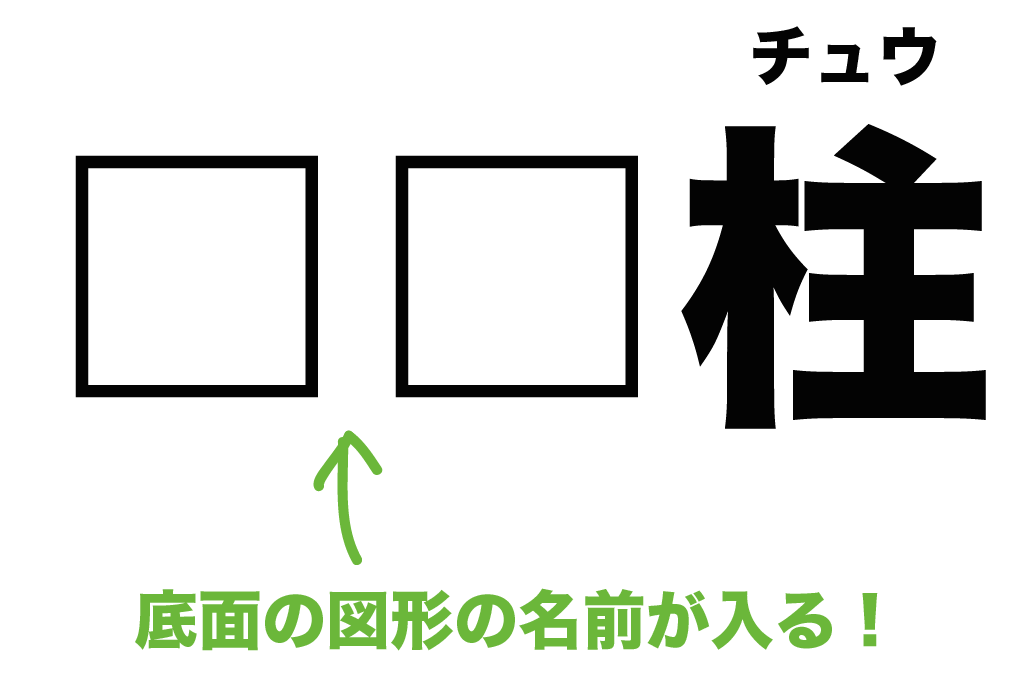
柱の前には「底面の図形」の名前が入るんだ。
底面の図形の種類によって、立体の名前が変わってくるってことだね。
そんで、「柱系の立体」には大きく分けてつぎの2つの種類の立体があるよ。
底面が多角形のもの
を「角柱」とよんでいるよ。
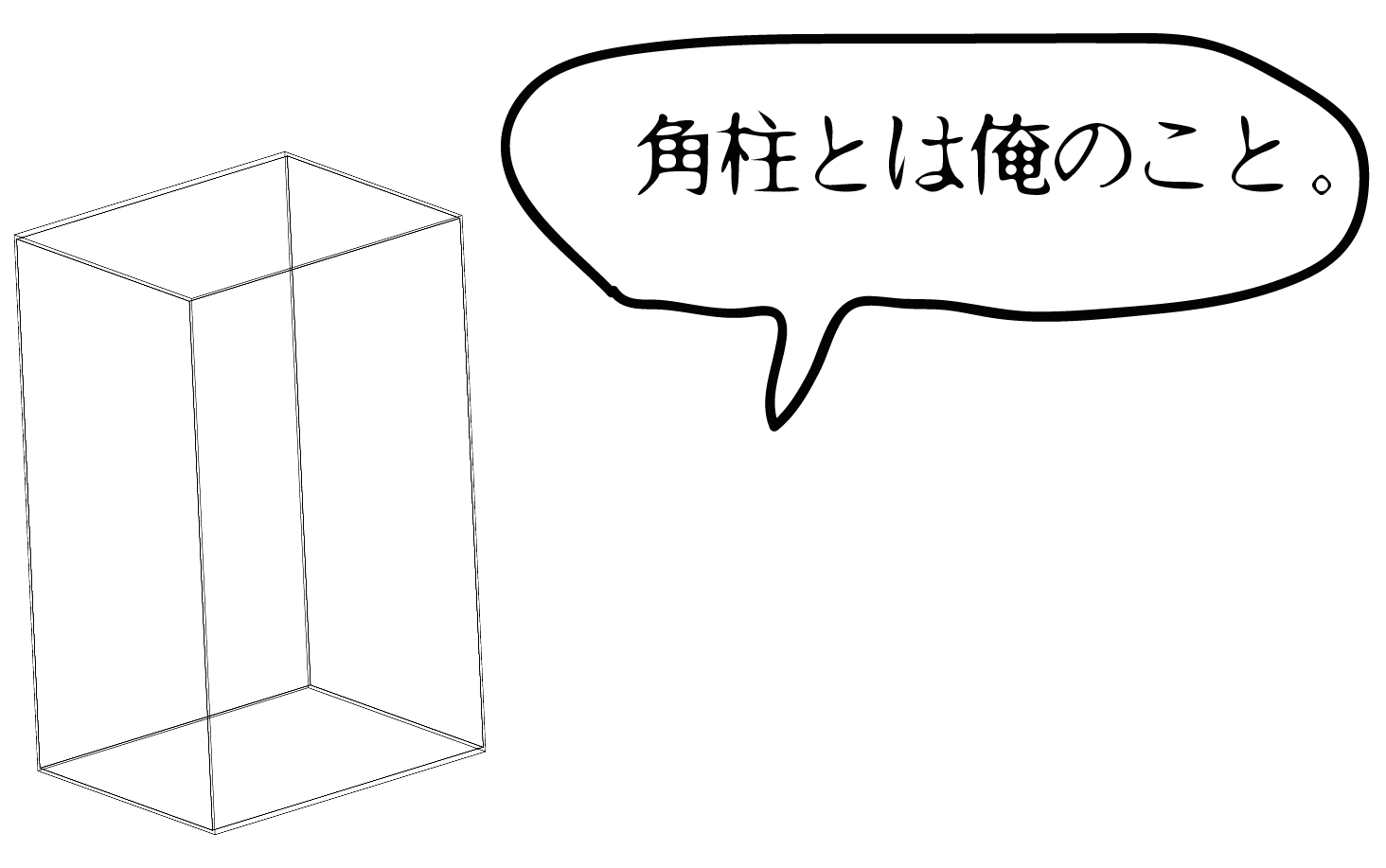
この「角柱」にもいろいろな種類のやつがいる。その角柱の名前は、
底面の多角形が「何角形になるか」で変わってくるんだ。
たとえば、
・・・・などなど。
そんで、もし、底面の辺の長さがすべて等しい場合、角柱の名前のまえに「正」がつくんだ。
たとえば、正三角形を底面とする角柱は、
「正三角柱」になるよ。
底面が「円」のときは「円柱(えんちゅう)」って呼ばれるんだ。

あれ?? 側面が四角形じゃなくない??
って思うかもしれないね。だけれど、こいつを切りひらいてやると、
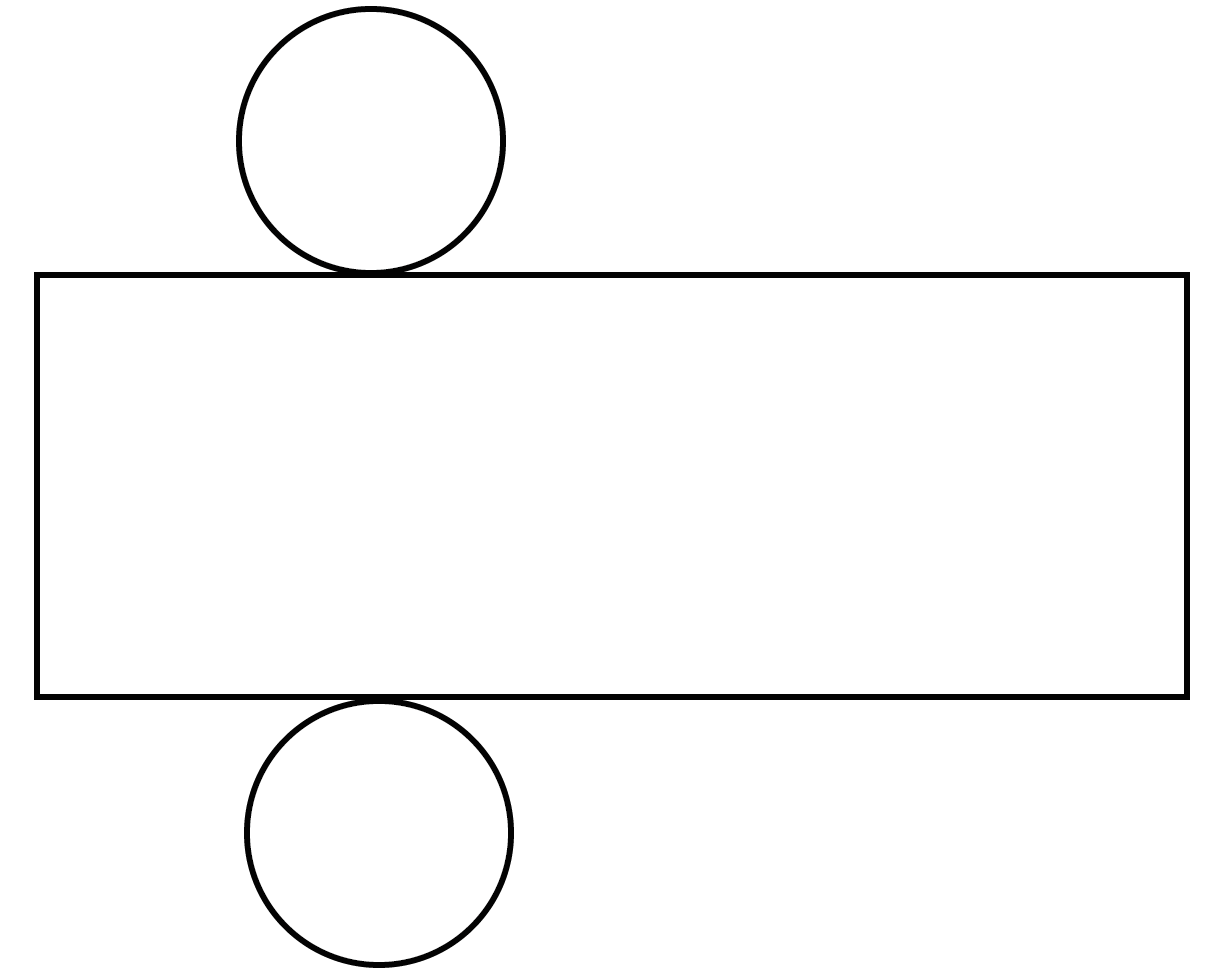
側面が長方形になっていることがわかる。
こいつはまぎれもない「柱系の空間図形」だ!
つづいては「錐系の立体図形」たちだ。
「錐(きり)」といえば、工具の一種。先端が尖っているアイツだね。

錐系の立体図形は、
底面が1つしかなく、底面の逆側は頂点の1点で交わっている立体
のことだ。
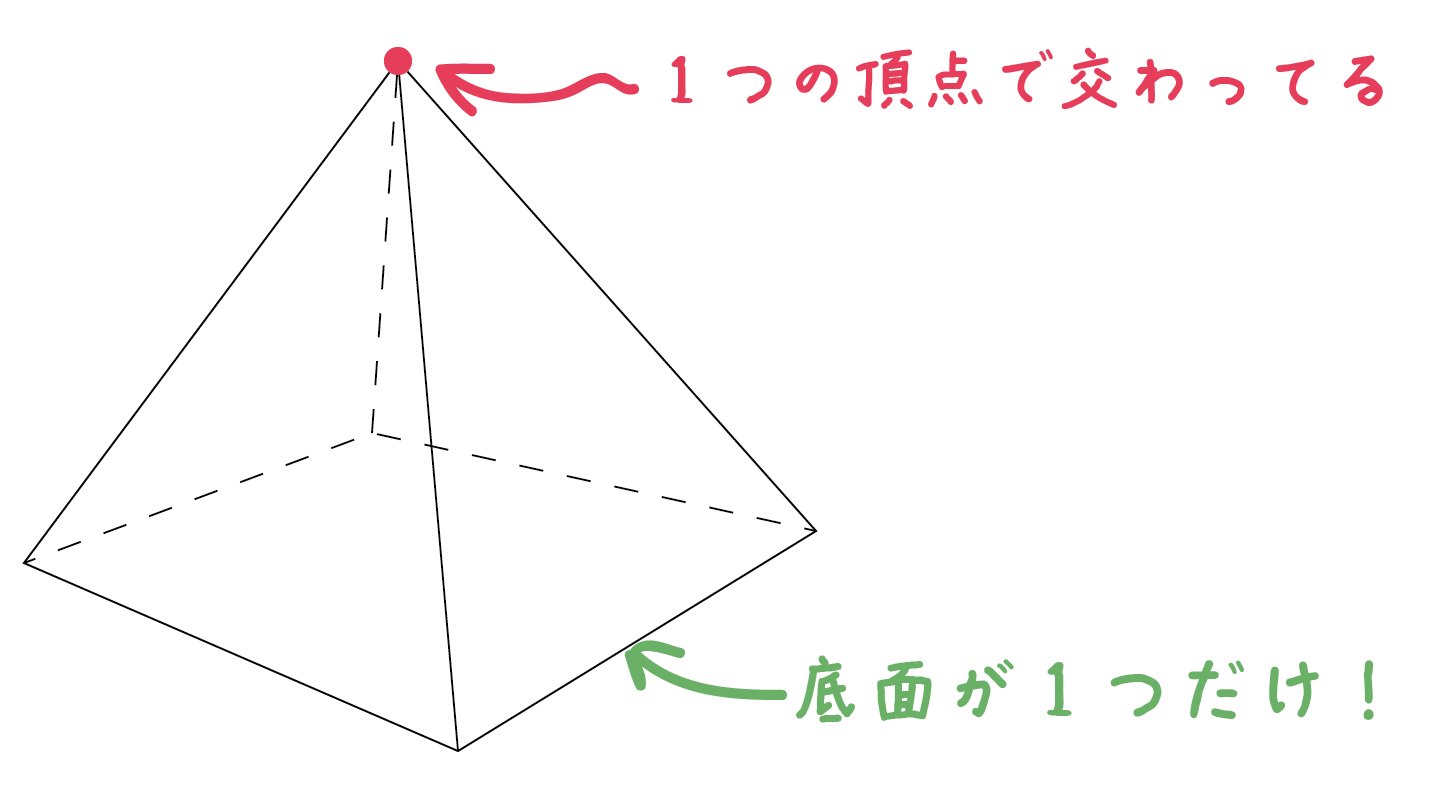
そして、「錐系の立体図形」の名前にはかならず「錐(すい)」が入ってるよ。
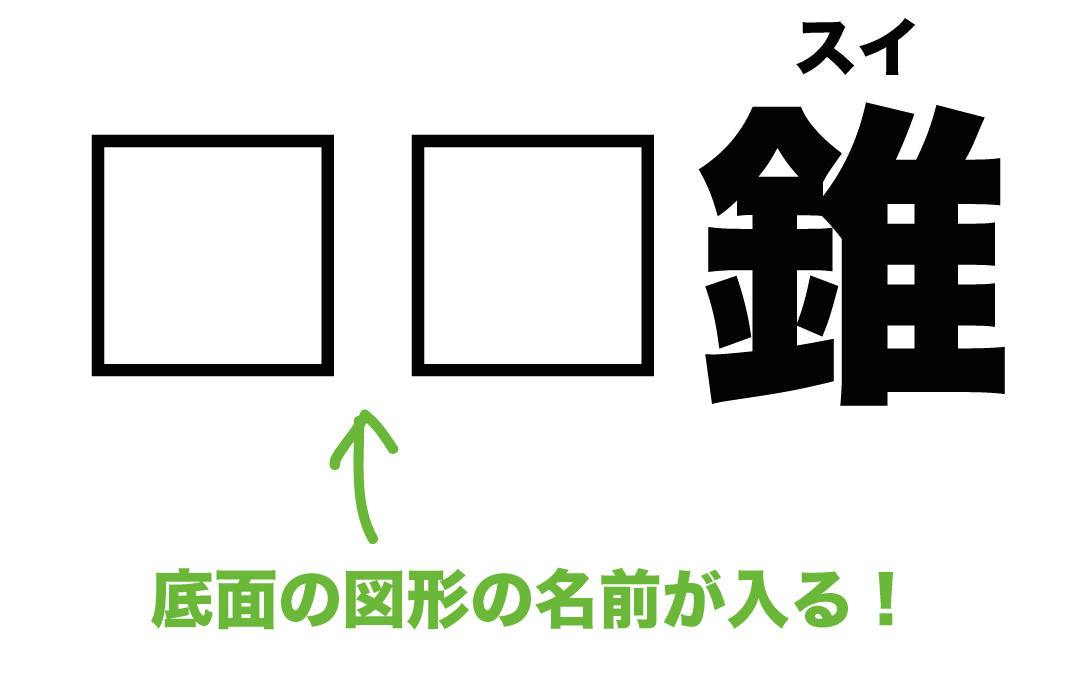
柱系の立体とおなじく、「錐」の前には「底面の図形の名前」をいれていくんだ。
これによって、立体の種類が変わってくるよー
それじゃあ、具体的な「立体の名前」をみていこう。
「底面が多角形になっている錐系の立体」を「角錐」っていうんだ。
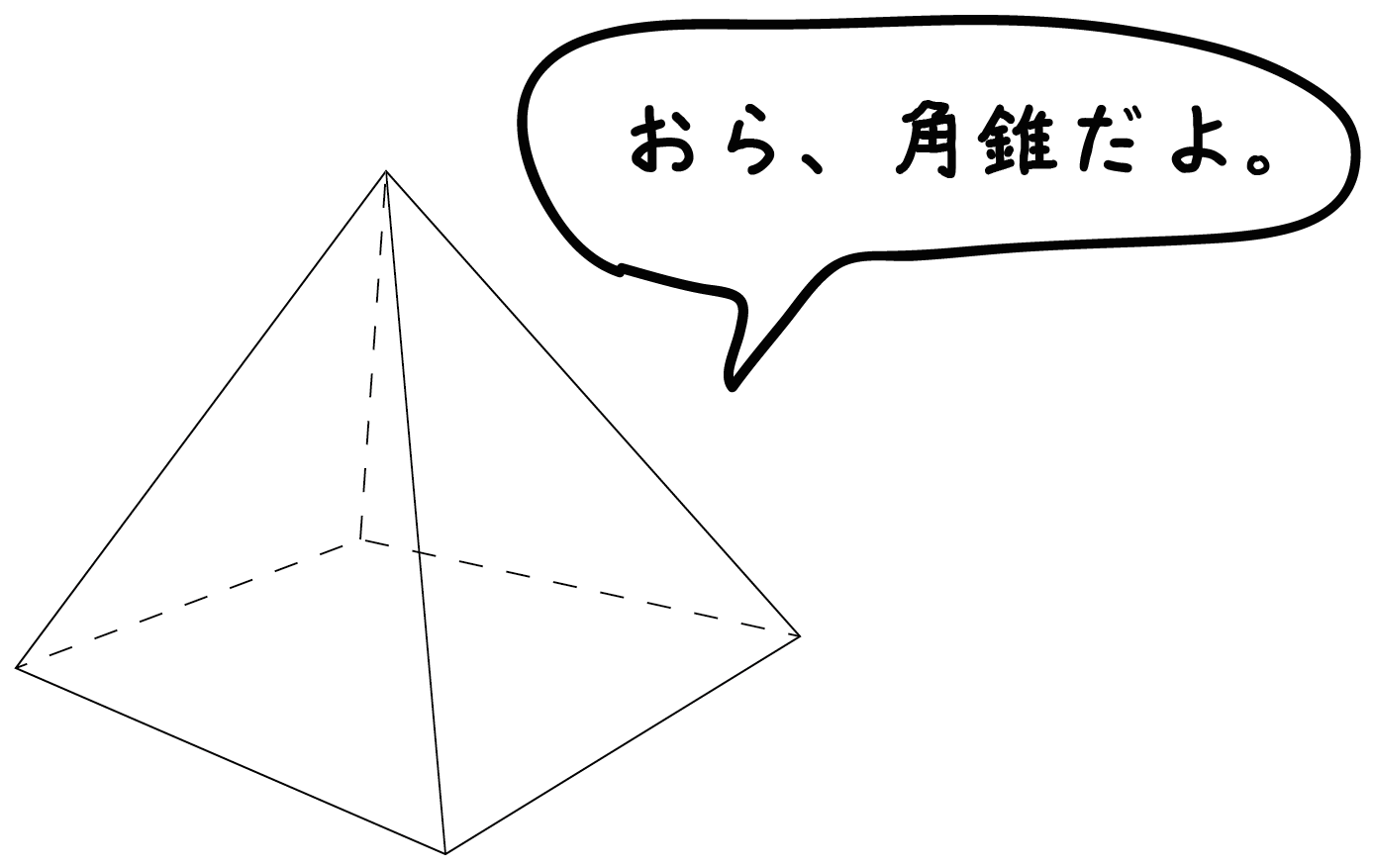
これは角柱と同じで、
といったように、底面の図形の名前が「錐」の前につくだけだよ。
それで、底面の辺の長さがすべて等しかったら、「正」という文字がつけられるんだ。
たとえば、「底面が正三角形の角錐」だったら「正三角錐」になるよー
円錐は「円」が底面になっている「錐系の立体」のことさ。

よく工事現場においてあるコーンなんかがそれにあたる。

この立体は表面積や体積をもとめる問題として狙われやすいよ。
十分に注意しておこう!
錐系の立体の「頂点」をスパッと切り落とした立体だ。
底面に平行にきってあげたあとに残る立体のことをさすんだ。これには、
の2種類がある。
角錐を底面に平行にスパッと切ったものを「角錐台」、円錐の場合は「円錐台」になるんだ。
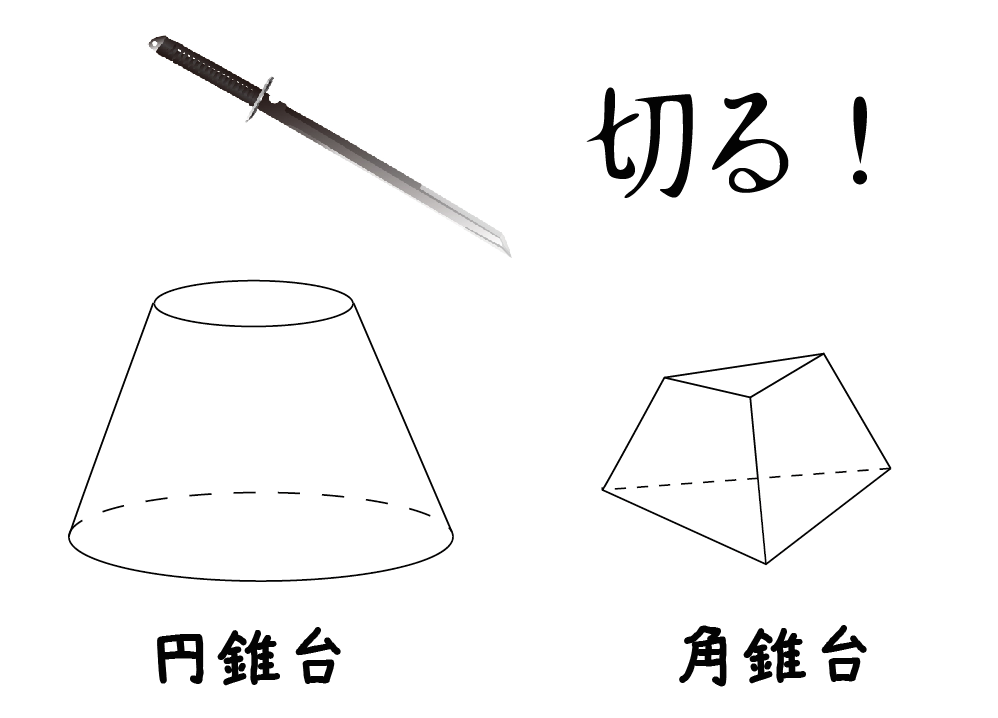
名前のうしろに「台」をつけるだけだね。
さて、最後の立体の種類「正多面体」の紹介だ。正多面体とはコトバンクによると、
各面がすべて合同な正多角形で、各頂点に同数の面が集まる多面体。
とあるね。
多面体とはすべて平面でできた立体のこと。その多面体をつくる「辺の長さがすべて等しい」ってわけだね。
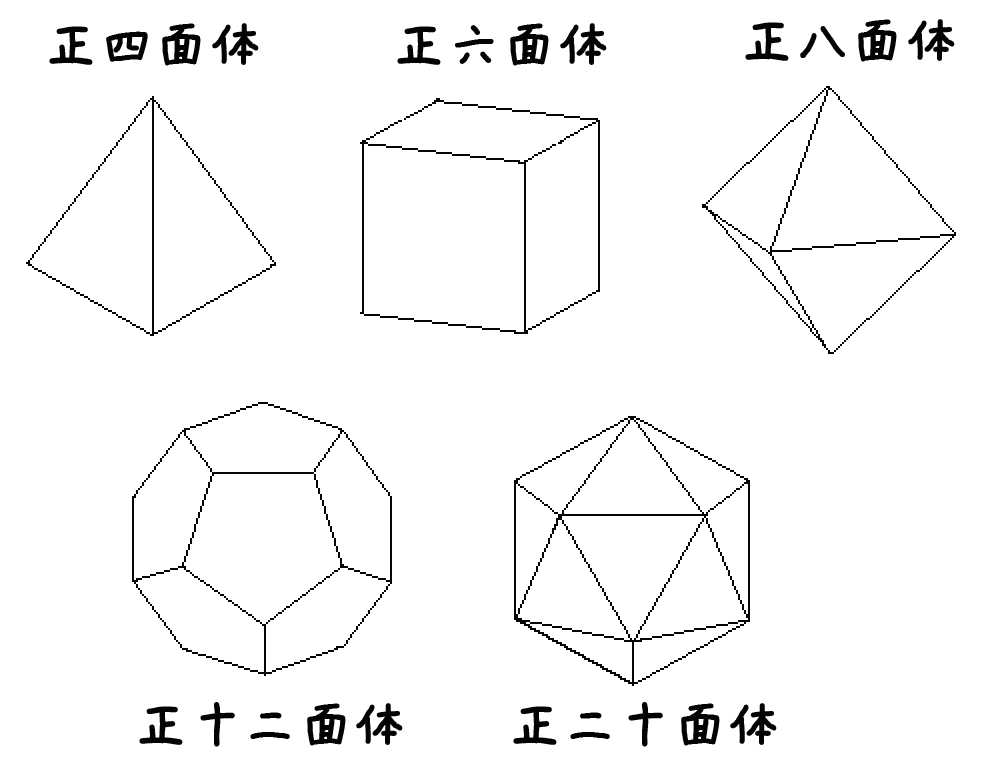
正多面体にはつぎの5種類しか存在していないんだ。
正多面体ネタはたまーにテストで狙われるよ。気をつけてっ!
ここまでみてきた立体の名前をぜんぶ覚えなくても大丈夫。
だいたいどんな立体の種類があったか、ってことをチラ見しておいてね。
さあ、これから空間図形を勉強していくよー!
そんじゃねー
Ken