星形の角度の求め方ってあるの？？
ある日、数学が苦手なかなちゃんは、
星がかけなくて困っていました。
だああー！
星かけねえええええ
おっ、苦戦してるね！
定規で一筆書きするといいよ。
へー！
やってみよっかなあー
わ！かけた！
でしょでしょ？？
じつはね、
数学の問題には、
星形の角度を求める問題
があるんだ。
たとえば、こんな感じ↓↓
つぎの星形の角度のxを求めなさい。
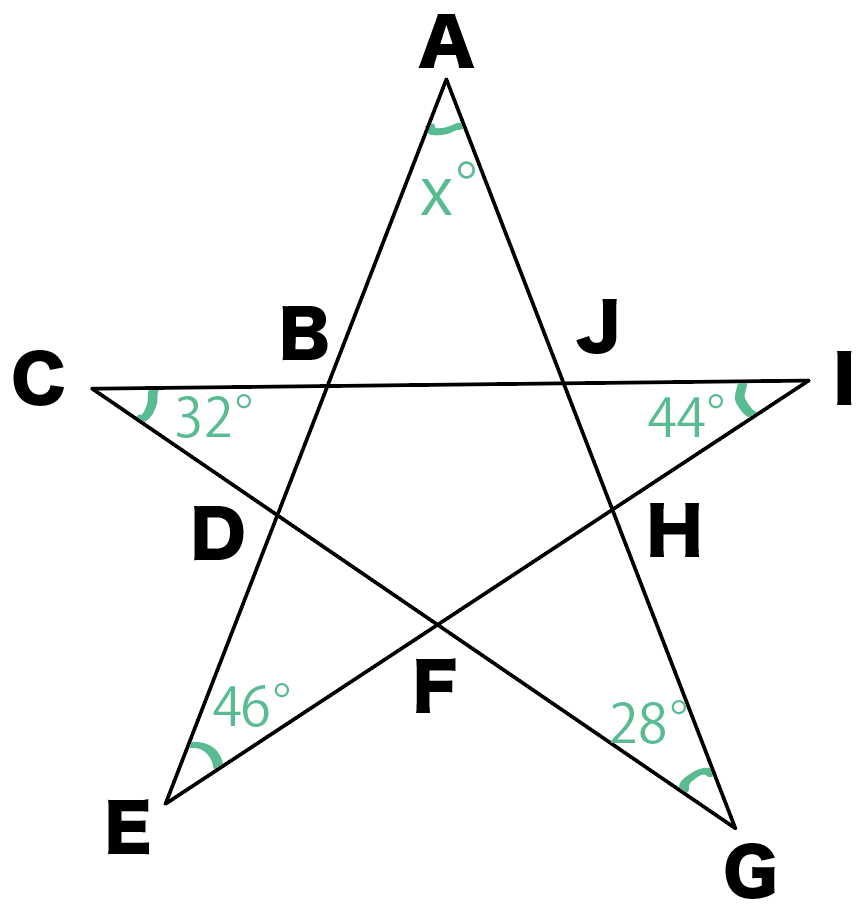
ひょえー！
雰囲気むずそーー
いや！
基本おさえちゃえば大丈夫。
いっしょにといていこう！
はい！！
星形の角度の求め方がわかる3ステップ
星形の角度の求め方はつぎの3ステップだよ。
- 三角形にわける
- 角を移動させる
- 三角形の内角に注目する
へー！
3ステップならできそう！
いけるいける！
それじゃあ、
さっきの星形の問題をといていこう。
つぎの星形の角度のxを求めなさい。
Step1. 「3つの三角形にわける」
星形を、
「3つの三角形」
にわけて考えてみよう。
えっと・・・・
3つ？？
そうそう。
星形の中に、
色んな図形が見えてこない？？
三角形と….
あっ、
五角形もある！！
そう！
今回は、その中の3つの三角形に注目しよう。
練習問題でいうと、
- △AEH
- △CGJ
- △HIJ
の3つだね。
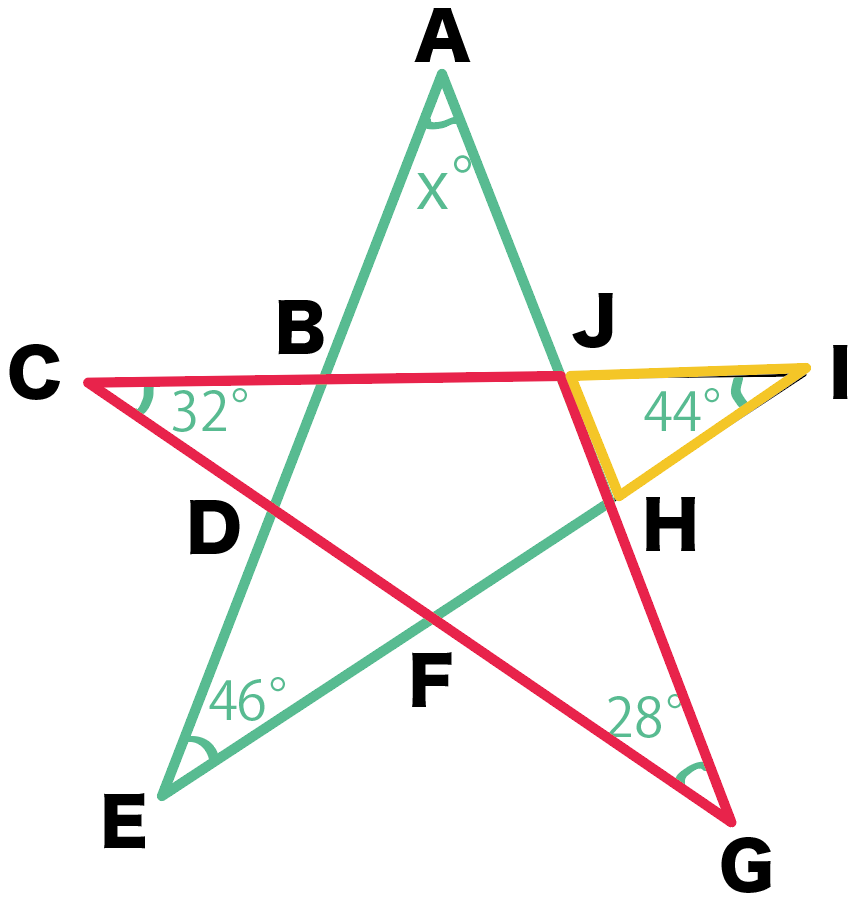
ひー
なんでその3つなんだろう？
それはね……
ひ、み、つ
Step2. 「三角形の外角の定理」をつかう
えっ！
外角の定理ってなんだっけ？？
っていう人もいると思って、
ちゃんと用意しといたよ！
さ、さすがすぎる！！
簡単にいうと、
三角形の内角を2つ足すと、
接してない外角になる
ってやつ。
下の図でいうと、
○と×をたしたら、
外角は「○+×」になるってわけ。
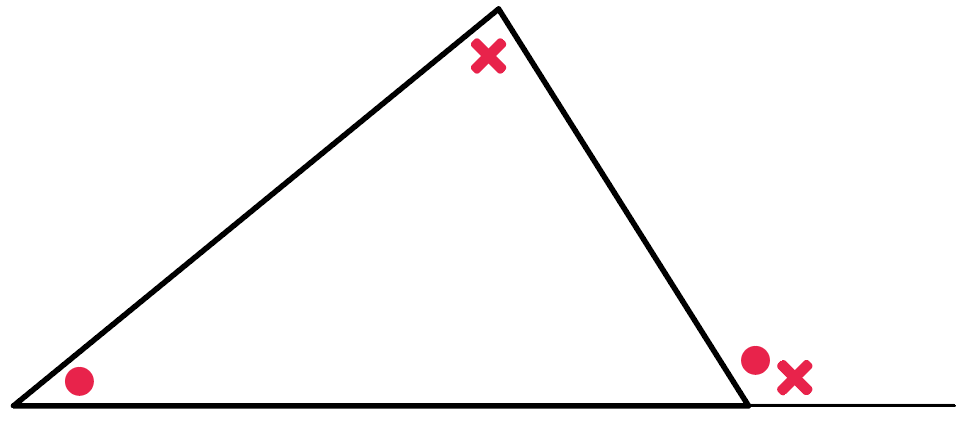
ああああああー
思い出してきたようなきがする！
これを星形の中の、
3つの三角形で考えてみよう！
外角になりそうなところ……
あっ、あった！
△AEHの外角は∠JHIだ！
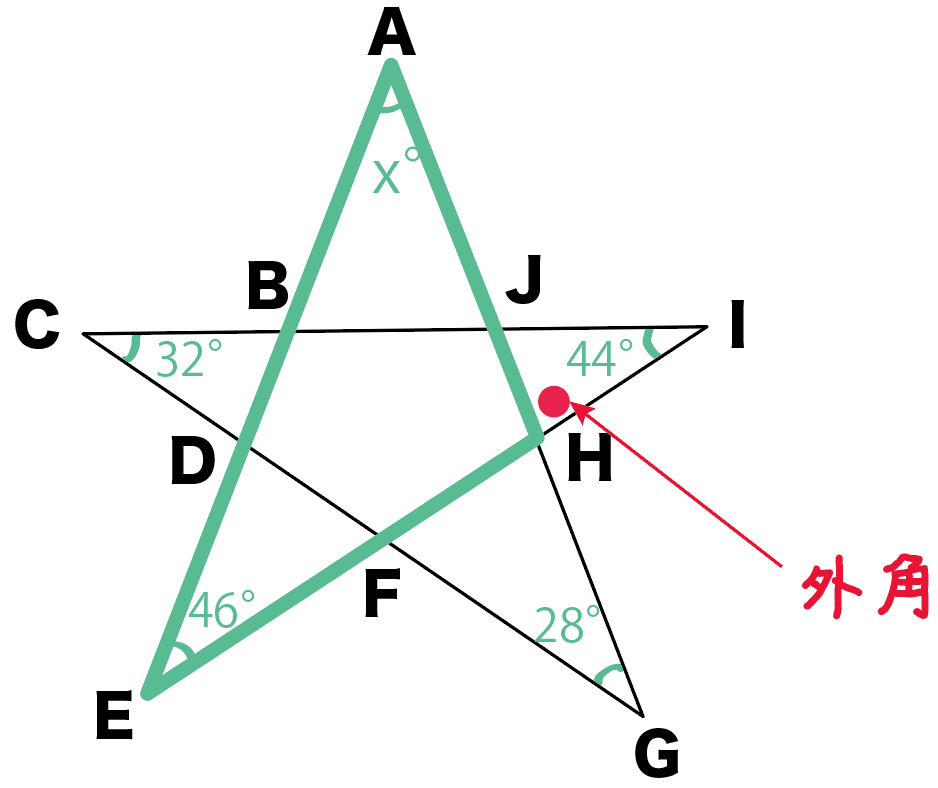
いいね。
△CGJでも同じように考えると……
あっ！
△CGJでいうと、∠HJIが外角になってる！
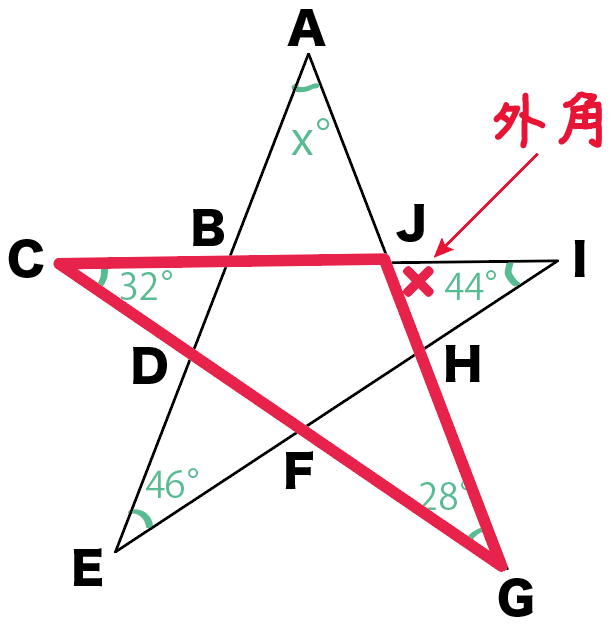
三角形の外角の定理で、
角を移動させるとどうなる？？
えっと・・・・、
あっ。
小さい三角形に集まってない！？？
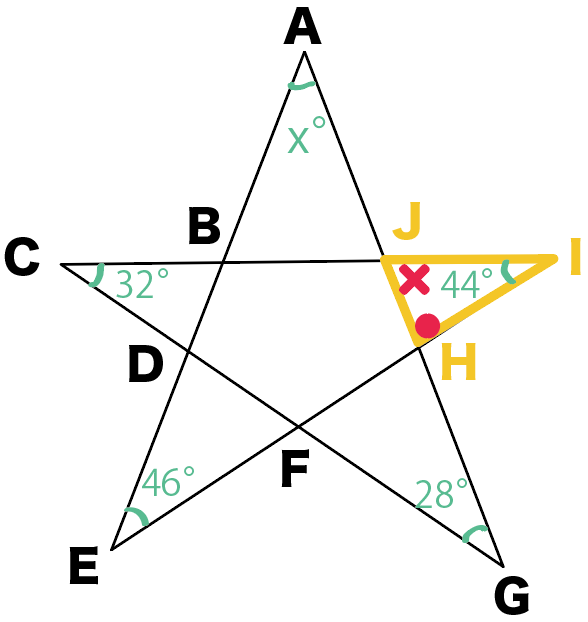
そう！
ぜんぶあわせて三角形の内角になってるね。
ということは？？
三角形の内角の和は180度だから、
星の角度の和が180度になるってことだ！！
いいね！
じゃあ、角xはいくつ？？
えっと・・・、
三角形の外角の定理をつかうと、
- ∠JHI = 46 + x
- ∠HJI = 32 + 28 = 60
になる。
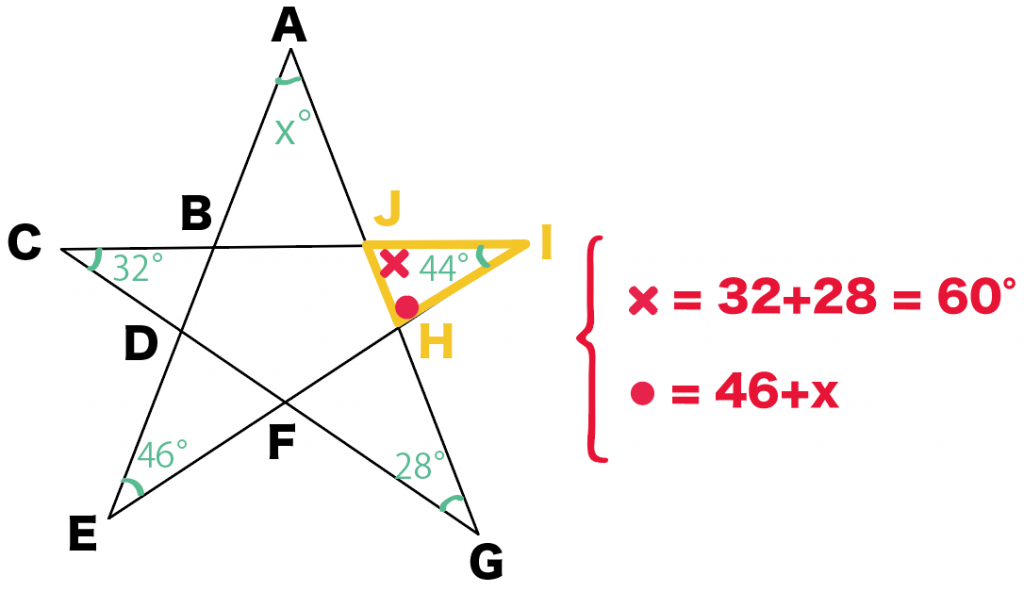
うんうん
だから、△HIJの内角は全部で180度だから、
(46+x) + 60 + 44 = 180
x = 30°
だ！
xは30°！
まとめ：星形の角度をぜんぶたしたら180°！
星形の角度の求め方はどうだったかな？
- 三角形にわける
- 外角の定理をつかう
- 小さな三角形の内角に注目
の3ステップだったね。
これなら、
他の問題も解けそうかも！！
いいね、このことを利用した問題は、
まだまだたくさんあるんだ。
最初はよく分かんなかったけど、
特徴さえわかっちゃえば、分かりやすいね！！
そう！
どんな問題でも、
初めては分かりづらい。
けど、一度理解すれば大丈夫。
色んな問題が解けるようになるよ！
はい！
ありがとうございました！
