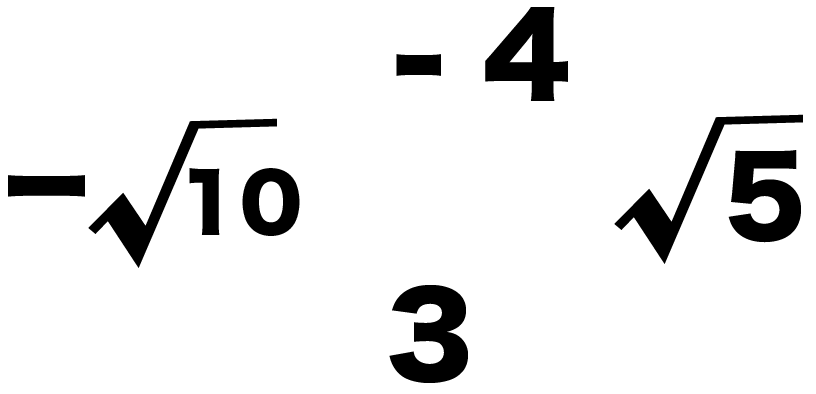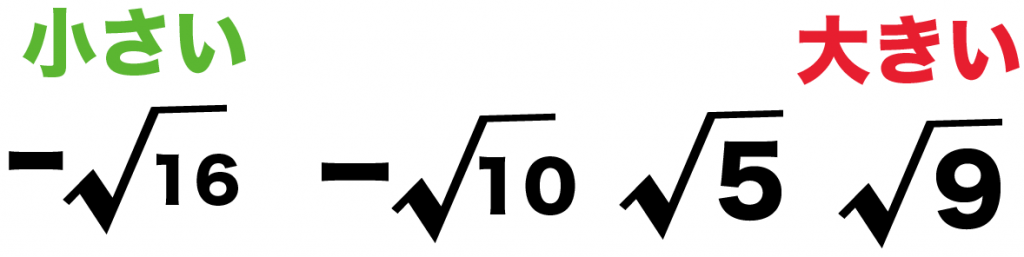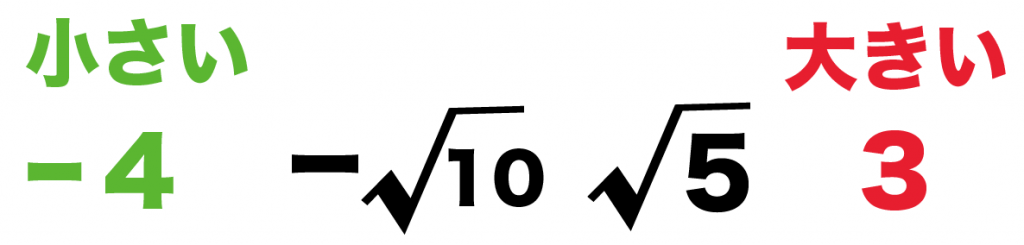【中3数学】平方根(ルート)の大小問題の2つの解き方
平方根(ルート)の大小の問題を解きたい!!
こんにちは!この記事をかいてるKenです。レモンは皮がうまいね。
ルートの問題でよくでてくるのは、
平方根の大小
の問題だ。
ようは、
整数や平方根をみくらべて、どっちのほうがデカいのか??
をあてる問題だ。
はじめてだと大小をくらべるのはムズいよね。
わかるよ、その気持ち。
平方根の大小ででてくる2つの問題
でもじつは、
平方根の大小の問題はシンプルなんだ。
なぜなら、問題の種類をたった2タイプにわけられるからね。
- 平方根同士の大小をくらべる問題
- 平方根と整数の大小をくらべる問題
この2つさえマスターすればこっちのもの。
今日は、この2つの問題をくわしくみていこう!!
平方根同士の大小をくらべる問題
まずは、
平方根と平方根の大小をくらべる問題
だ。
たとえば、つぎのような問題だね↓↓
例題
つぎの2つの平方根の大小を不等号をつかってあらわしなさい。
- ルート2
- ルート6

解き方はちょー簡単。
ルートをとっぱらって大小をくらべればいい
のさ。
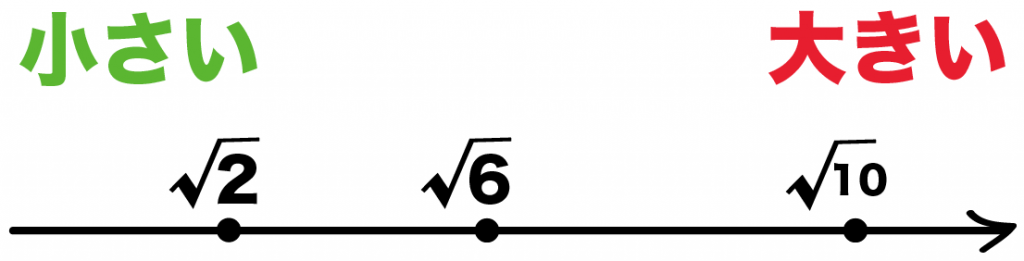
さっきの例題をみてみて。
- √2
- √6
をくらべるのはむずいね??
だから、思い切って√をとって、中身の、
- 2
- 6
の大小をくらべるんだ。
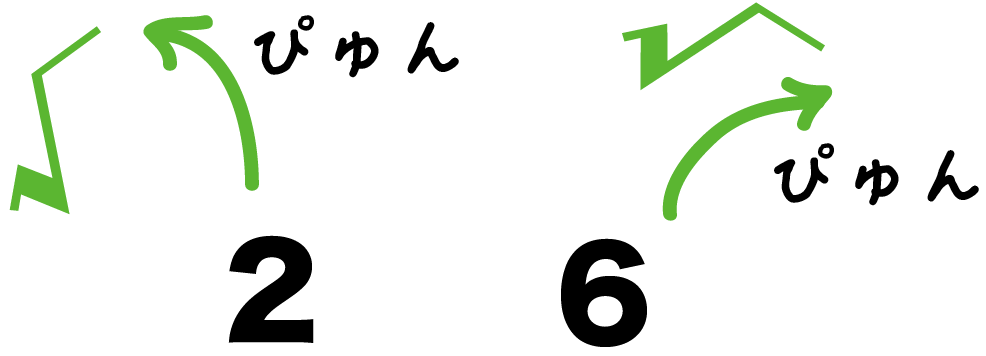
2と6をくらべると、
あきらかに6が大きいよね??
だから、√をつけても√6のほうが大きいのさ。
えっ。なぜこんなことがまかり通るのかって!??
じつは、平方根には、
√の中身が大きいほど絶対値が大きくなる
っていう性質があるからなんだ。
だから、√2よりも√6が大きいし、
√10なんてもっと大きい。
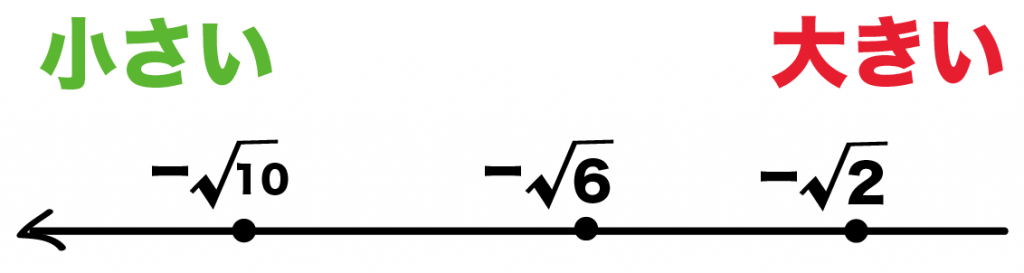
逆に負の平方根でいうと、
-√2より-√6のほうが小さいし、-√10なんてもっと小さい。
なぜなら、
負の数では絶対値が大きいほど小さくなるからね。
こんな感じで、平方根同士の大小をくらべるときは、
√の中身と符号で判断しよう!
「整数」と「平方根の大小」をくらべる問題
つぎは「整数」と「平方根」をくらべる問題。
たとえば、つぎみたいなヤツだね ↓↓
例題
つぎの4つの数字の大小を不等号をつかってあらわしなさい。
- -√10
- 3
- √5
- -4
このタイプの問題は、さっきよりもヤッカイ。
なぜなら、
整数を平方根になおす
必要があるからね。
整数と平方根同士をくらべるのはむずい。
だから、
整数を平方根にしてやって、
平方根同士をくらべる路線にもっていくんだ。
例題で整数なのは、
- -4
- 3
の2つ。
こいつらを平方根であらわしてみよう!
えっ。平方根になおす方法がわからないだって?!?
やり方は簡単。
あえて2乗してルートのなかにぶちこめばいいんだ。
だから、
- -4
- 3
はそれぞれ、
- -√16
- √9
の平方根に置き換えられるわけさ。
こんな感じで、ぜーんぶ平方根になおせば一件落着。
さっきの「平方根同士の大小の解き方」でとけちゃうよね。
小さい順にならべてみると、
-√16, -√10, √5, √9
になるね。
んで、
さっき平方根にした整数をもとにもどすと、
-4, -√10, √5, 3
になるはずだ!
ついでに不等号であらわすと、
-4 < -√10 < √5 < 3
になるね。
おめでとう!
どんな大小でもバッチコイだ!
まとめ: 平方根の大小の問題は2種類!
平方根の大小の問題??
やばそうにきこえるけど、意外に簡単。
- 平方根同士でくらべる問題
- 平方根と整数をくらべる問題
の2種類しかないからね。
平方根同士だったらルートを無視。
整数は平方根になおしてみよう。
そんじゃねー
Ken