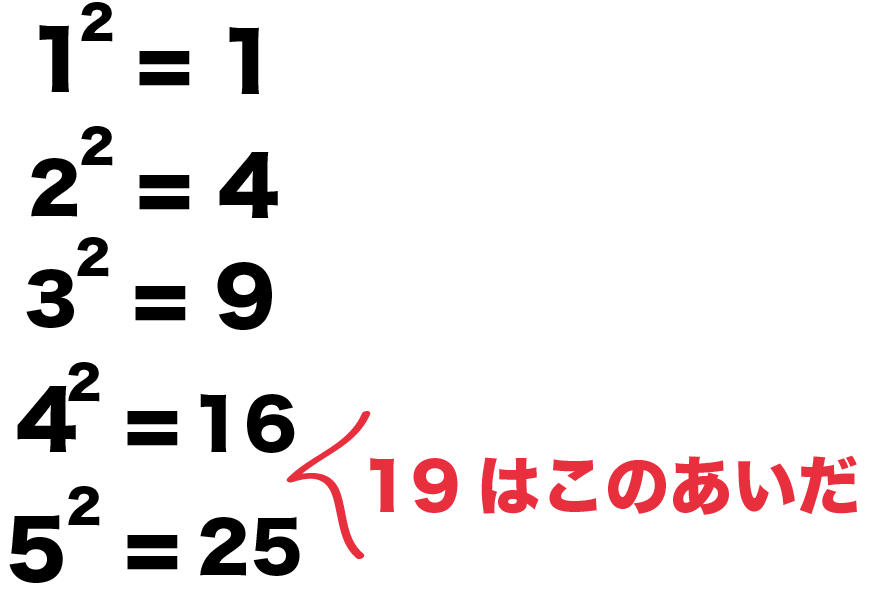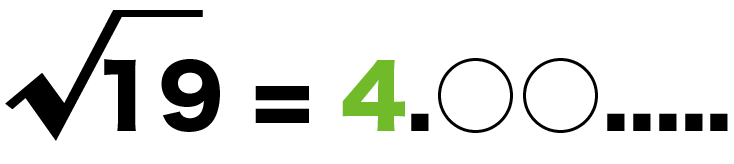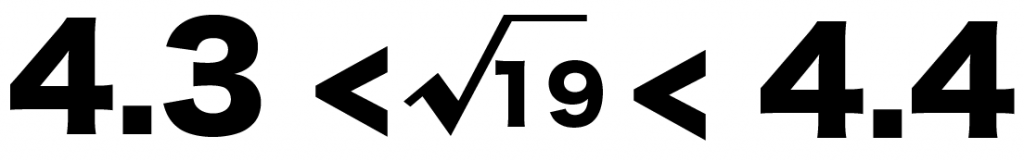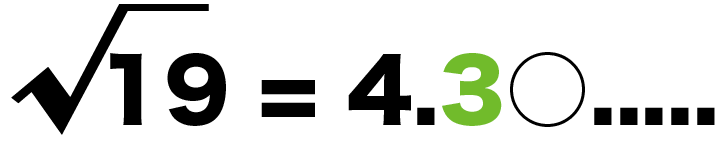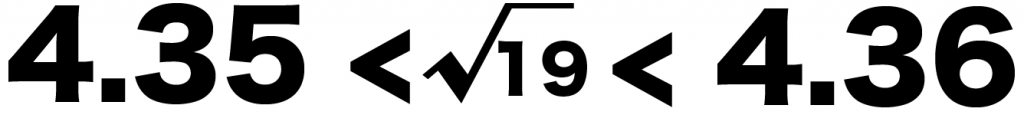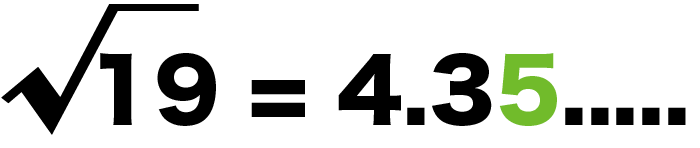【中学数学】3分でわかる!平方根の近似値の求め方
平方根の近似値の求め方を知りたい!
こんにちは!この記事をかいているKenだよ。血糖値は高いね。
平方根をみていると、
どれくらいの大きさなんだろうな・・?
って思うことあるよね。
ルート!ルート!
っていわれてもデカさわからんし。
たとえば、ある少年に、
19万円ほしい
っていわれたら、大きい金額であるし、慎重になるじゃん??
でもさ、
ルート19万円ほしい
っていわれてもピンとこないよね??。
高いのか低いのか検討もつかん。
今日はそんな事態に備えて、
平方根のだいたいの値の求め方を勉強していこう。
この「だいたいの値」のことを、
数学では「近似値」とよんでいるんだ。
3分でわかる!平方根の近似値の求め方
平方根の近似値を求め方では、
大きな数であてをつけて、じょじょに範囲をせばめていく
っていう手法をつかうよ。
だから、まずは、
その平方根がどの整数の範囲におさまっているのか??
を調べる必要があるんだ。
さっきでてきた、
√19万円
がだいたい何万円になっているのか??
を調べていこう!
Step1. 整数で近似値のあてをつける
まずは、
平方根がどの整数と整数の間にあるのか??
のあてをつけよう。
あての付け方としては、
2乗をしたときに√の中身をこえてしまう整数
と
ギリギリこえない整数
をだせばいいんだ。
√19で考えてみよう。
整数を1から順番に2乗してみると、
- 1の2乗 = 1
- 2の2乗 = 4
- 3の2乗 = 9
- 4の2乗 = 16
- 5の2乗 = 25
・・・・・・・
になるね。
どうやら、「19」は、
- 4の2乗 = 16
- 5の2乗 = 25
のあいだにありそうだね。
よって、√19は、
4 < √19 < 5
の範囲におさまってるはず!
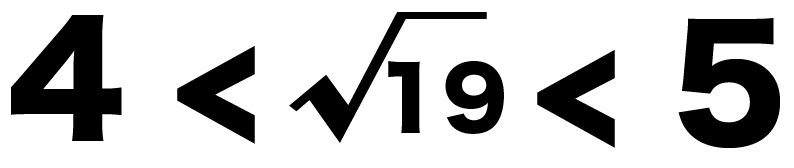
つまり、
√19の1の位は「4」ってわけだね。
ふう!
Step2. 小数第1位をもとめる
近似値の1の位はわかったね??
おなじことを小数第1位でもやろう。
「√19」の1の位は4だったね??
今度は、小数第一位の数字を1から順番に大きくしていこう。
んで、
2乗して19をこえるポイントをみつければいいんだ。
- 4.1の2乗 = 16.81
- 4.2の2乗 = 17.64
- 4. 3の2乗 = 18.94
- 4.4の2乗 = 19.36
・・・・
ぬぬ!
19は、どうやら、
- 4.3の2乗
- 4.4の2乗
のあいだにありそうだね。

ってことは、√19の範囲は、
4.3 < √19 < 4.4
になるはずだ。
だから、√19の小数第1位は「3」になるはずだね。
Step3. 小数第2位をもとめる
最後もやり方はおなじ。
小数第2位を1から順番に増やして2乗。
ルートの中身を超えるポイントをみつければいいんだ。
√19でも小数第2位のあてをつけよう!
小数第1位は「3」だったよね??
だから、調べるのは4.31からだ。
0.01ずつたして、そいつらを2乗していこう!
- 4.31の2乗 = 18.5761
- 4.32の2乗 = 18.6624
- 4. 33の2乗 = 18.7489
- 4.34の2乗 = 18.8356
- 4.35の2乗 = 18.9225
- 4.36の2乗 = 19.0096
おっと!
4.36の2乗で19をこえちゃったね。
ってことは、19は、
- 4.35の2乗
- 4.36の2乗
の間にあるはずなんだ。
つまり、
4.35 <√19 < 4.36
になってるね!
ってことは、
√19の小数第2位は「5」になるはず!
やったね!
この「4.35」が√19の小数第2位の近似値だよ。
あの少年は4.35万円、つまり、4万3500円ぐらいを請求していただわけだね。
まったく、可愛いけど憎いやつだ。
こんな感じで、
1の位からじょじょに範囲をせばめていこう!
平方根の近似値があってるか確認!
平方根の近似値があってるか確認してみて。
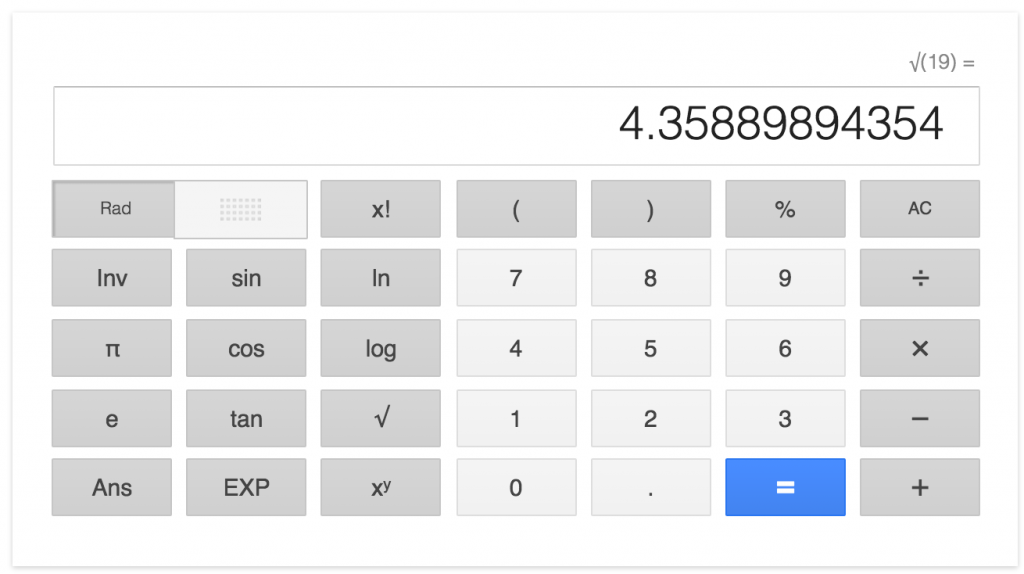
計算機の√ボタンをおしてやれば・・・・ほら!
一発で平方根の近似値がだせるんだ。
たくさんのケタ数をね。
うん!
たしかにあってる!
√19の小数第2位は「5」だもんね。
計算機で確認できるから便利だ。
まとめ:平方根の近似値の求め方は粘り強さでかとう!
平方根の近似値の求め方はシンプル。
1の位からじょじょに範囲をせばめればいいんだ。
池の魚をおいつめるみたいだね。
計算は大変だけど、気合と根性でせばめていこう!
そんじゃねー
Ken