覚えて損はない!相似な立体同士の3つの性質
相似な立体同士にはどういう性質がある?
やあ、がんばってるかい? Dr.リードだよっ。
相似の勉強もそろそろ終盤戦だ。
年間スケジュール達成のため、学校でもさらーっと流すことが多い。
そのペースに流されることなく、じっくり取り組んでほしいぞ。
今日のトピックは、
相似な立体同士にみられる性質
だ。
覚えて損はない!相似な立体同士の3つの性質
さっそく、相似な立体同士の性質を3つ紹介していくよ。
- 相似な立体同士は対応する線分の長さの比がすべて等しい
- 相似な立体同士の表面積比は相似比の2乗である
- 相似な立体同士の体積比は相似比の3乗である
性質1. 「線分の長さの比はすべて等しい」
まず1つ目の性質は、
相似な立体同士の線分の長さの比は等しい
ってヤツだ。
立体じゃなくて、平面図形の相似の性質があったよね?
それと同じさ。
たとえば、りんごジュースを買いにいったとしよう。
リードのジュースは君のより3倍でかい。
重いぞ。
飲みごたえたっぷりだ。
お得な3倍サイズって書いてあったんだよ。
ってことは、
- 君のりんごジュース
- リードの特大りんごジュース
は拡大縮小の関係になってるから、相似だよな。
で、対応する縦、横、高さの比を比べてみる。
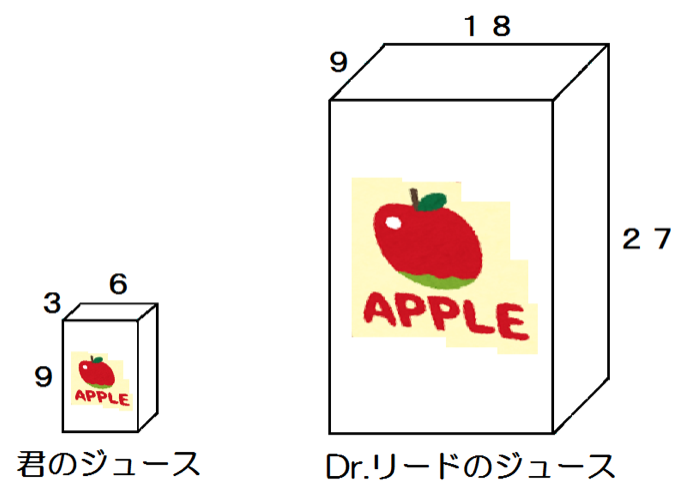
- 【君のジュース】 3 cm : 6 cm : 9 cm = 1 : 2 : 3
- 【Dr. リードのジュース】9 cm : 18 cm : 27 cm = 1 : 2 : 3
まっ、当たり前だけど、平面図形と同じで、対応する辺の比は同じだったぞ。
どの辺の長さも3倍になってるね!
こんな感じで、
相似な立体同士は各辺の相似比が一緒なんだ。
性質2. 「表面積の比は相似比の2乗となる」
次の相似な立体の性質は、
表面積の比は相似比の2乗になる
ってヤツだ。
たとえば、次の立方体が2つあったとしよう。
- 1辺の長さ : 1 cm
- 1辺の長さ : 2 cm
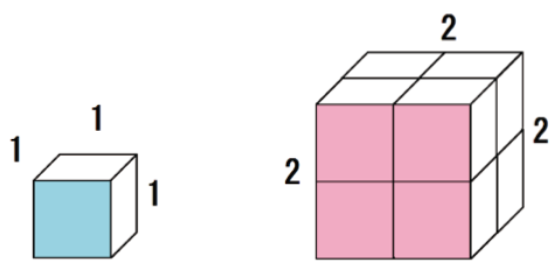
立体の相似比は1:2だから、表面積比はその2乗で、
1 : 4
になるってわけ。
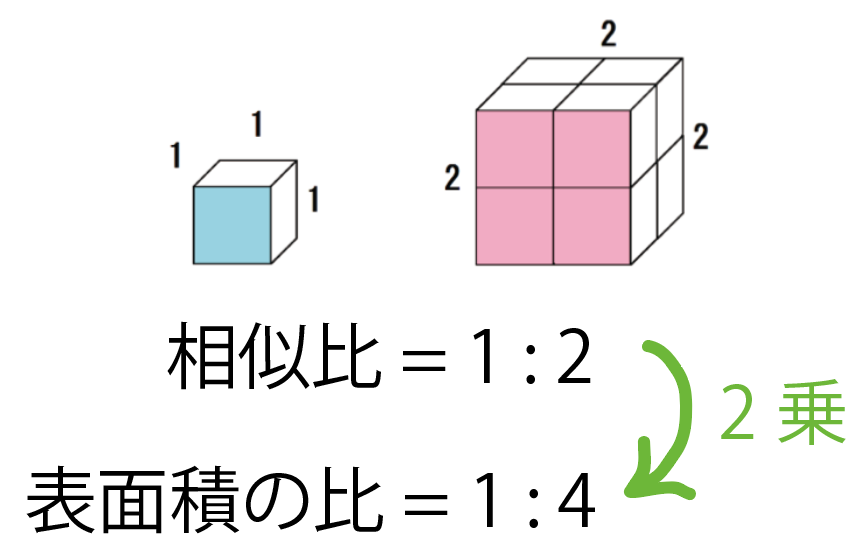
本当かどうか確かめよう。
表面積だから、展開図も書いてたしかめてみるな。
1×1×1の立方体の1つの面の面積は1 cm²。
よって、表面積は、
1×6 =6 cm²
だ。
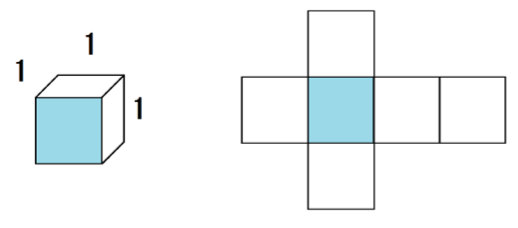
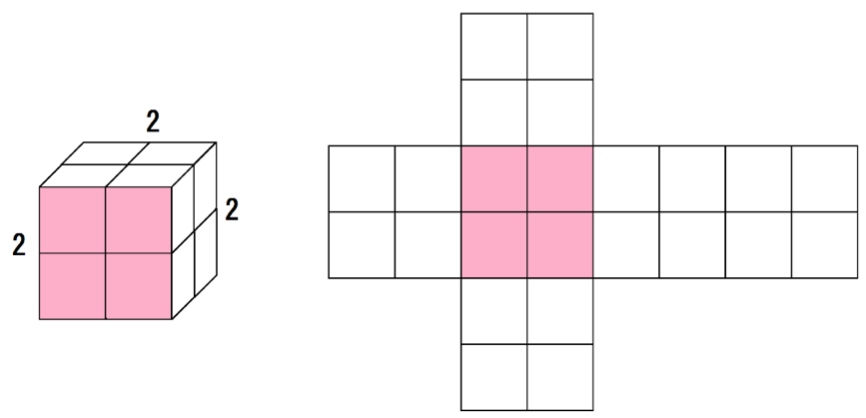
一方、相似比2倍の立方体はどうだろう??
立方体の1つの面の面積は4 cm²。
よって、表面積は、
4×6 = 24 cm²
になるね。
よって、表面積の比は、
6: 24 = 1 : 4 = 1² : 2²
相似な立体同士の表面積の比は、相似比1:2の2乗になってるね。
えっ。
相似比が1:3の場合でも表面積の比は1:3なのかって?!
疑い深いならたしかめてみようか。
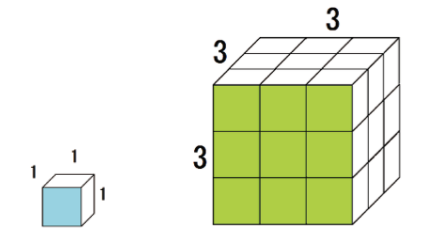
立方体の各辺が3倍になるとだな、
2つの立体の相似比は、
1 : 3
になるね?
1つの面の面積は、
3×3 = 9 cm²
よって、表面積は、
9×6 = 54 cm²
1辺の長さが1cmの立方体との表面積の比は、
6 : 54
= 1: 9 = 1² : 3²
になるね。
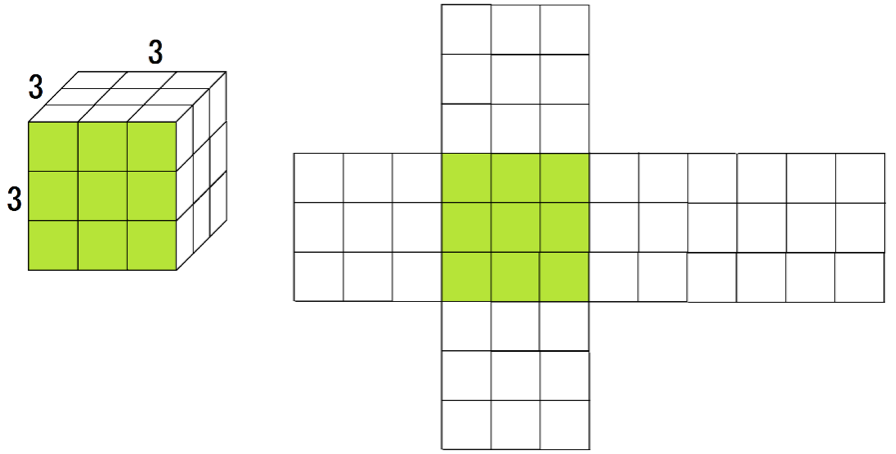
ねっ、今回も相似比の2乗になったぞ。
しかし、永遠に何倍何倍って確かめるわけにもいかんわな。
何倍かわからんがとりあえず、
「k倍」ってことにしてみるぞ。

1辺の長さが、
- a cm
- b cm
- c cm
の直方体で考えてみよう。
これをk倍してみると、
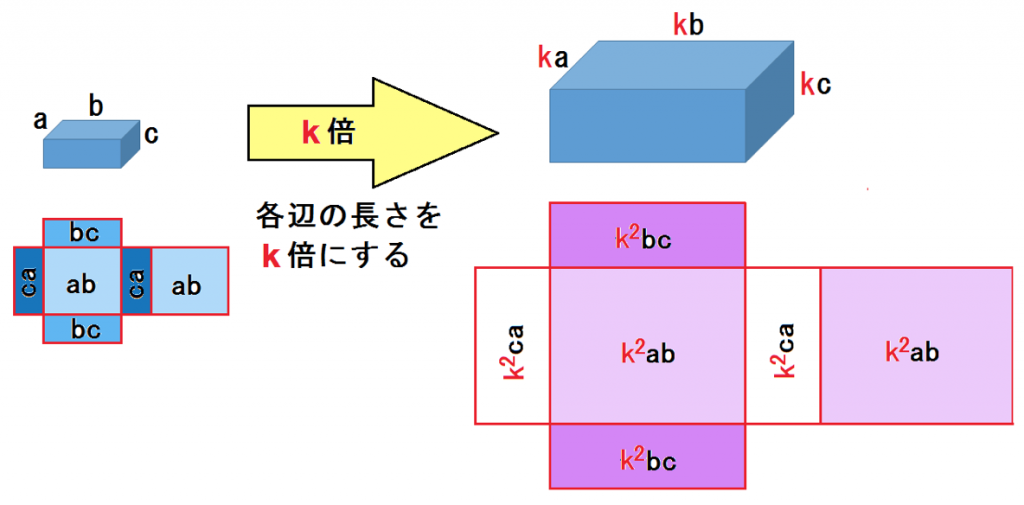
じゃーん!!!
やっぱり相似比の2乗になったね。
ってことで、相似な立体同士の表面積の比は相似比の2乗になってるんだ。
性質3. 「体積比は相似比の3乗」
最後の性質は、
相似な立体同士の相似比と体積比の関係だ。
おっ、なんかもうわかってる感じだな。
そう。
体積比は相似比の3乗になるんだ。
たとえば、さっきの3つの立方体をみてみよう。
相似比が1:2の立方体の体積比なら、
1³: 2³ = 1 : 8
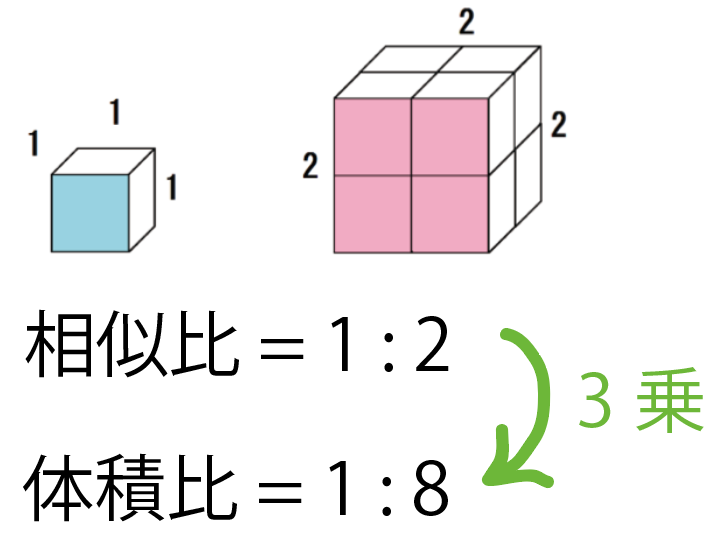
相似比が1:3の立方体なら、
体積比 = 1³ : 3³ = 1 : 27
になるってわけ!
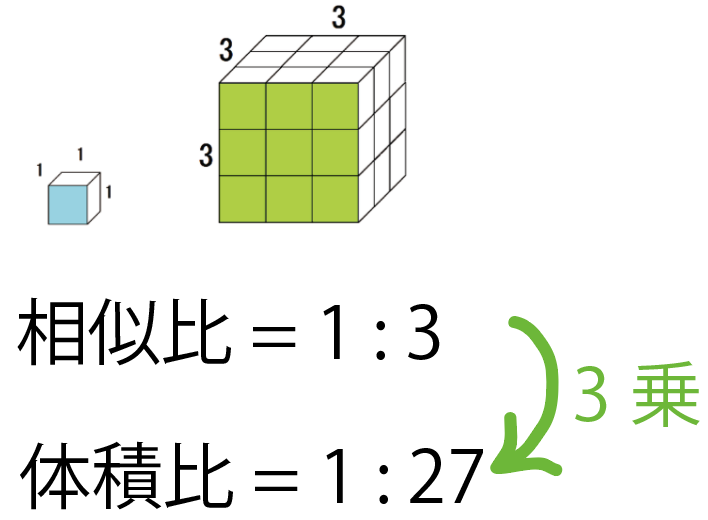
念のため、k倍のも確認すると、
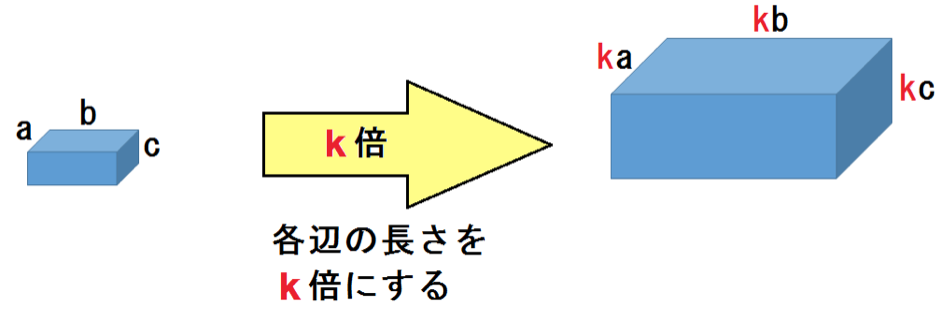
体積比
= abc : k³abc = 1 : k³
になるね。
ほいっ、確認完了だ。
まとめ:相似な立方体の性質は3点セットで覚えよう!
相似な立体どうしの3つの性質を頭に入れとこう!
- 相似な立体同士は対応する線分の長さの比がすべて等しい
- 相似な立体同士の表面積比は相似比の2乗である
- 相似な立体同士の体積比は相似比の3乗である
表現を変えると、
相似な立体の相似比が m : nならば、
表面積比は m² : n²、
体積比は m³ : n³、
ご存じ、ロシア土産の定番「マトリョーシカ人形」。
1900年のパリ万博には出品されていたらしいね。
マトリョーシカ人形は一説では日本の「入れ子」に起源をもつという説や、ロシアの木工品だとか、諸説あるでござる。
相似な立体のどうしの性質を面白おかしく記憶にとどめてもらうために、ご出演願ったよ。

それじゃあな!
Dr.リード


