連立方程式の解き方はよくわからん！？
連立方程式の解き方には2つある。
それは、
- 加減法
- 代入法
だったね。
連立方程式の解き方が2つもあって便利・・・
って思うじゃん？。
だけれども、
「加減法・代入法」のどっちを選んだらいいのかわからない
って戸惑っちゃうことが多いんだ。
今日は、そんな迷いをぶっ放すために、
連立方程式の解き方（加減法or代入法）をみわけるコツ
を紹介していくよ。
すっきりしたいときに参考にしてみて。
〜もくじ〜
- 解き方を勉強する前に知っておきたいこと
- 解き方をみわける2つのコツ
連立方程式の解き方の○○割は「加減法」！？
まずやっぱり気になるのは、
加減法と代入法のどっちが多いのか？？
ということだよね。
平等に「50:50」なのか？？
もしくは、
超不平等に「1:99」なのか？？
じつは、これは経験上の話になるんだけど、
連立方程式の約90%が「加減法」を使っているんだ。
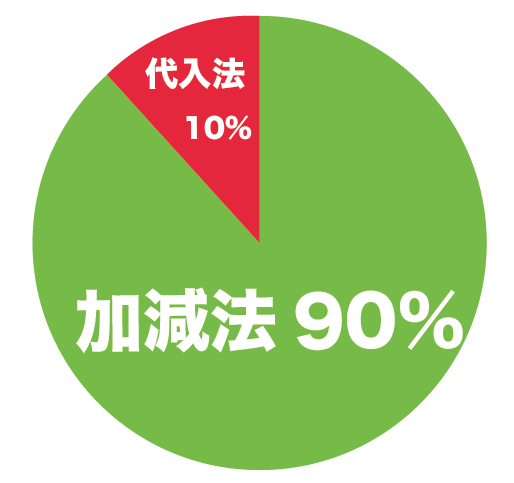
つまり、
「代入法」を使うときってめずらしいんだ。
「代入法」ってめんどうだからね。 使いたくないのは当然のことさ。
「加減法」を使ったほうが簡単に解ける問題が多いんだよ。
連立方程式の解き方をみわける2つのコツ
連立方程式の解き方（加減法or代入法）を見分けるコツは、
代入法で解く特殊なケースを覚える
ってことさ。
これを覚えちゃえば、
特殊なケースに出くわしたら「代入法」、
ソレ以外は「加減法」で解けるよね！
代入法を使う特別なケースってつぎの2つのときが多いよ。
ケース1. 文字が片方によっている問題
連立方程式の式で、
文字が片方によっている連立方程式
は代入法で解いたほうが便利なんだ。
しかも、よっている文字の係数が1ならなお最高！
たとえば次のような連立方程式の問題のときだね。
例題1. つぎの連立方程式を解きなさい。
$$2x+3y=11$$
$$y = 5x$$
この問題では、2つ目の方程式では「y」が左辺によっているよね？？
こういう場合、
よっている文字をもう1つの方程式に代入するだけでいいから、
代入法のほうが簡単なんだよ！
ケース2. 「代入法で解きなさい」と問題文で指示されている場合
問題文で「代入法で」連立方程式を解きなさい！
って命令されているパターンだ。
このときは指示に逆らわず、「代入法」で連立方程式をといてあげよう。
数学のテストでは問題文の命令はゼッタイだからね。
逆らってもろくなことがない。
たとえば、つぎのような問題のケースだ。
例題2. つぎの連立方程式を、代入法で解きなさい
$$2x+3y = 11$$
$$5x-9y =90$$
このパターンの場合、
どんなに「加減法」を使いたくても「代入法」で解かなきゃいけない。
おそらく、
解答用紙に「計算式」をかけ！
って要求してくるだろうからね。
問題文の命令はゼッタイ！
その道が険しくても・・・・ね！
まとめ：連立方程式の解き方はたいてい「加減法」
連立方程式の解き方はだいたい「加減法」だよ。
困ったら加減法。
めんどかったら加減法。
迷ったら加減法。
いや、なんとなく加減法。
そんじゃねー
