連立方程式をグラフから攻略？？
こんにちは！この記事をかいているKenだよ。無駄に課金しちゃったね。
一次関数のグラフってむちゃくちゃ便利。
なんと。
なんと、だよ。
グラフを使えば、
連立方程式の解を求めることができるんだ。
連立方程式の解き方がわからなくても大丈夫。
ぶっちゃけどうにかなる。
これってすごくない？。
そこで今日は、
一次関数のグラフをつかって連立方程式の解を求める方法を、
3つのステップで解説していくよ。
よかったら参考にして。
一次関数のグラフから連立方程式の解を求める3ステップ
つぎの例題をといてみよう。
つぎの連立方程式を、グラフを使って解きなさい。
3x + y = 5
x + y = 3
つぎの3ステップでとけちゃうよ。
Step1. 方程式のグラフを2つかく！
方程式のグラフを2つかこう。
かき方を忘れたときは、
「方程式とグラフ」を復習してみてね。
例題の、
- 3x + y = 5
- x + y = 3
の2つの方程式をグラフにしてみると、こうなるね ↓↓
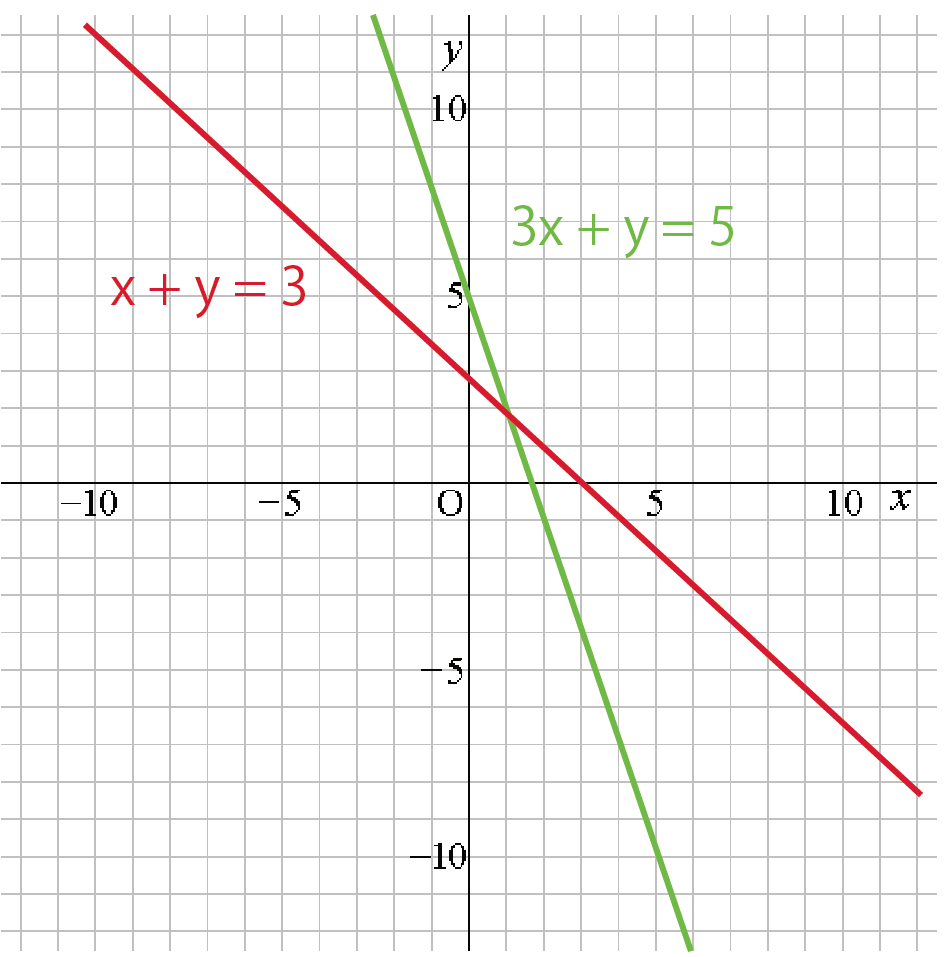
ここからが勝負さ！
Step2. 直線の交点をみつける！
グラフの交点をみつけてみよう。
よーくみつめてみて。
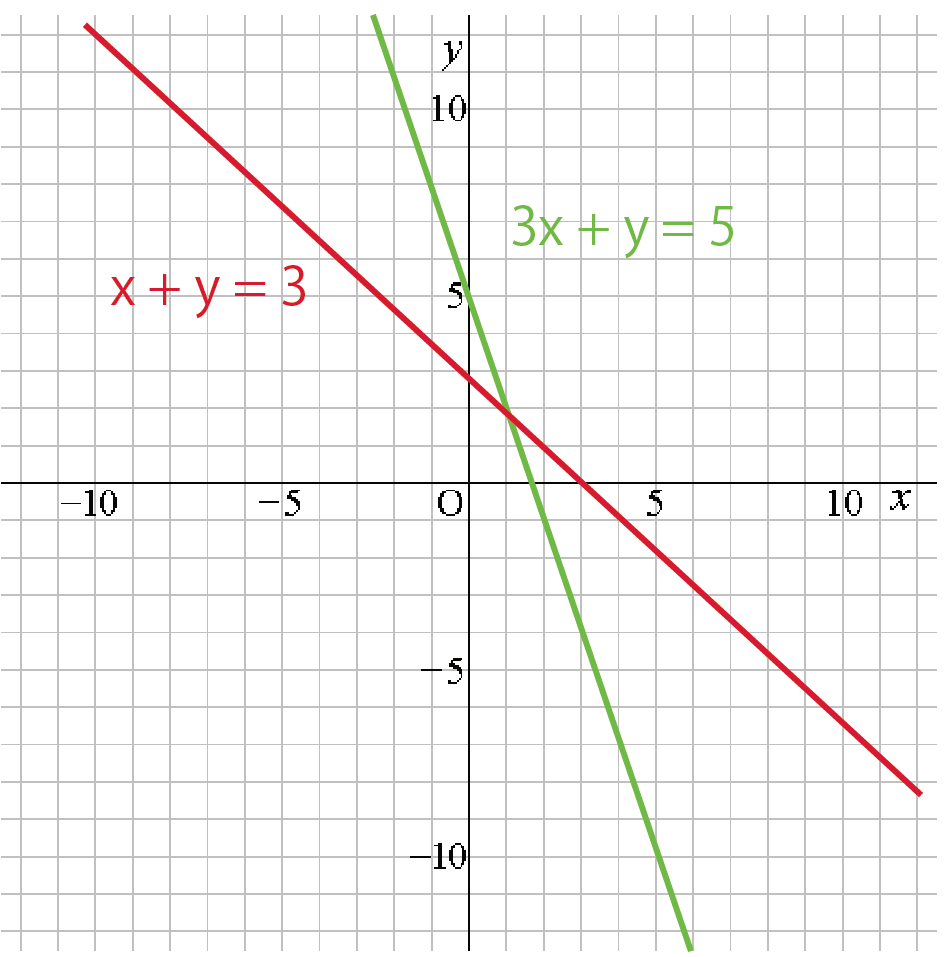
そう、
そうだ。
2つの直線がまじわっている点をみつければいいんだ。
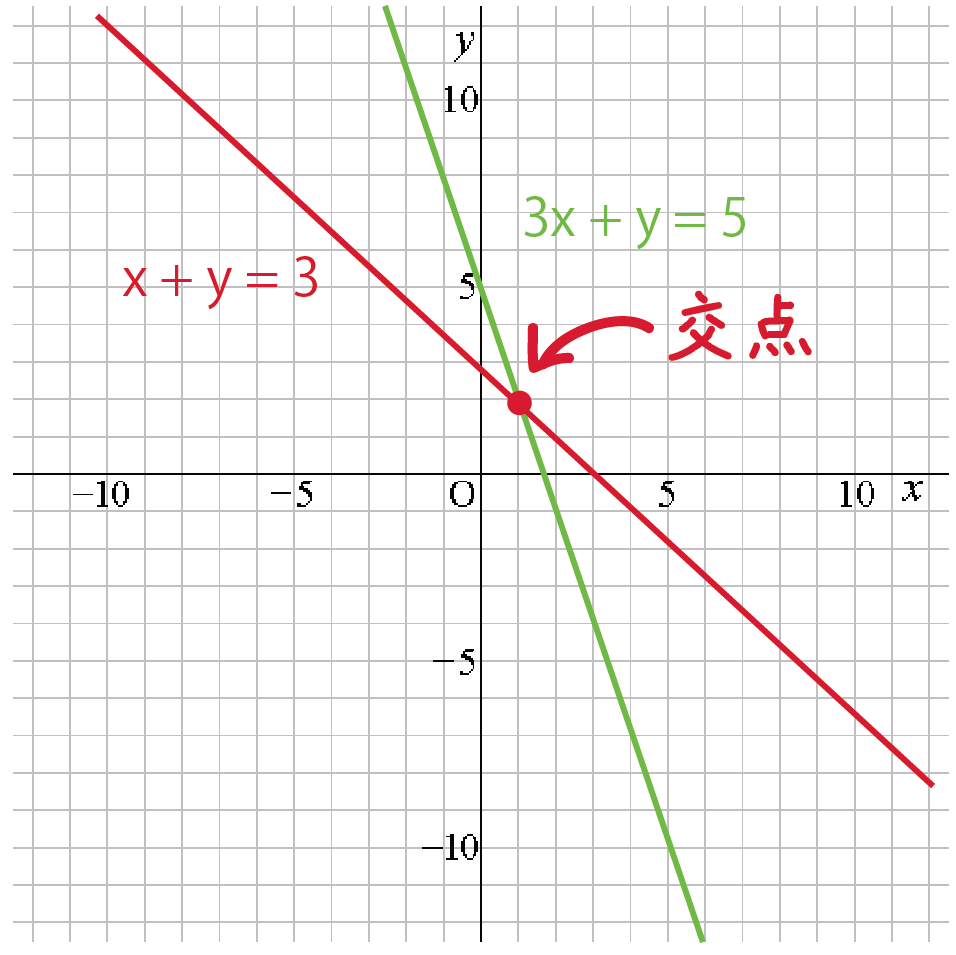
どう？
あったでしょ？？
Step3. 交点の座標を根性でよみとる！
最後に「交点の座標」をよみとろう。
座標がよめればこっちのものさ。
だって、
交点の座標 = 連立方程式の解
になるからね。
つまり、
- 交点のx座標 = 連立方程式のxの解
- 交点のy座標 = 連立方程式のyの解
になるんだ。
例題の交点をよみとってみると、
座標が（1, 2）であることがわかるね。
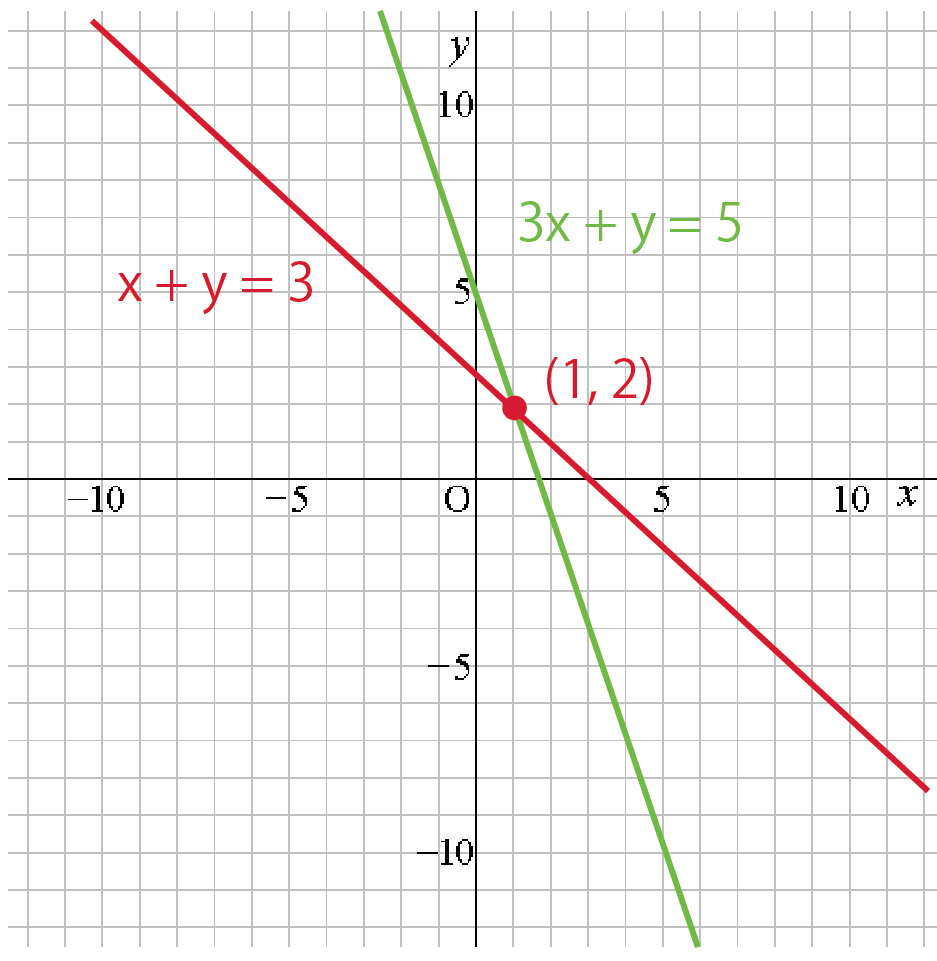
ってことは、
3x + y = 5
x + y = 12
の連立方程式の解は、
- x = 1
- y = 2
になるんだ。
やったね。
連立方程式の解き方を知らなくてもとけちゃった！てへ・・・
ってわけさ。
連立方程式が苦手なヤツにはこの方法haオススメだよ。
まとめ：連立方程式はグラフを使えばビュジュアルに解ける！
グラフをかくだけで連立方程式がとけるんだ。
つまり、
見た目（ビジュアル）だけでとけちゃうんだ。
むっちゃ便利でしょw？
たまにテストにでてくるから、よーく復習しておいてね。
そんじゃねー
Ken
