直方体の対角線の長さの求め方の公式だって！？
こんにちは！ぺーたーだよ。
三平方の定理を使うと、
直方体の対角線の長さの公式を導けるって知ってた？？
実は、対角線の長さには次の公式があるんだ。
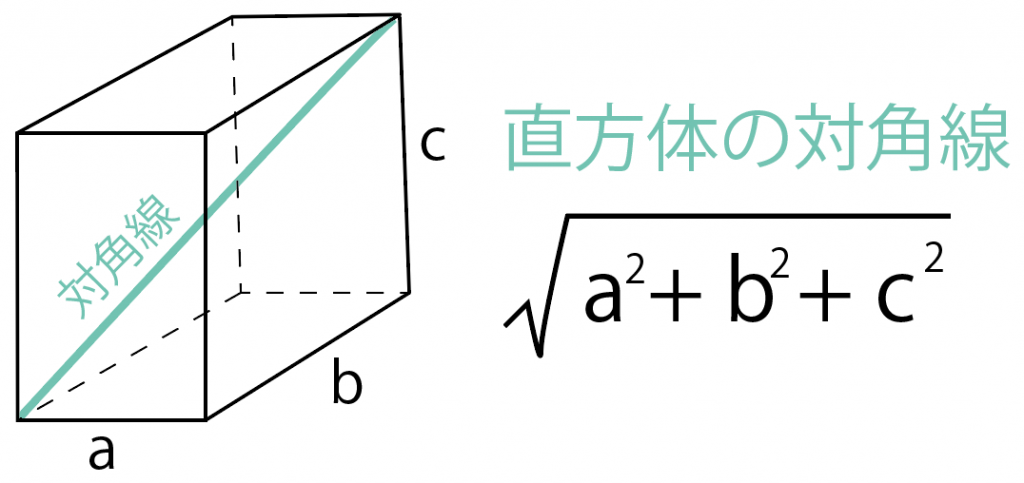
直方体のそれぞれの長さを、
- 縦：a
- 横：b
- 高さ: c
とすると、対角線の長さは、
√（a² + b² + c²）
になるよ。
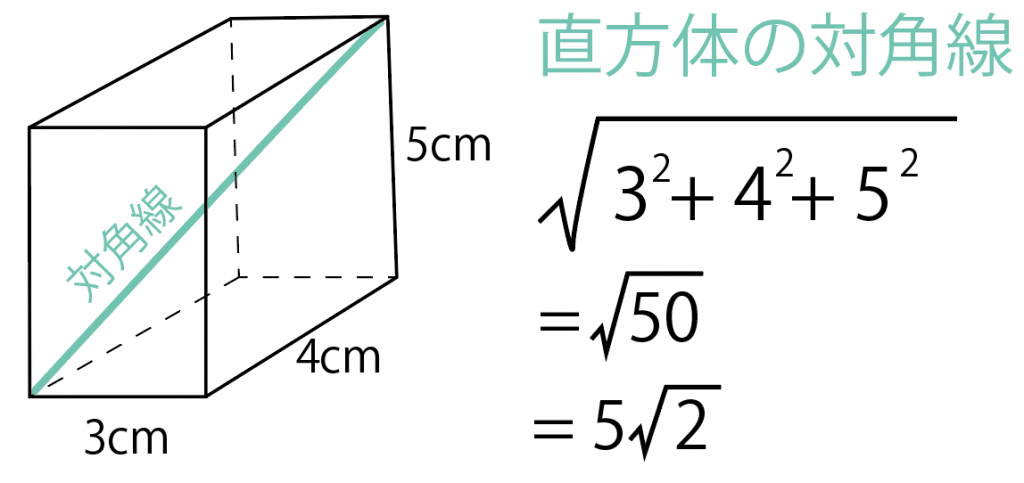
たとえば、
- 縦：3 cm
- 横：4 cm
- 高さ: 5 cm
の直方体があったとしよう。
こいつに直方体の対角線の公式を使ってやると、
対角線
= √（a² + b² + c²）
=√（3² + 4² + 5²）
= 5√2
になる。
どう？？
すぐに直方体の対角線の長さ求められたでしょ？？
でもね、公式を使うときには、
なぜその公式が使えるのか？？
を知っておくといいよ。
公式を忘れても大丈夫なようにね。
だから今日は最後に、
公式を使わずに直方体の対角線を求めてみよう。
直方体の対角線の長さの求め方がわかる2ステップ
さっそく、公式なしで直方体の対角線の長さを出してみようか。
- 縦：3 cm
- 横：4 cm
- 高さ: 5 cm
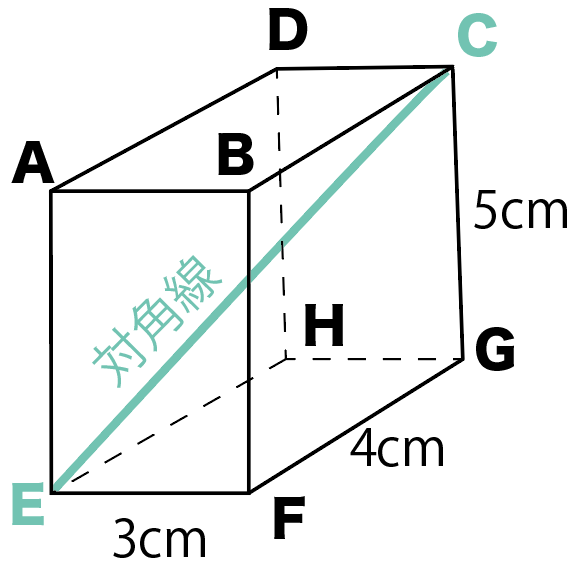
この問題では、対角線ECを求めてみよう。
Step1. 底面の対角線を引く
まず最初は、
底面の対角線を引いてみよう。
なんでそんなのひかなきゃいけないの？
って思うかもしれないけど、
その理由はあとでわかるからちょっとがまんしてね！
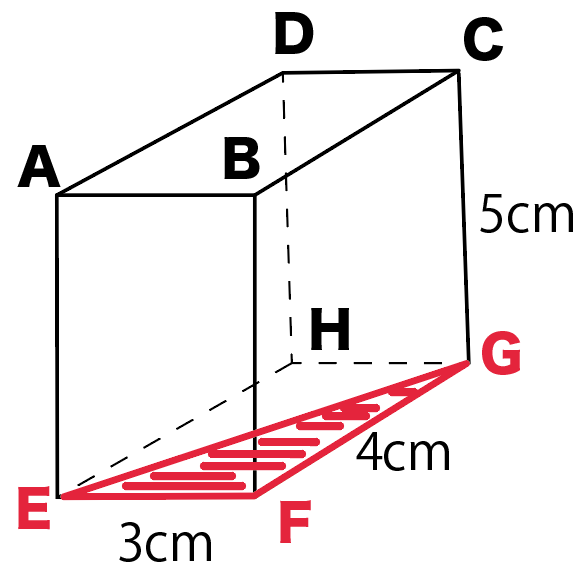
底面に対角線をひくとこうなるね。
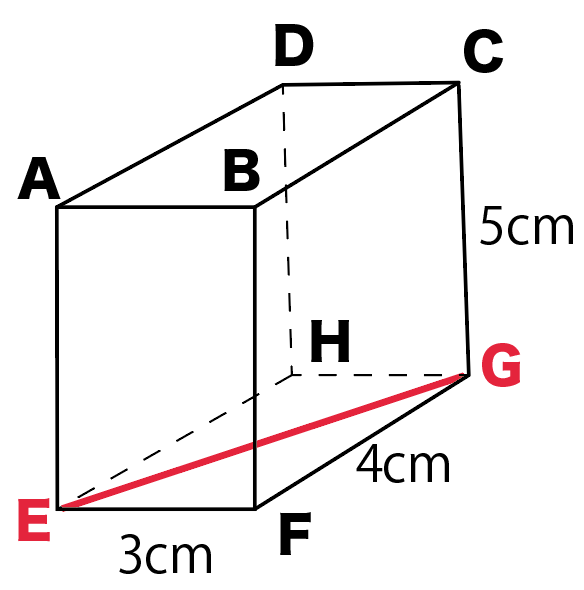
対角線ECを求めるために、
底面の対角線はEG
を引くってことね。
Step2. 底面の対角線の長さを求める
次は、底面の対角線の長さを計算してみよう。
えっ。
どうやって出すのかって？？
こういうときは、
底面にできた三角形に注目してみて。
さっきの直方体でいうと、
△EFG
だね。
この三角形は上から見るとわかると思うけど、
直角三角形になってるよね。
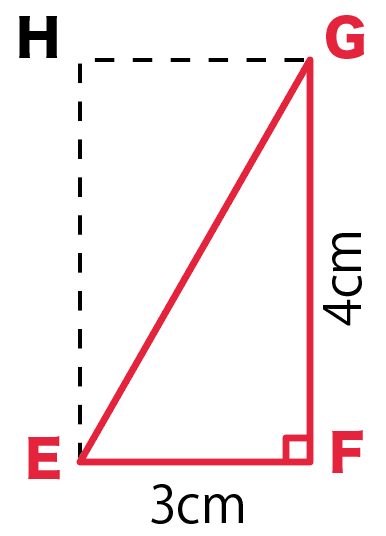
てことは、
三平方の定理で「斜辺EGの長さ」を求めることができるんだ。
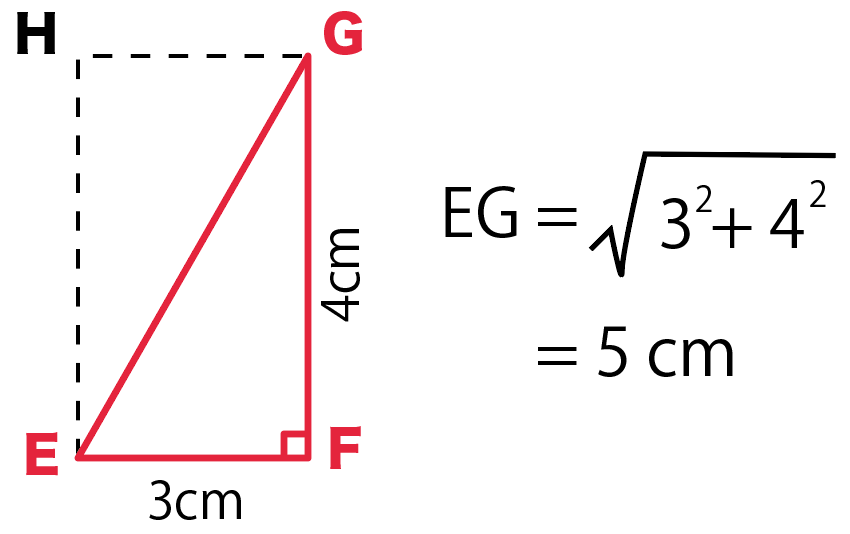
三平方の定理を使ってやると、
EG² = EF² + FG²
EG² = 3² + 4²
EG = 5 cm
になるね。
Step3. 直方体の対角線の長さを求める！
いよいよ本題の直方体の対角線の長さを求めるよ。
まず、求めたい直方体の対角線をさっきの図に書き込んでみよう。
対角線を書き込んだことで、また新しい三角形ができるよね？？
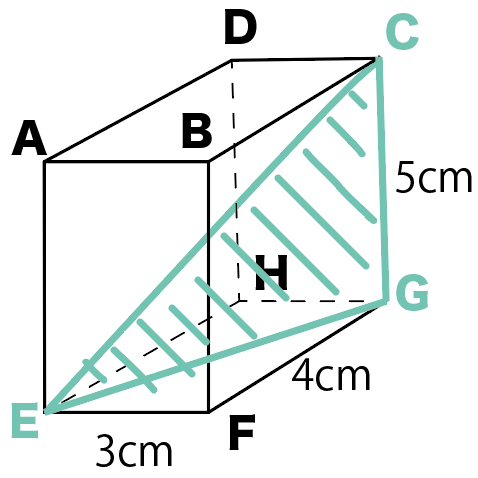
直方体の高さの辺と、底面の対角線でできる直角三角形ECGだ。
この三角形を取り出すと下みたいになるよ。
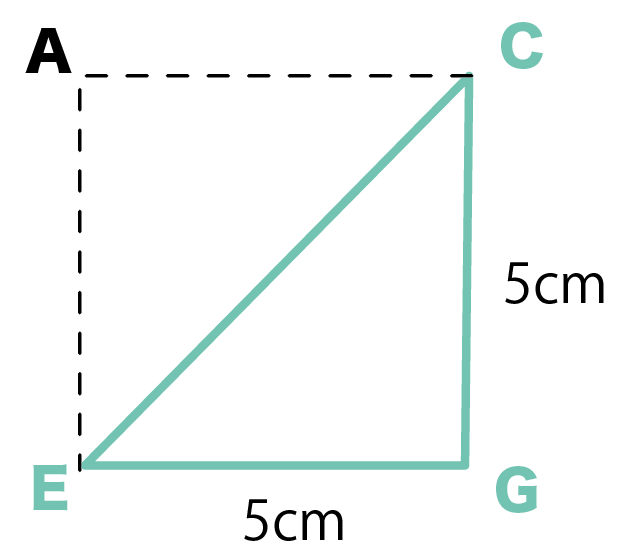
ここで、さっき求めた底面の対角線を使うんだ。
底面の対角線EGは5㎝だったね。
こいつを先に出しておかないと、うまく式が立てられず、計算できないんだ。
だから、底面の対角線を求めておくのはとっても大事ってわけ！
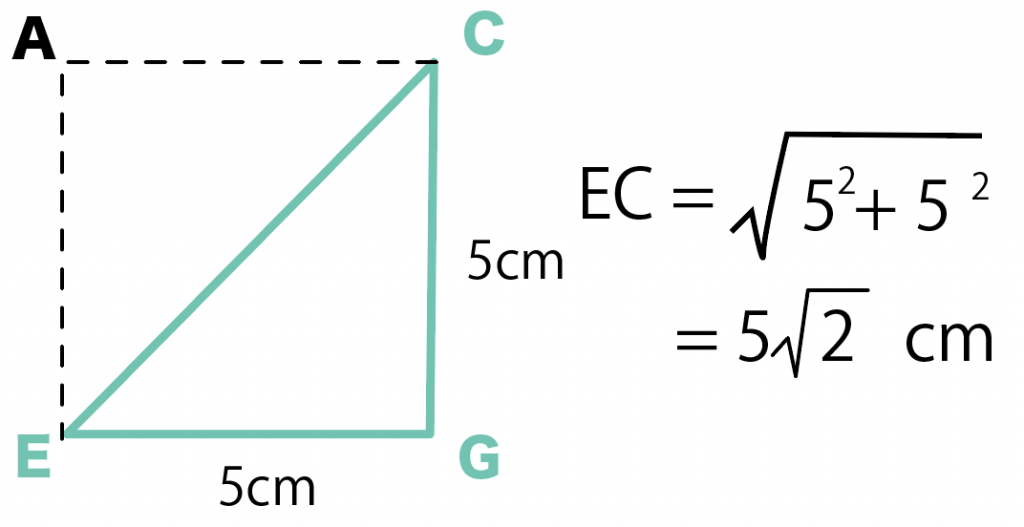
さっきと同じように三平方の定理を使うと、斜辺 ECの長さは、
EC² = CG² + FG²
EC² = 5² + 5²
EC = 5√2 cm
になるね。
つまり、
この直方体の対角線の長さは「5√2 cm」になるってわけ！
まとめ：底面の対角線を求めてから、直方体の対角線！
直方体の対角線の求め方はわかったかな？
- 底面の対角線の長さを求める
- 直方体の対角線の長さを求める
の2ステップでオッケー。
都合のいい直角三角形を見つけて、三平方の定理を使えれば全く問題ないね。
じゃあ、今日はここまでにしようか。
またね！お疲れさま！
ペーター
