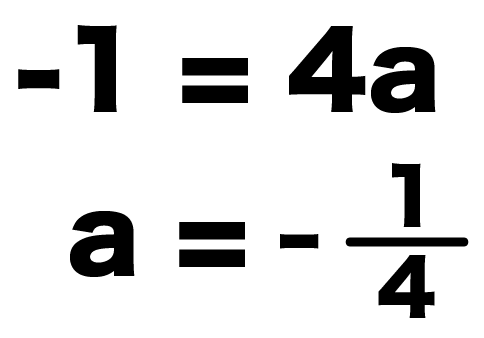二次関数y=ax2のグラフから式を読み取る？！
こんにちは！この記事をかいているKenだよ。ジンジャーは心にきくね。
中3数学では、
二次関数y=ax2を勉強していくよ。
ここではあろうことか、いろんな問題が出題される。
二次関数の比例定数を求める問題とか、
グラフをかく問題とか、
xとyの変域を求める問題とかね。
もう、ほんとたくさん。
そんな中でもとっつきやすいのが、
y=ax2のグラフから関数の式を読み取る問題
だ。
手頃でしれっと解けちゃうから、得点源になるはず。
この記事でしっかりマスターしておこう。
二次関数y=ax2のグラフから式を読み取る問題の解き方
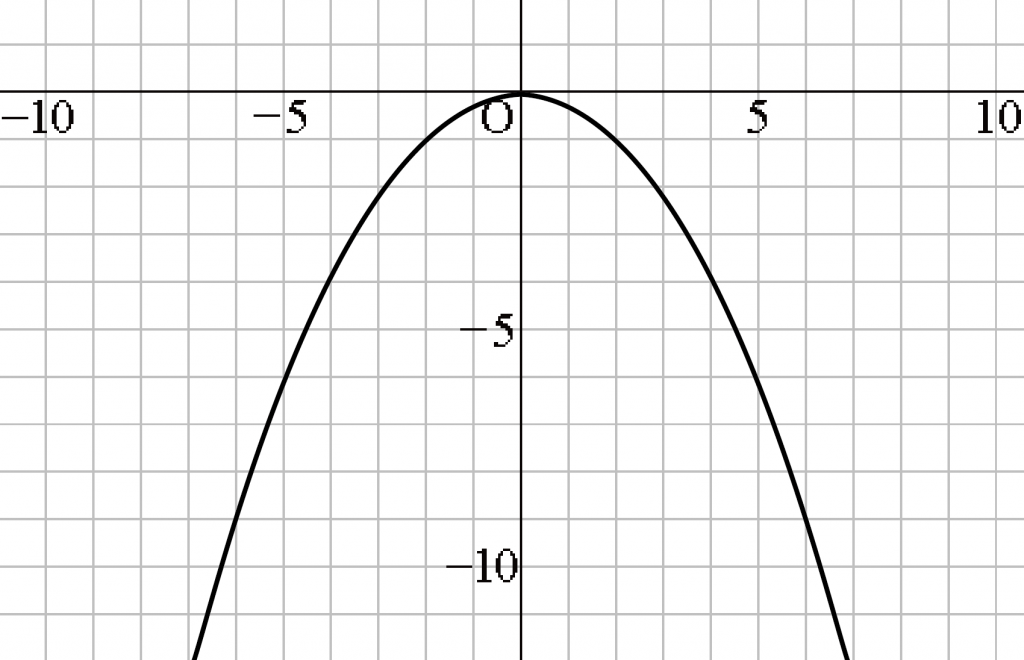
たとえばつぎのような問題だ。
つぎの曲線はy=ax2のグラフです。この関数の式を求めなさい。
この手の問題は3ステップでとけちゃうよ。
- x・y座標が正確に読み取れる点をさがす
- y = ax2に座標を代入
- 一次方程式を解く
Step1.「 x・y座標が読み取れる点」をさがす
まず、
x・y座標が正確に読み取れる点
をさがしてみよう。
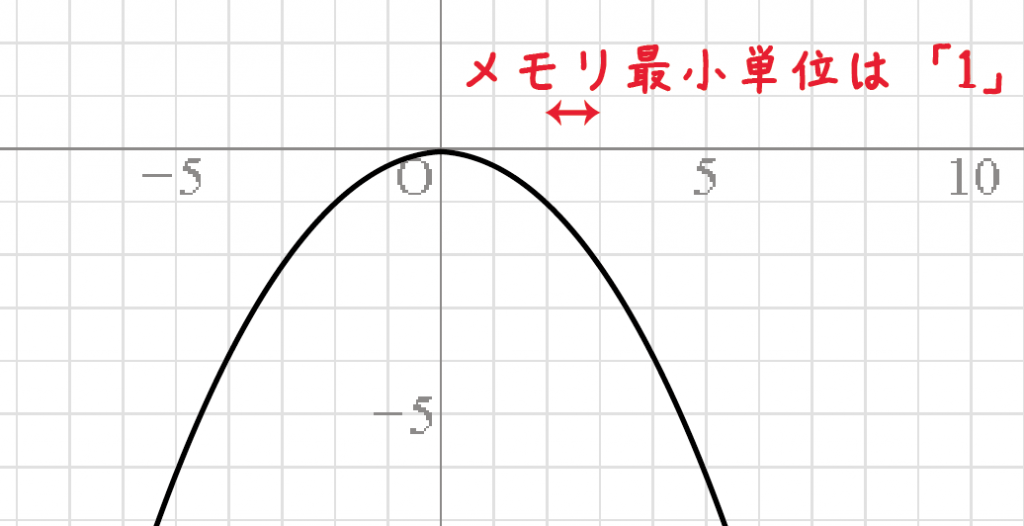
もし、座標のメモリの単位が「1」だとしたら、
x・y座標がともに整数になってる点をさがせばいいのさ。
例題のメモリの単位も「1」だよね？？
ってことは、xとyの座標が整数の点をさがせばいい。
よーく目をこらしてみてみると、
・・・・・・・・・・・
はっ！
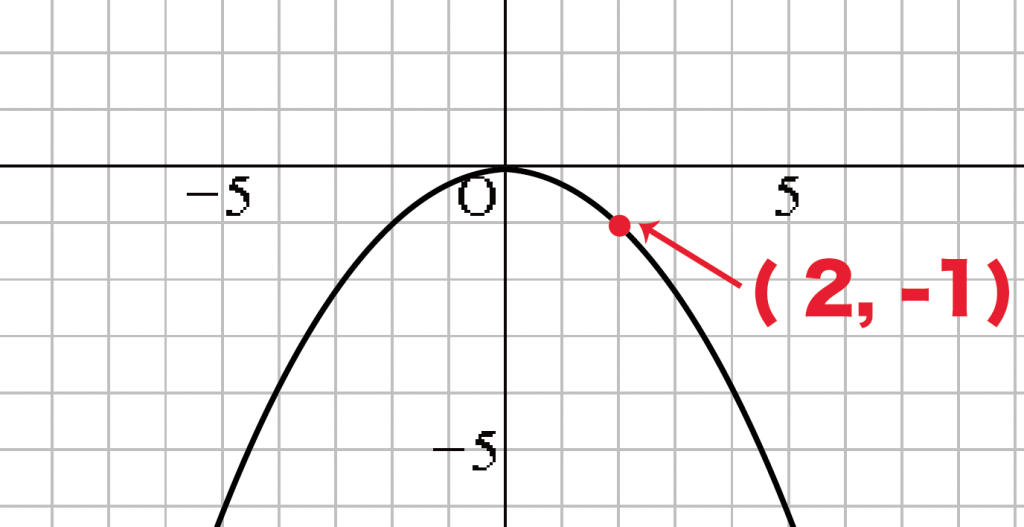
この放物線、
（2, -1）
とおってねえ？
こんなかんじで、xとyのメモリの交点を通っていて、
座標を読み取れる点をさがせばいいのさ。
Step2. 「y = ax2」に座標を代入
さっき読み取ったx、y座標を二次関数y=ax2に代入しよう。
- x 座標 ⇒ xに代入
- y 座標 ⇒ yに代入
っていったかんじで代入してみて。
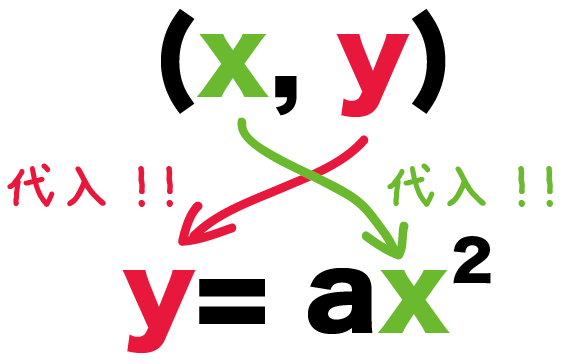
練習問題では、
- x 座標 ：2
- y 座標 ：-1
になってたよね？？
この座標たちをy= ax2に代入してみると、
-1 = a × (2)^2
-1 = 4a
になる。
Step3. 一次方程式を解く
あとは一次方程式を解くだけ。
xとyの座標を二次関数y=ax2に代入すると、
aに関する1次方程式ができるはず。
こいつを方程式の解き方通りにといてやればいいのよ。
練習問題でのこった一次方程式は、
-1 = 4a
だね？？
こいつをaについて解いてやると、
a = -4分の1
になる。
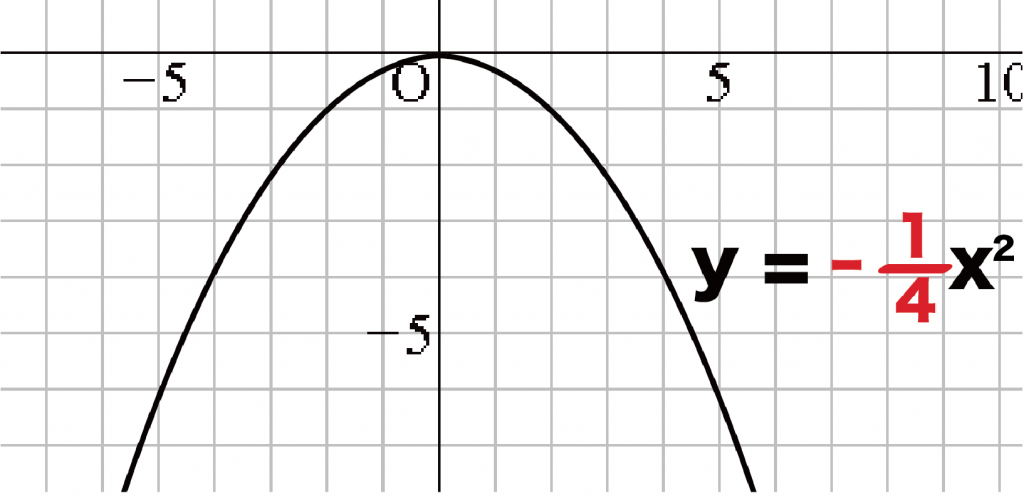
よって、このグラフの二次関数y= ax2の式は、
y = -4分の1 x^2
になるね。
おめでとう！
これでy =ax2のグラフから式を読み取れたね。
二次関数y=ax2のグラフから式を読み取るには目をこらせ！
二次関数y=ax2のグラフから式を読み取れるようになったかな？？
解き方の最大のコツは、
座標を正確に読み取ること。
これにつきる。
ここで間違えると、一次方程式も意味をなさなくなっちゃうからね。
遠視の人はめがねをかけてでもいいから、
正確に座標をゲットしてみよう。
そんじゃねー
Ken
