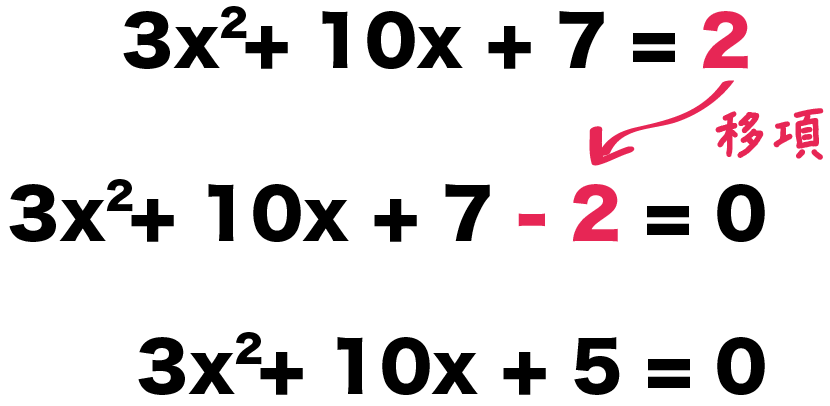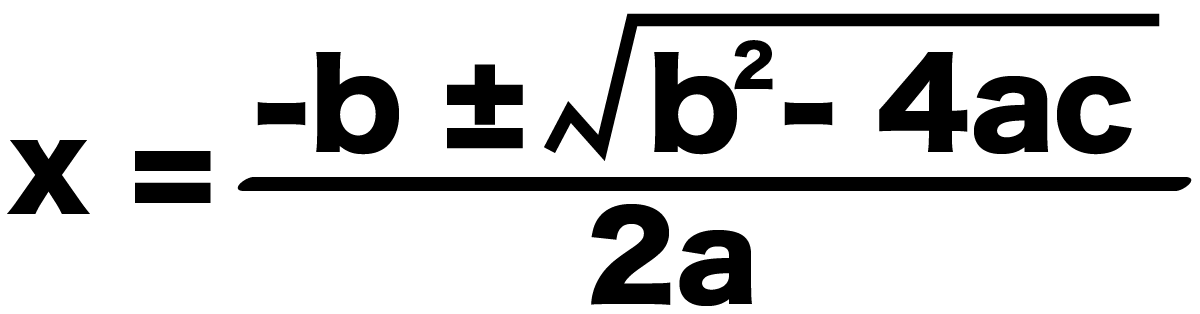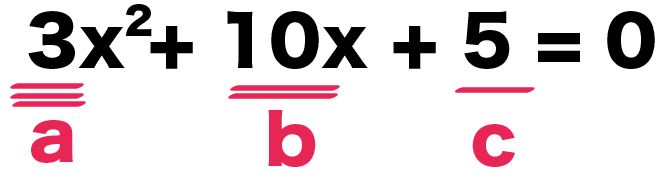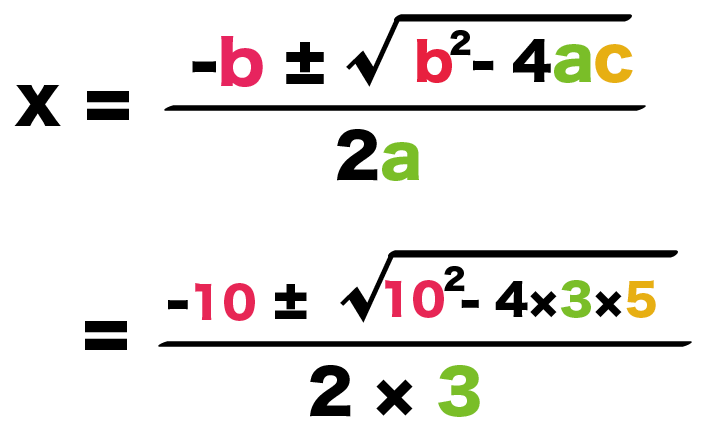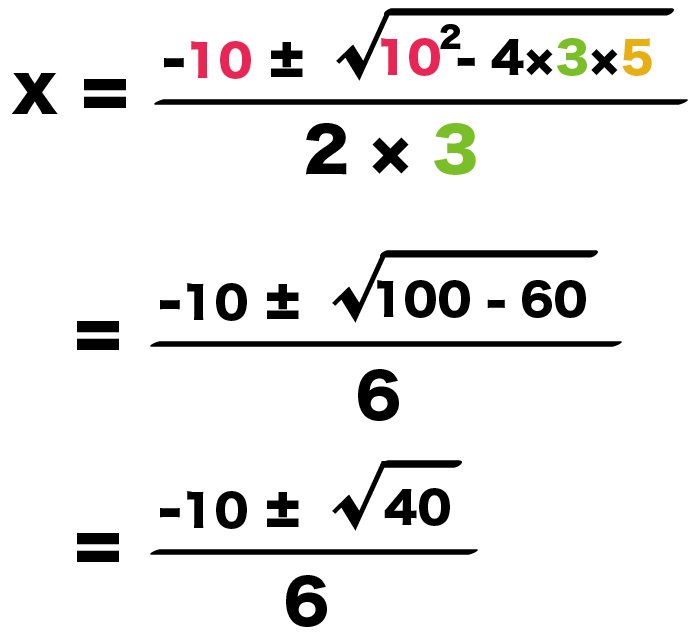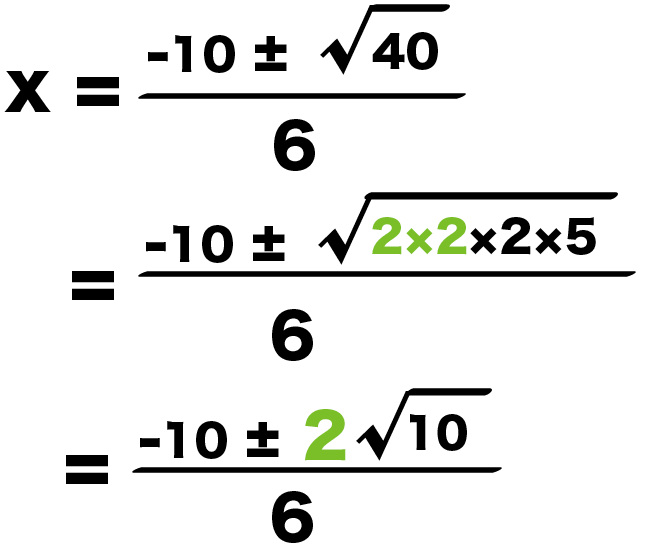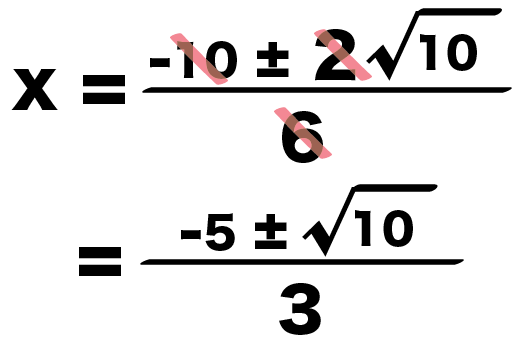【簡単計算】解の公式の問題のやり方がわかる4つのステップ
解の公式の計算問題のやり方??
はろー、犬飼ふゆだよ。
2次方程式ってテストに必ずでてくるよね??
解き方を覚えて損はない!って断言できちゃうよ。
因数分解をつかっても解けるんだけど、どうにもならない場合に
「任せとけ! 絶対に解けるから!」
っていう強い味方がいるの知ってたかな?
それが
「解の公式」
なんだ。
高得点を狙いたいなら絶対にCheckだよー。
今日はこの、
解の公式の計算問題のやり方をわかりやすく解説してみたよ。
解の公式の計算問題のやり方がわかる4ステップ
さっそく解の公式の計算を解説していくよ。
つぎの練習問題をといてみよう。
解の公式なら4ステップでとけちゃうんだよ。
- 移項する
- 公式をつかう
- ルートを簡単にする
- 約分する
Step1. 「ax2+bx+c=0」という形にする
移項して右辺をゼロにしてみよう。
最終的に、
ax²+bx+c=0
っていう形にもってけばOKだよ。
練習問題の二次方程式では、右辺に「2」が残ってるね??
3x²+10x+7 = 2
こいつを左辺に移項してやると、
3x²+10x+7 = 2
3x²+10x+7 – 2 = 0
3x²+10x+5 = 0
になるね!
Step2. 解の公式に係数を代入する
さてと、因数分解で二次方程式とくかな・・・・
え!因数分解できない!!
じゃあ共通因数でくくるかな・・・・
あれ!?共通因数でくくれない!!
・・・・・・・・・・
そんなときに使えるのが解の公式だったよね??
解の公式を簡単におさらいしておくと、
二次方程式 ax2+bx+c=0の解xは、
x = {-b±√(b² – 4ac)}/2a
になるんだったね??
これマジ重要。
紙に書いて机のそばに貼っておきたいくらい。
面倒でも覚える価値あるよ。
練習問題の2次方程式は、
3x²+10x+5 = 0
になったよね??
ってことは、解の公式の各係数は、
- a = 3
- b = 10
- c = 5
になるね!
この3つの値を解の公式に代入してやると、
x = {-b±√(b² – 4ac)}/2a
= {-10 ± √(10² -4×3×5)}/2/3
になる。
Step3. ルートの中身を簡単にする
つぎはルートの中身を簡単にしよう。
さっきの計算では、
x = {-10 ± √(10² -4×3×5)}/2/3
になったよね??
この分子のルートの中身を計算してやると、
x = {-10 ± √(100-60)}/6
= {-10 ± √40}/6
になるね。
ふう。。。終わった。。。。
あ、ちょい待って。
ルートの中身の40って素因数分解すると2×2×2×5だね。
2×2がダブってるから、ルートの外に出しちゃおっか。
x = {-10 ± √40}/6
= {-10 ± 2√5}/6
Step4. 約分する
最後は約分できるか確認しよう。
練習問題でも約分できそう。
だって、分母と分子が両方2でわれるもん。
分子のぜんぶの項を2で割るように注意しようね。
さっそく約分してやると、
x = {-10 ± 2√5}/6
={-5 ± √5}/3
になるね。
どうかな?
むずかしそうだけど、ちゃんと解が出たでしょう?
解の公式すっごい便利だからぜひぜひ! 覚えておいてね。
まとめ:解の公式の計算問題は慎重にとけば大丈夫
解の公式はほんとうに便利。
因数分解の公式もつかえないし、共通因数でもくくれない。
そんなときに解の公式をつかってみてね。
たくさん使って問題に慣れていこう。
じゃあねー
犬飼ふゆ